北交大附中2005-2006学年度第一学期高三年级质量检测
数 学 试 题
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
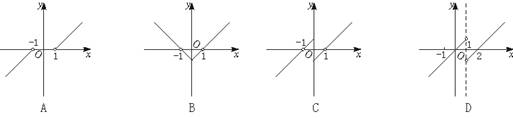
1.奇函数y=f(x)(x≠0),当x∈(0,+∞)时,f(x)=x-1,则函数f(x-1)的图象为( )
2. 设a>b>c,且![]() ,则n的最大值为
( )
,则n的最大值为
( )
A.2 B.3 C.4 D.5
3.命题甲:![]() 或
或![]() ;命题乙:
;命题乙:![]() ,则
( )
,则
( )
A.甲是乙的充分非必要条件; B.甲是乙的必要非充分条件;
C. 甲是乙的充要条件; D.甲既不是乙的充分条件,也不是乙的必要条件.
4.函数![]() 是 ( )
是 ( )
A.周期为![]() 的奇函数
B. 周期为
的奇函数
B. 周期为![]() 的偶函数
的偶函数
C.周期为2![]() 的奇函数
D。周期为2
的奇函数
D。周期为2![]() 的偶函数
的偶函数
5.双曲线的焦点在y轴上,且它的一个焦点在直线5x-2y+20=0上,两焦点关于原点对称,![]() ,则此双曲线的方程是( )
,则此双曲线的方程是( )
A. ![]() B.
B. ![]()
C. ![]()
D.
D. ![]()
6. 函数![]() ,
,![]() ,当
,当![]() 时,
时,![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是 ( )
的取值范围是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D。
D。![]()
7. 已知函数![]() 的定义域为R,它的反函数为
的定义域为R,它的反函数为![]() ,如果
,如果![]() 与
与![]() 互为反函数且
互为反函数且![]() 。(
。(![]() 为非零常数)则
为非零常数)则![]() 的值为 ( )
的值为 ( )
A.![]() B。0
C。
B。0
C。![]() D。
D。![]()
8.数列![]() 满足
满足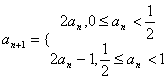 ,若
,若![]() ,则
,则![]() 的值为( )
的值为( )
A.![]() B.
B. ![]() C.
C. ![]() D。
D。![]()
9.设直线![]() 的倾斜角为
的倾斜角为![]() ,则该直线关于直线
,则该直线关于直线![]() (
(![]() )对称的直线的倾斜角为 ( )
)对称的直线的倾斜角为 ( )
A.![]() B.
B. ![]() C.
C. ![]() D。
D。![]()
10. 若对于任意的![]() ,函数
,函数![]() ,
,![]() 满足
满足![]() ,则称在
,则称在![]() 上
上![]() 可以替代
可以替代![]() 。若
。若![]() ,则下列函数中可以在[4,16]替代
,则下列函数中可以在[4,16]替代![]() 是 ( )
是 ( )
A.![]() B.
B. ![]() C.
C. ![]() D。
D。![]()
11.已知x,y满足不等式组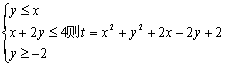 的最小值为 ( )
的最小值为 ( )
A.![]() B.2 C.3 D.
B.2 C.3 D.![]()
12.ABCD-A1B1C1D1单位正方体,黑白两个蚂蚁从点A出发沿棱向前爬行,每走完一条棱称为“走完一段”。白蚂蚁爬地的路线是AA1→A1D1→……,黑蚂蚁爬行的路线是AB→BB1→……,它们都遵循如下规则:所爬行的第i+2与第i段所在直线必须是异面直线(其中i是自然数)。设白,黑蚂蚁都走完2005段后各停止在正方体的某个顶点处,这时黑,白两蚂蚁的距离是 ( )
A、1
B、![]() C、
C、![]() D、0
D、0
高三大联考模拟考试数学试卷
命题人:邓永生
第Ⅱ卷(非选择题 共90分)
二、 填空题:(本大题共4小题,每小题4分,共16分,把答案填在题目中的横线上。)
13.不等式![]() 的解集是
。
的解集是
。
14. 把函数y=2x2-4x+5的图象按向量a平移,得到y=2x2的图象,且a⊥b,c=(1,-1),b•c=4,则b=___________
15.已知函数![]() 满足:
满足:![]() ,
,![]() ,则
,则
![]() +
+![]() +
+![]() +
+![]() +
+![]() = 。
= 。
16.在等比数列![]() 中,若
中,若![]() ,则有等式
,则有等式![]() ,
,![]() 。类比上述性质,相应的在等差数列
。类比上述性质,相应的在等差数列![]() 中,若
中,若![]() ,则有等式
成立。
,则有等式
成立。
三、 解答题:本大题共6小题,共74分,要求写出必要的解答过程,否者不能得分。
17. (本题满分12分)已知集合![]() ,集合
,集合![]() 满足
满足![]() ,求实数
,求实数![]() 的值。
的值。
18.(本小题12分) 已知![]()
![]() ,(1)若
,(1)若![]() ,求
,求![]() 的最小值;(2)若不等式
的最小值;(2)若不等式![]() 对于一切
对于一切![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围。
的取值范围。
19.(本题满分12分)已知向量 a=(1,1),b=(1,0),c满足a![]() c=0且a=b,b
c=0且a=b,b![]() c>0.
c>0.
1).求向量c;2)若映射![]()
![]() a+
a+![]() c,
c,
①求映射![]() 下(1,2)的原象;
下(1,2)的原象;
②若将(![]() )看作点的坐标,问是否存在直线
)看作点的坐标,问是否存在直线![]() 使得直线上的任一点在映射
使得直线上的任一点在映射![]() 的作用下点仍在直线上,若存在求出直线
的作用下点仍在直线上,若存在求出直线![]() 的方程,否则说明理由。
的方程,否则说明理由。
20.(本小题12分)学校餐厅每天供应1000名学生用餐,每星期一有A、B两样特色菜可供选择(每个学生都将从二者中选一),调查资料表明,凡是在本周星期一选A菜的,下周星期一会有20%改选B,而选B菜的,下周星期一则有30%改选A,若用A![]() 、B
、B![]() 分别表示在第n个星期一选A、B菜的人数。
分别表示在第n个星期一选A、B菜的人数。
(1)试以A![]() 表示A
表示A![]() ;(2)若A
;(2)若A![]() =200,求{A
=200,求{A![]() }的通项公式;
}的通项公式;
(3)问第n个星期一时,选A与选B的人数相等?
21.(本小题满分12分)设![]() ,
,![]() 分别是直线
分别是直线![]() 和
和![]() 上的动点,(
上的动点,(![]() ,
,![]() 两点的纵坐标符号相同),O是坐标原点,且△
两点的纵坐标符号相同),O是坐标原点,且△![]() 的面积为9。①求线段
的面积为9。①求线段![]() 的最小值;②求线段
的最小值;②求线段![]() 的中点M的轨迹方程;③设点
的中点M的轨迹方程;③设点![]() 是直线
是直线![]() 上的点,且点
上的点,且点![]() 分有向线段
分有向线段![]() 所成的比是
所成的比是![]() (
(![]() ),求点
),求点![]() 的轨迹方程。
的轨迹方程。
22.(本题满分14分)对于函数![]() ,若存在
,若存在![]() ,使
,使![]() 成立,则称点
成立,则称点![]() 为函数的不动点。(1)已知函数
为函数的不动点。(1)已知函数![]() 有不动点(1,1)和(-3,-3)求
有不动点(1,1)和(-3,-3)求![]() 与
与![]() 的值;(2)若对于任意实数
的值;(2)若对于任意实数![]() ,函数
,函数![]() 总有两个相异的不动点,求
总有两个相异的不动点,求![]() 的取值范围;(3)若定义在实数集R上的奇函数
的取值范围;(3)若定义在实数集R上的奇函数![]() 存在(有限的)
存在(有限的)![]() 个不动点,求证:
个不动点,求证:![]() 必为奇数。
必为奇数。
参考答案
一,选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | C | B | C | A | D | B | C | D | C | D | B |
二,填空题
13.![]()
14.(3,-1)
15. 30
16.![]()
三解答题:
17.解:∵![]() ;
;![]() ;
;![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]()
18.解:(1)![]()
![]() ,
,
∴![]() ,等号当且仅当
,等号当且仅当![]() ,即
,即![]() 时取得。∴
时取得。∴![]() 的最小值为
的最小值为![]() 。
。
(2)不等式即为![]() ,也就是
,也就是![]() ,
,
令![]() ,则
,则![]() 在
在![]() 上恒成立,∴
上恒成立,∴![]() ,解得
,解得![]() 。
。
19.解:1)设![]() ,由题意得:{
,由题意得:{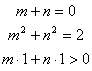 解得{
解得{![]() 。
。
∴c=![]() .
.
2) ①由题意![]() ,得
,得![]() ,解得:{
,解得:{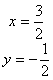
∴(1,2)的原象是![]() 。
。
②假设存在直线![]() 适合题设,平行于坐标轴的直线显然不适合。设所求的直线方程为:
适合题设,平行于坐标轴的直线显然不适合。设所求的直线方程为:
![]() ,在直线上任取一点
,在直线上任取一点![]() ,经过映射
,经过映射![]() 的作用得点Q:
的作用得点Q:![]() 仍在该直线上,∴
仍在该直线上,∴![]() ,即
,即![]() 。
。
当![]() 时,
时,![]() 无解,故这样的直线不存在。
无解,故这样的直线不存在。
当![]() 时,
时,![]() 即
即![]() ,解得:
,解得:![]() 。故这样的直线
。故这样的直线![]() 存在,其方程为
存在,其方程为![]() 或
或![]()
20.解:(1)由题可知,![]() ,又
,又![]() ;
;
所以整理得:![]() 。
。
(2)若A![]() =200,且
=200,且![]() ,则设
,则设![]() 则
则![]() ,
,
∴![]() 即{A
即{A![]() -600}可以看成是首项为-400,公比为
-600}可以看成是首项为-400,公比为![]() 的等比数列。
的等比数列。
∴![]() ;
;
(3)∵![]() ,又
,又![]() 则
则![]() , 由
, 由![]() 得
得![]() 。即第3个星期一时,选A与选B的人数相等。
。即第3个星期一时,选A与选B的人数相等。
21.解:(本题由2004年北京东城考题改编)①设![]() 和
和![]() ,
,![]()
则直线![]() 的方程为
的方程为 ![]() ;令
;令![]() 得
得![]() ;
;
∴S△![]() =
=![]()
![]()
![]() =
=![]() ,∴
,∴![]()
所以:![]() ,
,
当且仅当![]() 时
时![]() ;
;
②线段![]() 的中点M的轨迹方程为:
的中点M的轨迹方程为:![]() ;
;
③设点![]() 的坐标为
的坐标为![]() ,由点
,由点![]() 分分有向线段
分分有向线段![]() 所成的比是
所成的比是![]() (
(![]() )得:
)得:
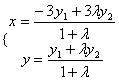 所以
所以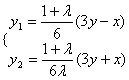
又![]() ,故点
,故点![]() 的轨迹方程为:
的轨迹方程为:![]() 。
。
22.解答:(1)由不动点的定义:![]() ,
,
∴![]() ,代入
,代入![]() 知
知![]() ,又由
,又由![]() 及
及![]() 知
知![]() 。
。
∴![]() ,
,![]() 。
。
(2)对任意实数![]() ,
,![]() 总有两个相异的不动点,即是对任意的实数
总有两个相异的不动点,即是对任意的实数![]() ,方程
,方程![]() 总有两个相异的实数根。
总有两个相异的实数根。
∴![]() 中
中![]() ,
,
即![]() 恒成立。故
恒成立。故![]() ,∴
,∴![]() 。
。
故当![]() 时,对任意的实数
时,对任意的实数![]() ,方程
,方程![]() 总有两个相异的不动点。
总有两个相异的不动点。
(3)![]() 是R上的奇函数,则
是R上的奇函数,则![]() ,∴(0,0)是函数
,∴(0,0)是函数![]() 的不动点。若
的不动点。若![]() 有异于(0,0)的不动点
有异于(0,0)的不动点![]() ,则
,则![]() 。
。
又![]() ,∴
,∴![]() 是函数
是函数![]() 的不动点。
的不动点。
∴![]() 有限个不动点除原点外,都是成对出现的,有
有限个不动点除原点外,都是成对出现的,有![]() 个(
个(![]() ),加上原点,共有
),加上原点,共有![]() 个。
个。