当前位置：首页 -高中数学试卷 - 高考数学试题 - 正文*

高考成都市高中毕业班摸底测数学文科

2014-5-11 0:13:17下载本试卷

成都市2006届高中毕业班摸底测试

数学(文科)

(全卷满分为150分，完成时间为120分钟)

第Ⅰ卷（选择题　共60分）

注意事项：

  1. 答第Ⅰ卷前，考生务必将自己的姓名、考号、考试科目用铅笔填写在答题卡上.
  2. 每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦擦干净后，再选涂其他答案，不能答在试题卷上.
  3. 考试结束，监考员将本试卷和答题卡一并收回.

参考公式：

如果事件A、B互斥，那么　　　　　　　　　　　　　　　　　　　　球的表面积公式

　　　P（A+B）=P（A）+P（B）　　　　　　　　　　　　　　　　　　　　 S=4πR2

　　　 如果事件A、B相互独立，那么　　　　　　　　　　　　　　　　　　其中R表示球的半径

　　　P（A·B）=P（A）·P（B）　　　　　　　　　　　　　　　　 球的体积公式

　　　 如果事件A在一次试验中发生的概率是P，　　　　　　　　　V=πR3

那么n次独立重复试验中恰好发生k次的概率　　　　　　　　　其中R表示球的半径

Pn(k)= CPk(1－P) n－k

一、选择题：本题共有12个小题，每小题5分，共60分;在每小题给出的四个选项中，只有一项是正确的，把正确的代号填在机读卡的指定位置上.

1.若集合A={-1,0,1}，集合B={1,2,3}，则集合A∪B应表示为

A.{1}　　　　 　 B.{-1,0}　　　　　　　　　C.{0,1,2,3}　　　　　 D.{0,-1,1,2,3}

2.已知sin的值为

　A.　　　　 B.-　　　　　C.　　　　　　D.

3.已知正项等比数列{}中，,则数列{}的公比为

A.　　　　B.2　　　　　　 C.±2　　　　　 D. ±

4．函数x的大致图象是

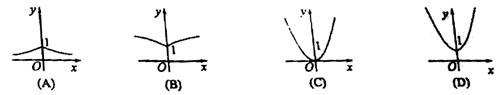
5.某交往式计算机有20个终端，这些终端由各个单位独立操作，使用率均为0.8，则20个终端中至少有一个没有使用的概率为

　A.0.220　　　　　　　B.0.820　　　　　C.1-0.820　　　　　　D.1-0.220

6.已知△中，=3，=4，且·＝－6，则△的面积是

A.6　　　　　　　　　　B.3　　　　　　　　 C.3　　　　　　　　　　　　　　　D.

7.已知椭圆的方程为2x2 +3y2=m(m>0),则此椭圆的离心率为

  A.　　　　　　　　　B.　　　　　　　　　C. 　　　　　　　　　　　 D.

8.若直线a∥平面α，则直线a与平面α内的直线的关系是

A.平面α内有且仅有一条直线与a平行

B.平面α内任意一条直线与直线a平行

C.平面α内与直线a共面的直线与直线a平行

D.以上都不对

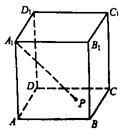
9.如图，P为正方体AC1的底面ABCD内任意一点，若A1P与棱A1A、A1B1、A1D1所成的角分别为α、β、γ，则sin2α+sin2β+sin2γ的值为

A.2　　　　　　　　　　　　　　　　　　　　　　　　　　　B.1

C. 0　　　　　　　　　　　　　　　　　　　　　　　　　　 D.随P的变化而变化

10.下列不等式中解集为实数集R的是

  A. x2+4x+4>0　　　　　　　　　　　　　　　　　　　　B.>0

C.　　　 　　　　　　　　　　　　　　　　　　　　D.x2-x+1>0

11.已知抛物线y2=4x及点A(1,1)，若过点A的直线被此抛物线截得的弦PQ恰以A为中点，则直线PQ的方程为

　A.4x-y-3=0　　　　　　　　B.2x-y+1=0　　　　　　C.4x-y+3=0　　　　　　　　　D.2x-y-1=0

12.若一系列函数的解析式相同，值域相同，但定义域不同，则称这些函数为“孪生函数”，那么函数解析式为y=2x2+1，值域为{5,19}的“孪生函数”共有

　A.10个　　　　　　　B.9个　　　　　　　　　　　　　C.8个　　　　　　　　　　　　　　　　 D.7个

第Ⅱ卷（非选择题　共90分）

二、填空题：(本大题共4小题，每小题5分，共20分)把答案填在题中横线上.

13.(x2-展开式中各项系数之和为　　　  .

14.直线y=-(x-1)被圆(x-1)2+(y+2)2=4所截得的弦长为　　　　　  .

15.双曲线3x2-4y2-12x+8y-4=0按向量平移后的双曲线方程为，则平移向量=　　　　　　　  .

16.给出以下命题：①已知命题p、q，若“p或q”为真，则“p且q”为假；②已知平面α、β均垂直于平面γ，α∩γ=a,β∩γ=b，则α⊥β的充要条件是a⊥b；③若函数f(x)为偶函数，则必有f(-x)=f(x)=f(x)恒成立.

　其中正确命题的番号是　　　.

三、解答题：(本大题共6小题，共70分)解答应写出文字说明、证明过程或推演步骤.

17.(共10分)已知函数f(x)=sin(x+)+sin(x-)+cosx+a(a∈R，a为常数).

(Ⅰ)求函数f(x)的最小正周期；

(Ⅱ)若函数f(x)在[-，]上的最小值为－1，求实数a的值.

18.(共10分)

　 一纸箱中放有除颜色外，其余完全相同的黑球和白球，其中黑球2个，白球3个.

(Ⅰ)从中同时摸出两个球，求两球颜色恰好相同的概率；

(Ⅱ)从中摸出一个球，放回后再摸出一个球，求两球颜色恰好不同的概率.

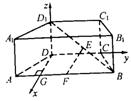
19.(共12分)如图，直四棱柱ABCD-A1B1C1D1中，底面ABCD是等腰梯形，AB∥CD，AB=2AD=2DC=2,E为BD1的中点，F为AB的中点.

　 (Ⅰ)求证：EF∥平面ADD1A1；

　 (Ⅱ)建立空间直角坐标系D-xyz(DG是AB边上的高)，若BB1=，求A1F与平面DEF所成的角的大小.

20.(共12分)已知函数f(t)=log2t,t∈[,8]

　 (Ⅰ)求f(t)的值域G；

　 (Ⅱ)若对于G内的所有实数x，不等式-x2+2mx-m2+2m≤1恒成立，求实数m的取值范围.

21.(共13分)已知等差数列{an}中，a1=1,公差d>0，且a2、a5、a14分别是等比数列{bn}的第二项、第三项、第四项.

　  (Ⅰ)求数列{an}、{bn}的通项an、bn;

　  (Ⅱ)设数列{cn}对任意的n∈N*，有+…＋＝an+1成立，求c1+c2+…+c2005的值.

22．(共13分)设向量=(1,0),=(0,1),=x+(y+2),=x+(y-2),且｜｜＋｜｜＝8，x，y∈R.

　  (Ⅰ)求点P(x,y)的轨迹C的方程；

　  (Ⅱ)已知点M(0,3)作曲线l与曲线C交于A、B两点，设=+，问是否存在直线l，使四边形OANB为矩形？若存在，求出直线l的方程；若不存在，请说明理由.

绝密★启用前

成都市2006届高中毕业班摸底测试

数学试题(文科)参考答案及评分意见

一、选择题：（每小题5分，共60分）

1.D　2.B　3.A　4.A　5.C　6.C　7.B　8.C　9.A　10.D　　　 11.D 12.B

二、填空题：(每小题5分，共20分)

　　13.1024或21D　　14.2　　 15.(-2,-1)　　　16.②③

三、解答题(本大题共6小题，共70分)

17.解：(Ⅰ)∵f(x)-2sinxcos=

　　　　　　　　　　　　　　=2sin(x+　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ……3分

∴函数f(x)的最小正周期T=2π.　　　　　　　　　　　　　　　　　　　　　　　 ……2分

(Ⅱ)∵x∈[－]，∴－≤x+≤.

∴当x+=－,即x=－时， fmin(x)=f(－)=－+a.　　　 ……3分

由题意，有－+a=－1.

∴a=－1.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　……2分

18.解：(Ⅰ)摸出两球颜色恰好相同，即两个黑球或两个白球，共有C+C=4(种)可能情况.　　　故所求概率为P== 　　　　　　　　　　　　　　　　　 　　　　　 ……5分

(Ⅱ)有放回地摸两次，两球颜色不同，即“先黑后白”或“先白后黑”.

故所求概率为P==　　　　　　　　　　　　 ……5分

19.(Ⅰ)证明：连AD1.　　　　　 　 ……1分

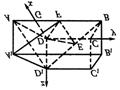在ΔABD1中，∵E、F分别是BD1、AB的中点，

∴EF∥AD1.

又EF平面ADD1A1,

∴EF∥平面ADD1A1.　　　　　　　　　　　　　　　　　　　　 ……5分

(Ⅱ)解：在空间直角坐标系D－xyz中，

有A1(),F(0),D1(0,0,),B().

∴E().　　　　　　　　　　　　　　　　　　　　　　　　……2分

设平面DEF的法向量为=(x,y,z).

由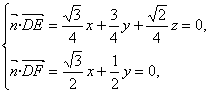

取非零法向量=(1,－).　　　　　　　　　　　　　 ……2分

∵

∴A1F与平面DEF所成的角即是与n所成锐角的余角.

由cos＜,n＞==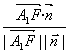

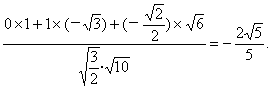
∴A1F与平面DEF所成角的大小为－arccos即arcsin ……2分

　　　 20.解：(Ⅰ)∵f(t)=log2t在t∈[,8]上是单调递增的，∴log2≤log2t≤log28.

即≤f(t)≤3.

∴f(t)的值域G为[].　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ……5分

(Ⅱ)由题知－x2+2mx－m2+2m≤1在x∈[]上恒成立

*－2mx+m2－2m+1≥0在x∈[]上恒成立.

令g(x)=x2－2mx+m2－2m+1,x∈[].

只需gmin(x)≥0即可.

而g(x)=(x－m)2－2m+1,x∈[].

(1)当m≤时，gmin(x)=g()=－3m+m2+1≥0.

∴4m2－12m+5≥0.解得m≥或≤.

∴m≤　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ……2分

(2)当＜m＜3时，gmin(x)=g(m)= －2m+1≥0.

解得m≤

这与＜m＜3矛盾.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　……2分

(3)当m≥3时，gmin(x)=g(3)=10+m2－8m≥0.

解得m≥4+或m≤4－.

而m≥3,∴m≥4＋.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ……2分

综上，实数m的取值范围是 (－∞，]∪[4+，+∞).　　　　 ……1分

　　　 21.解：(Ⅰ)由题意，有 (a1+d)(a1+13d)=(a1+4d)2.　　　　　　　　　　　　　　　 ……2分

而a1=1, d>0，∴d=2.

∴an=2n－1.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　……3分

公比q==3,a2=b2=3.

∴bn=b2·qn－2=3·3n－2= 3n－1.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ……2分

(Ⅱ)当n=1时，,∴c1=1×3=3.

当n≥2时，

∵　　　　　　　　　　　……①

　　　　　　 ……②

②—①，得=an+1－an=2,

∴cn=2bn=2·3n－1(n≥2).

即有cn=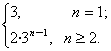　　　　　　　　　　　　　　　　　　　　　　　　　　　 ……4分

∴c1+ c2+ c3+…+ c2005=3+2(31+32+33+…+32004)

=3+2·=32005. 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ……2分

22.解：(Ⅰ)∵=(1，0)，=(0，1), +=8,

∴　　　　　　　　　　　　　　　　　　　　　……2分

上式即为点P(x,y)到点(0，－2)与到点(0，2)距离之和为8.

记F1(0，－2)，F2(0，2)，则F1F2=4.

即PF1+PF2=8＞F1F2.

∴P点轨迹C为以F1、F2为焦点的椭圆.

其中2a=8,2c=4.　　　　∴b2=a2－c2=12.

∴所求轨迹C的方程为　　　　　　　　　　　　　　　　　　　　　……4分

(Ⅱ)∵,∴OANB是平行四边形.

∵l过点M(0，3).

若l是y轴，则A、B是椭圆的顶点.此时.

∴N与O重合，与四边形OANB是平行四边形矛盾.

故直线l的斜率k必存在.

设直线l的方程为y=kx+3.　　　　　　　　　　　　　　　　　　　　　　　　　　　　……1分

设A(x­1,y1),B(x­2,y2).

若存在直线l使得OANB是矩形，则OA⊥OB.

∴

∴x1x2+y1y2=0.

而y1y2=(kx1+3)(kx2+3) =k2x1x2+3k(x1+x2)+9.

∴(1+k2)x1x2+3k(x1+x2)+9=0.　　　　　　　　　　　　　　　　……①　　　　　 ……2分

由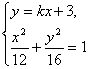

消去y，得(3k2+4)x2+18kx－21=0

∵Δ＝(18k)2－4(3k2+4)(－21)=(18k)2+84(3k2+4)＞0,

∴方程②必有两实数根x1、x2.

且x1+x2=,x1x2=－

代入①，得－(1+k2)·

解得k2=,∴k=±.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ……3分

∴存在直线l符合题意，其直线方程为

y=±即x－y+3=0或　　　　　　　　　　　 ……1分