传承世纪2006届高三年级形成性综合探究试卷（二）
数学（理科）试题
参考公式：
如果事件A、B互斥，那么
球的表面积公式 
P(A+B)=P(A)+P(B)
如果事件A、B相互独立，那么 其中R表示球的半径球的体积公式
P(A·B)=P(A)·P(B)
如果事件A在一次试验中发生的概率是 
P，那么n次独立重复试验中恰好发生k
次的概率
其中R表示球的半径
一、选择题（本大题共12小题，每小题5分，共60分，每小题给出的4个选项中，只有1
项是符合题要求的）
1．设
，则满足
的集合A，B的组数是 （ ）
A．1组 B．2组 C．4组 D．6组
2．若
，则下列各式中成立的是 （ ）
A．
B．
C．
D．
3．在
中，如果
，则角A等于 （ ）
A．
B．
C．或 D．
4．已知数列
的值为 （ ）
A．
B．
C．1 D．－2
5．直线
有交点，但直线不过圆心，则
（ ）
A．
B．
C．
D．
6．如图，在正三角形中，D、E、F分别为各边的中点，G、
H、I、J分别为AF，AD，BE，DE的中点，将沿DE，
EF，DF折成三棱锥以后，GH与IJ所成角的度数为 （ ）
A．90° B．60°
C．45° D．0°
7．已知以
为自变量的目标函数
的可行域
如图阴影部分（含边界），若使
取最大值时的最优解有无穷
多个，则k的值为 （ ）
A．1 B．
C．2 D．4
8．若
，则函数
的最小值是（ ）
A．1 B．－1 C．
D．－2
9．一个正四面体外切于球O1，同时又内接于球O2，则球O1与球O2的体积之比为（ ）
A．
B．
C．
D．
10．若把英语单词“hello”的字母顺序写错了，则可能出现的错误的种数是 （ ）
A．119 B．59 C．120 D．60
11．E，F是随圆
的左、右焦点，l是椭圆的一条准线，点P在l上，则∠EPF
的最大值是 （ ）
A．15° B．30° C．60° D．45°
12．关于甲、乙、丙三人参加高考的结果有下列三个正确的判断：①若甲未被录取，则乙、
丙都被录取；②乙与丙中必有一个未被录取；③或者甲未被录取，或者乙被录取，则三
人中被录取的是 （ ）
A．甲 B．丙 C．甲与丙 D．甲与乙
二、填空题（本大题共4个小题，每小题4分，共16分，把答案填在题中的横线上.）
13．把函数
的图象按向量a平移后，得
的图象，则a= .
14．已知关于x的不等式
的解集为M，若
，则实数a的取值范
围是 .
15．设
的反函数的解析式是
.
16．若E，F分别是四棱柱ABCD—A1B1C1D1的棱AB，AD
的中点，则加上条件 ，
就可得结论：EF⊥平面DA1C1. （写出你认为正确的一个
条件即可）
三、解答题（本大题共6小题，共74分，解答时应写出文字说明、证明过程或演算步骤.）
17．（本小题满分12分）A，B两工人在同样条件下每天生产的产品件数相同，而两人出次
品个数的分布列分别为
（A） （B）
 |
根据优胜劣汰、竞争上岗的原则，A，B中的一个已经待岗了，你认为是哪一个？为什
么？
18．（本小题满分12分）
（1）已知：
；
（2）已知：
的值.
19．（本小题满分12分）如图，已知四棱锥P——ABCD中，底面ABCD为正方形，侧面PDC
为正三角形，且平面PDC⊥底面ABCD，E为PC的中点.
（1）求证：PA//平面EDB；
（2）求证：平面EDB⊥平面PBC；
（3）求二面角D—PB—C的大小.
20．（本小题满分12分）已知函数
在区间[0，1]上单调递增，在
区间[1，2]上单调递减.
（1）求a的值；
（2）设
，若方程
的解集恰有3个元素，求b的取值范围；
（3）在（2）的条件下，是否存在实数对（m，n），使
为偶函数？
如存在，求出m，n；如不存在，说明理由.
21．（本小题满分12分）有人玩掷硬币走跳跳棋的游戏，已知硬币出现正反面的概率都是
棋盘上标有第0站、第1站、第2站、…第100站. 一枚棋子开始在第0站，棋手每掷
一次硬币，棋子向前跳动一次. 若掷出正面，棋向前跳一站（从k到k+1）；若掷出反面，
棋子向前跳二站（从k到k+2），直到棋子跳到第99站（胜利大本营）或跳到第100站
（失败集中营）时，该游戏结束. 设棋子跳到第n站的概率为Pn.
（1）求P0，P1，P2的值；
（2）求证：
；
（3）求P99及P100的值.
22．（本小题满分14分）如图所示，点
点P在
轴上运动，M在x轴上，N
为动点，且
0
（1）过点N的轨迹C的方程；
（2）过点
的直线l（不与x轴垂直）与曲线C交于A，B两点，设点
，
的夹角为
，求证：
数学（理科）参考答案
1.D 2.C 3.A 4.C 5.B 6.B 7.A 8.A 9.D 10.B 11.B 12.D
13．（－1，－3） 14．
15．
16．底面是菱形且DC1⊥底面（或填AB=BC，AD=CD，DA⊥底面；或填底面是正方形，
DA1⊥A1B1，DA1⊥A1D1等等）
17．
两人出次品的期望相同.又
又
说明A的波动大，B的技术稳定性强，水平较高. 不出意外，应当是A待岗了.
18．（1）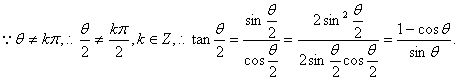
（2）
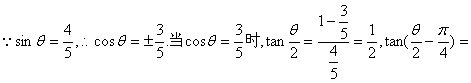
当
19．（1）连AC交BD于O，连EO，由四边形ABCD为正方形，
得O为AC中点，在△PAC中，由中位线定理得EO//PA 又
EO
平面EDB，PA
平面EDB，∴PA//平面EDB.
（2）由平面PDC⊥平面ABCD，BC⊥DC，得BC⊥平面PDC.
又DE平面PDC，则BC⊥DE. E为PC的中点，△PDC为正
三角形，∴DE⊥PC. BC∩PC=C，∴DE⊥平面PBC. 又DE
平面EDB，∴平面EDB⊥平面PBC.
（3）作EF⊥PB于F，连DF，由DE⊥平面PBC及三垂线定理
得DF⊥PB.∠DFE是所求二面角的平面角. 设BC=4，则PC=4. 在等边△PDC中求出
DE=
. 在Rt△PFE中，∠EPF=45°，PE=2，可求出FE=
，
∴二面角D—PB—C的大小为
20．（1）
，由已知
上的值恒为正，在
上的值恒
为负，故x=1是
（2）由
有三个相异实根，故方程
有两个相异的非零根. 
（3）
为偶函数.
21．（1）棋子开始在第0站为必然事件，
，第一次掷硬币出现正面，棋子跳到第1
站，其概率为
，棋子跳到第二站应从如下两方面考虑：①第二次掷硬币都
出现正面，其概率为
；②第一次掷硬币出现反面，其概率为
（2）棋子跳到第
站的情况是下列两种，而且也只有两种：①棋子先到第
n－2站，又掷出反面，其概率为
；②棋子先到第n－1站，又掷出正面，其概率
为
（3）由（2）知，当
时，数列
是首项为
，公比为
的等比数列.
以上各式相加，得
22．（1）设
则
由
①
0，
0，即
并代入①，
得
为所求.
（2）设l的方程为
设
则
