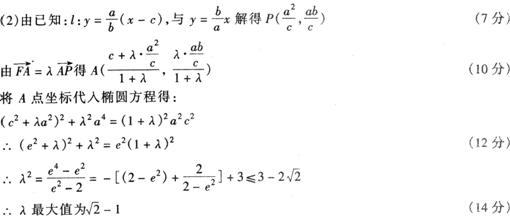传承世纪2006届高三年级形成性综合探究试卷（一）
数学试题(文科)
一、选择题(每小题5分，共60分)
1.如果向量 =(k，1)，与
= (4，k)共线且方向相反，则k =
A．±2 B．-2 C．2 D．0
2．函数f(x)=( )x(1<x≤2)的反函数f-1(x)等于
A.log x(1<x≤2)
B.
log x(2<x≤4)
C.-log2x(
≤x＜ ﹞
D. -log2x( ≤x＜1〕
3.已知P=｛x︱x≤0｝,Q=｛x︱x＜ ｝,则Q∩CRP等于
|
A.｛x︱x≤0｝ B.｛x︱0≤x＜ }
C. {x0<x< }
D. {xx>0}
4．已知α、β都是第二象限角，且cos >cosβ，则
A ． <β B．sin >sinβ C．tan >tanβ D．cot <cotβ
5．已知奇函数f(x)的定义域为：{x｜x+2-a｜＜a，a>0}，则a的值为
A．1 B．2 C．3 D．4
6．方程Ax+By+C=0表示倾斜角为锐角的直线，则必有：
A. A﹒B>0 B．A﹒B<0 C．A>0且B<0 D．A>0或B<0
7．已知f(x)=ax(a>0且a≠1),f-1(2)<0，则f-1(x+1)的图象是
8．如果方程
表示双曲线，则下列椭圆中，与该双曲线共焦点的是
A. B.
C.
D.
9．把正整数按下图所示的规律排序，则从2003到2005的箭头方向依次为
10.已知函数f(x)=2sin(ωx+ )图象与直线y=1的交点中，距离最近两点间的距离为 ，那
么此函数的周期是
A .
B．
C．2π
D．4π
| |
11．点p到点A( ，0)，B(a，2)及到直线x=- 的距离都相等，如果这样的点恰好只有一
个，那么a的值是
|  | | | | |
A. B. C. 或 D.- 或
 |
12.设 P(x,y)是曲线 上的点，F1(-4,0),F2(4,0),则
A.｜F1P︳+ ︱F2P︳<10 B．｜F1P｜+｜F2P｜>10
C.｜F1P︳+｜F2P︳≤10 D．｜F1P｜+｜F2P｜≥10
二、填空题与连线题(每小题4分，共16分)
13．若函数 y=2x2+4x+3的图象按向量 平移后，得到函数y=2x2的图象，则： =
.
14．已知(x，y)在映射f下的象是(x+Y，-x)，则(1，2)在f下原象是 .
15．圆x2+y2+x-6y+3=0上两点P、Q关于直线kx-y+4=0对称，则k= .
16.在△ABC中，B（-2，0），C（2，0），A（x,y）,给出△ABC满足的条件，就能得到动点A的轨迹方程，下面给出了一些条件及方程，请你用线把左边满足的条件及相应的右边A点的轨迹方程连起来：（错一条连线得0分）
三、解答题
17．（12分）已知sin -cos = ,a∈( ,
),tan( - )=
.求tan( )的值。
18．(12分)解关于x的不等式｜ x-a ｜<ax (a>0)．
19．(12分)如图，在平面斜坐标系xOy中，∠xOy=600，平面上任一点P关于斜坐标系的斜坐
标是这样定义的：
若 =x +y ，(其中 、 分别为与x轴，y轴同方向的单位向量)，则P点斜坐标为
(x，y)．
(1)若P点斜坐标为(2，-2)，求P到0的距离｜ PO ｜；
(2)求以0为圆心，1为半径的圆在斜坐标系xOy中的方程．
20．(12分)已知有三个居民小区A、B、C构成三角形ABC，这三个小区分别相距BC=800m、
AB=700m、Ac=300m．为解决居民就业，服务小区生活，在与A、B、C三个小区距离相等处
建造一个食品加工厂．同时为了不影响小区居民的正常生活和休息，在厂房的四周需要安
装隔音窗或建造隔音围墙。根据以往经验．机器从厂房发出的噪音是85分贝，而维持居民
正常生活和休息时的噪音不得超过50分贝，每安装一道隔音窗噪音降低3分贝，花费3万
元。隔音窗不能超过3道；每建造一堵隔音墙噪音降低15分贝．花费10万元；距离厂房平
均每25m噪音均匀降低1分贝．
(1)求加工厂距A区的距离．( ≈1.732，精确到1 m)；
(2)怎样建造隔音设备，使其隔音设备成本最低?
21．（ 12分）已知等比数列{an}的公比为q，前n项的和为Sn，且S3，S9，S6成等差数列．
(1)求q3的值；
(2)求证：a2，a8，a5成等差数列．
22．(14分)已知椭圆C的方程为
(a>b>0)，双曲线
的两条渐近线为l1、
l2,过椭圆C的右焦点F作直线l，使l⊥l1，，又l与l2交于P点，设l与椭圆C的两个交点
由上至下依次为A、B．(如图)
(1)当l1与l2夹角为600，双曲线的焦距为4时，求椭圆C的方程．
(2)当
时，求λ的最大值．
数学参考答案
1．B 2．C 3．C 4．B 5．B 6．B 7．A 8．D 9．B 10．B 11．D 12．C
7．f -1(2)<0得f -1(2)=loga2<0,∴0<a<1，向左平移一个面位即得A．
8．由题意有pq>0，若P>0，q>O，则双曲线焦点位于Y轴上且C2=P+q无答案，则只有P<0，q<0，焦点位于x轴上，且C2=-P-q，D答案符合．
二、13．(1，-1)
14．(-2，3) 15．2 16.
(①→c ②→a ③→b)
三、
 |
(2分)
(4分)
(6分)
(8分)
(10分)
(12分)
18．原不等式等价于：-ax<x-a<ax (2分)
20．(1)由题设知，所求距离为△ABC外接圆半径R
(2)设需要安装x道隔音窗，建造Y堵隔音墙，总成本为S万元，由题意得：
其中S=3x+lOy (9分)
∴当x=2，y=l时，S最小值为16万元 (11分)
故安装两道隔音窗，建造一堵隔音墙 (12分)
21．(1)由S3、S9、S6成等差数列，得S3+S6=2S9 (2分)
若q=1，则S3+S6=9a1又2S9=18a1
由a1≠0，得S3+S6≠2S9 ∴q≠1 (4分)
由S3+S6=2S9得q3+q6=2q9
