柳州实验高中2005-2006上期高三年级二次月考数学试卷(理科卷)
说明:1、本套试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,共6页.考试时间为120分钟.
2、本卷考试内容:概率、极限、导数、复数、集合与简易逻辑
第Ⅰ卷(选择题,共60分)
一、选择题:(每小题5分,共60分.每小题只有一项是符合题目要求的.请把答案写在答案卷上。)
1.设U = R ,集合![]() ,
,![]() ,则
,则![]() 是(
)
是(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.![]() = ( )
= ( )
A.![]() B.1
C.
B.1
C.![]() D.
D.![]()
3.已知p:![]() q:
q:![]() 则p是q的( )
则p是q的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4.与直线![]() 平行的曲线
平行的曲线![]() 的切线方程是 ( )
的切线方程是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 或
或![]()
5.设随机变量![]() 的分布列为
的分布列为![]() 则
则![]() 的值是( )
的值是( )
A.1
B.![]() C.
C.![]() D.
D.![]()
6.已知函数y=f(x)在区间(a,b)内可导,且x 0∈(a,b)则![]() 的
的
值为( ) A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.已知不等式![]() 对
对![]() 恒成立,则a的取值范围是( )
恒成立,则a的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.若对![]() ,不等式
,不等式![]() 恒成立,则k的范围是( )
恒成立,则k的范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.复数![]() = ( )
= ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10、用数学归纳法证明![]() 时,第一步即证下述哪个不等式成立( )
时,第一步即证下述哪个不等式成立( )
 A.1<2
B.
A.1<2
B.![]() C.
C.![]() D.
D.![]()
11.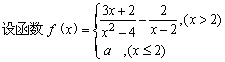 在x=2处连续,则a = ( )
在x=2处连续,则a = ( )
A.![]() B.
B. ![]() C .
C .![]() D.
D. ![]()
12.已知函数![]()
![]() ,下面四个图象中
,下面四个图象中![]() 的图象大致是( )
的图象大致是( )
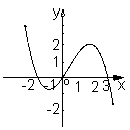
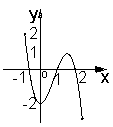
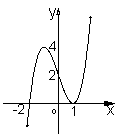
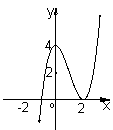
A B C D
第Ⅱ卷 (非选择题,共90分)
二、填空题:(每小题4分,共16分. 把答案写在答题卷上.)
13.![]() =
=
14. 若函数 ![]() = x·2x 且
= x·2x 且![]() =0 ,则x =
=0 ,则x =
15.设![]() ,若
,若![]() ,
,![]() ,则n,P的值分别是
,则n,P的值分别是
16.某保险公司新开设了一项保险业务,若事件E发生,则该公司要赔偿![]() 元,设在一年内E发生的概率为p,为使公司受益的期望值等于
元,设在一年内E发生的概率为p,为使公司受益的期望值等于![]() 的,公司应要求顾客缴纳的保险金为
的,公司应要求顾客缴纳的保险金为
柳州实验高中2005-2006上期高三年级第一次月考数学答卷(理科卷)
第Ⅰ卷
|
| 一 | 二 | 三 | 总分 | ||||||
| 17 | 18 | 19 | 20 | 21 | 22 | |||||
| 得分 | ||||||||||
一、选择题(每题5分,共60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | A | A | D | D | B | B | B | A | C | C | C |
第Ⅱ卷 (非选择题,共90分)
二、填空题(每题4分,共16分)
13、 -3
14、 ![]()
15、 ![]() 16、 ap+
16、 ap+ ![]()
三、解答题(共74分)
17. (12分)解关于x 的不等式:![]() (x∈R)
(x∈R)
解:原不等式可化为:![]() ………………………………2分
………………………………2分
(1)当a =0时,原不等式可化为![]()
当a =1时,原不等式可化为![]() ……………4分
……………4分
(2)当a <0或a>1时,![]() 原不等式 的解集为
原不等式 的解集为![]() ……8分
……8分
(3)当0<a <1时,![]() 原不等式的解集为
原不等式的解集为![]() …………12分
…………12分
综上所述:当a =0或a =1时,原不等式的解集为![]() ;
;
当0<a <1时,![]() 原不等式的解集为
原不等式的解集为![]()
当a <0或a>1时,![]() 原不等式 的解集为
原不等式 的解集为![]()
(不写结论扣1分)
18.(12分).已知命题p:x2 + mx + 1 = 0有两个不等的负根,命题q:4x2 + 4(m – 2 )x + 1 = 0无实根,若命题p与命题q有且只有一个为真,求实数m的取值范围.
解:∵x2 + mx + 1 = 0有两个不等的负根,
∴![]() ,得m
> 2…………………….4分
,得m
> 2…………………….4分
∵4x2 + 4(m – 2 )x + 1 = 0无实根,
∴ 16(m – 2 )2 – 16 < 0 , 得 1 < m < 3 ……………….4分
有且只有一个为真,
若p真q假,得 m ³ 3
若p假q真,得 1 < m £ 2.
综合上述得m ³3,或1< m £ 2 . …………………..12分
19.(12分)已知函数![]() 的图象与y轴的交点为P,且曲线在P点处的切线方程为24x + y –12 = 0,若函数在 x = 2 处取得极值 –16.
的图象与y轴的交点为P,且曲线在P点处的切线方程为24x + y –12 = 0,若函数在 x = 2 处取得极值 –16.
(1) 求f (x)的解析式;
(2) 确定f (x)的单调递减区间。
.解:(1)切线方程为:![]() 与y轴的交点为p(0,12)代入
与y轴的交点为p(0,12)代入![]() 得d=12………….………………..2分
得d=12………….………………..2分
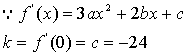 …………………………………..…..4分
…………………………………..…..4分
![]() …………………………..…..5分
…………………………..…..5分
又因函数f(x)在x=2处的极值为-16
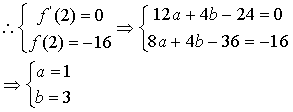 ………………..…..9分
………………..…..9分
![]()
(2)由(1)知:![]() 令
令![]() …..…11分
…..…11分
所以原函数的单调递减区间为(-4,2)……………….12分

 20.(12分)如图所示,铁路线上AB段长100km,工厂C到铁路的距离CA=20km,现在要在AB上某处D向C修建一条公路,已知铁路每吨公里与公路每吨公里的运费之比为
20.(12分)如图所示,铁路线上AB段长100km,工厂C到铁路的距离CA=20km,现在要在AB上某处D向C修建一条公路,已知铁路每吨公里与公路每吨公里的运费之比为
3∶5,为了使原料从B处运到C处的运费最省,D应修在何处?
 C
C
B D A
解:设DA = x km,则DB = (100
– x )km CD = ![]() km………2分
km………2分
又设铁路上每吨公里运费为3t元,则公路上每吨公里运费为5t元,这样每吨原料从B到C的总运费为y
= 5t·CD + 3t·BD = 5t![]() +3t(100 – x ), x∈[0,100]…….6分
+3t(100 – x ), x∈[0,100]…….6分
∴y′ = t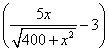 ,
令y′ = 0得,解得 x = 15 km, ……………….10分
,
令y′ = 0得,解得 x = 15 km, ……………….10分
在x = 15 附近,y′ 是左负右正,所以y = 15 取得极小值,即为最小值。
∴D应选在距A为15km处。………………….12分
21.(14分) 如图,A、B两点之间有6条网线并联,它们能通过的最大信息量分别为1,1,2,2,3,4。现从中任取三条网线且使每条网线通过最大信息量。
(1)
设选取的三条网线由A到B可通过的信息总量为x,当![]() 时,则保证信息畅通,
时,则保证信息畅通,
求线路信息畅通的概率;
(2)
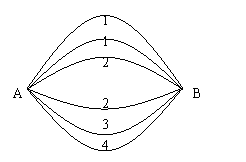 求选取的三条网线可通过信息总量的数学期望。
求选取的三条网线可通过信息总量的数学期望。
解 :
|
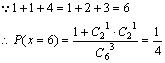
|
|
|
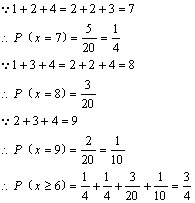
|
|

22.(12分)设![]() 是由正数组成的数列,其前n项和为
是由正数组成的数列,其前n项和为![]() ,
,
且满足关系:![]()
(1)求数列![]() 的通项公式(写出推导过程);
的通项公式(写出推导过程);
(2)若![]() ,求
,求![]()
解:(1)当![]() 时,
时,![]() ,解得
,解得![]() 。
。
当![]() 时,
时,![]() ,解得
,解得![]() 。
。
当![]() 时,
时,![]() ,解得
,解得![]() 。
。
猜想![]() ……4分
……4分
证明:当![]() 时,
时,![]() 成立。
成立。
假设当![]() 时,
时,![]()
![]()
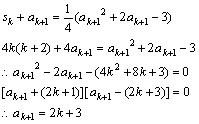
![]() 当
当![]() 时,猜想成立,
时,猜想成立,
![]() 当
当![]() 为任意正整数时,都有
为任意正整数时,都有![]() 。
…… 8分
。
…… 8分
|
|
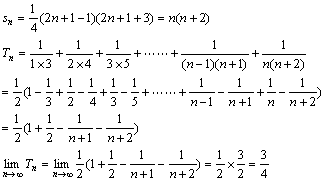

 题号
题号