2006年杭州市第二次高考科目教学质量检测
数学试题卷(文科)
考生须知:
1. 本卷满分150分, 考试时间120分钟.
2. 答题前, 在答题卷密封区内填写学校、班级和姓名.
3. 所有答案必须写在答题卷上, 写在试题卷上无效.
4. 考试结束, 只需上交答题卷.
参考公式
如果事件![]() 互斥,那么
互斥,那么![]() ;
;
如果事件![]() 相互独立,那么
相互独立,那么![]() ;
;
如果事件![]() 在一次试验中发生的概率是
在一次试验中发生的概率是![]() ,那么
,那么![]() 次独立重复试验中恰好发生
次独立重复试验中恰好发生![]() 次的概率
次的概率![]() .
.
一. 选择题 : 本大题共10小题, 每小题5分, 共50分. 在每小题给出的四个选项中, 只有一项是符合题目要求的 .
1. 若集合![]() , 则满足
, 则满足![]() 的集合
的集合![]() 的个数是
的个数是
(A) 6 (B) 7 (C) 8 (D) 10
2. 函数![]() R 是
R 是
(A) 最小正周期为![]() 的偶函数 (B) 最小正周期为
的偶函数 (B) 最小正周期为![]() 的奇函数
的奇函数
(C) 最小正周期为![]()
![]() 的偶函数 (D) 最小正周期为
的偶函数 (D) 最小正周期为![]()
![]() 的奇函数
的奇函数
3. 椭圆![]() 的准线与
的准线与![]() 轴平行, 那么
轴平行, 那么![]() 的取值范围为
的取值范围为
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
4. 已知 a = b = 2, a·b = -2, 且(a +
b)⊥(a +
![]() b), 则实数
b), 则实数![]() 的值为
的值为
(A) –1 (B) 1 (C) –2 (D) 2
5. 光线沿直线![]() 射到直线
射到直线![]() 上, 被
上, 被![]() 反射后的光线所在的直线方程为
反射后的光线所在的直线方程为
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
6. 若![]() 是两个相交平面, 点
是两个相交平面, 点![]() 不在
不在![]() 内, 也不在
内, 也不在![]() 内, 则过点
内, 则过点![]() 且与
且与![]() 和
和![]() 都平行的直线
都平行的直线
(A) 只有1条 (B) 只有2条 (C) 只有4条 (D) 有无数条
7. 停车场可把12辆车停放在一排上, 当有8辆车已停放后, 而恰有4个空位在一起, 这样的事件发生的概率是
(A) ![]() (B)
(B)
![]() (C)
(C)
![]() (D)
(D)
![]()
8. 对于二项式![]()
![]() , 有四个判断: ① 存在
, 有四个判断: ① 存在![]() , 展开式中有常数项; ② 对任意
, 展开式中有常数项; ② 对任意![]() , 展开式中没有常数项; ③ 对任意
, 展开式中没有常数项; ③ 对任意![]() , 展开式中没有
, 展开式中没有![]() 的一次项; ④ 存在
的一次项; ④ 存在![]() , 展开式中有
, 展开式中有![]() 的一次项. 上述判断中正确的是
的一次项. 上述判断中正确的是
(A) ①与③ (B) ②与③ (C) ②与④ (D) ①与④
|
(第9题) |
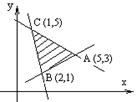
9. 给出平面区域![]() , 如图所示, 其中
, 如图所示, 其中![]()
![]() . 若使目标函数
. 若使目标函数![]() 取得最大值
取得最大值
的最优解有无穷多个, 则![]() 的值为
的值为
(A) 4 (B) 2 (C) ![]() (D)
(D) ![]()
10. 已知函数![]() , 函数
, 函数![]() 定义如下: 当
定义如下: 当![]() 时,
时, ![]() ; 当
; 当![]() 时,
时, ![]() .
.
那么![]()
(A) 有最小值0, 无最大值 (B) 有最小值-1, 无最大值
(C) 有最大值1, 无最小值 (D) 无最小值, 也无最大值
二.填空题: 本大题有4小题, 每小题4分, 共16分. 把答案填在答题卷的相应位置.
11. 请举出一个反例: ______, 说明命题“奇函数必存在反函数”是假命题.
12. 圆心在直线![]() 上, 且过点
上, 且过点![]() 的圆的方程是 _______ .
的圆的方程是 _______ .
|
(第13题) |
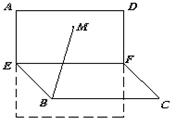
13. 正方形![]() 的边长是2,
的边长是2, ![]() 分别是
分别是![]()
和![]() 的中点, 将正方形沿
的中点, 将正方形沿![]() 折成直二面角(如
折成直二面角(如
图所示). ![]() 为矩形
为矩形![]() 内一点, 如果
内一点, 如果![]()
![]() 和平面
和平面![]() 所成角的正切值为
所成角的正切值为![]() ,
,
那么点![]() 到直线
到直线![]() 的距离为 _______ .
的距离为 _______ .
14. 某健康中心研究认为:身高为![]() (cm)的人的其理想体重
(cm)的人的其理想体重![]() (kg),应符合公式
(kg),应符合公式![]() =22
=22![]() 2
(kg),且定义体重在理想体重±10%的范围内,称为标准体重;超过10%但不超过20%者,称为微胖;超过20%者,称为肥胖, 微胖及肥胖都是过重的现象. 对身高
2
(kg),且定义体重在理想体重±10%的范围内,称为标准体重;超过10%但不超过20%者,称为微胖;超过20%者,称为肥胖, 微胖及肥胖都是过重的现象. 对身高![]() ,体重
,体重![]() 的人,体重过重的充要条件为
的人,体重过重的充要条件为![]() ,则
,则![]() __________ .
__________ .
三. 解答题: 本大题有6小题, 每小题14分,共84分. 解答应写出文字说明, 证明过程或演算步骤.
15. (本小题满分14分)
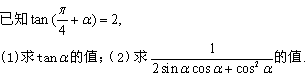
16. (本小题满分14分)
已知数列{![]() }是首项为
}是首项为![]() 等于1且公比
等于1且公比![]() 不等于1的等比数列,
不等于1的等比数列,![]() 是其前
是其前![]() 项的和,
项的和,![]() 成等差数列.
成等差数列.
(1) 求和 ![]() ;
;
(2) 证明 12![]() 成等比数列.
成等比数列.
17.(本小题满分14分)
设甲、已、丙三人每次射击命中目标的概率分别为0.7、0.6和0.5.
(1) 三人各向目标射击一次,求至少有一人命中目标的概率;
(2) 三人各向目标射击一次,求恰有两人命中目标的概率;
(3)若甲单独向目标射击三次,求他恰好命中两次的概率.
18 . (本小题满分14分)
|
(第18题) |
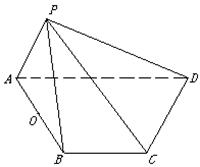
如图, 在四棱锥![]() 中,顶点
中,顶点![]() 在底面
在底面![]() 上的射影恰好落在
上的射影恰好落在![]() 的中点
的中点![]() 上,又∠
上,又∠![]() ,
,![]() ,且
,且![]()
=1:2:2.
(1) 求证: ![]()
(2) 若![]() , 求直线
, 求直线![]() 与
与![]() 所成的角的余弦值;
所成的角的余弦值;
(3) 若平面![]() 与平面
与平面![]() 所成的角为
所成的角为![]() , 求
, 求![]() 的值.
的值.
19. (本小题满分14分)
已知奇函数![]() 有最大值
有最大值![]() , 且
, 且![]() , 其中实数
, 其中实数![]() 是正整数.
是正整数.
(1)
求![]() 的解析式;
的解析式;
(2)
令![]() , 证明
, 证明![]() (
(![]() 是正整数).
是正整数).
20. (本小题满分14分)
|
(第20题) |
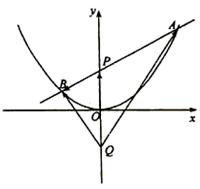
如图,过抛物线![]() 的对称轴上任一点
的对称轴上任一点![]() 作直线与抛物线交于
作直线与抛物线交于![]() 两点,点
两点,点![]() 是点
是点![]() 关于原点的对称点.
关于原点的对称点.
(1) 设点![]() 分有向线段
分有向线段![]() 所成的比为
所成的比为![]() ,证明:
,证明:![]()
![]() ;
;
(2) 设直线![]() 的方程是
的方程是![]() ,过
,过![]() 两点的圆
两点的圆![]() 与抛物线在点
与抛物线在点![]() 处有共同的切线,求圆
处有共同的切线,求圆![]() 的方程.
的方程.
2006年杭州市第二次高考科目教学质量检测
数学参考评分标准(文科)
一. 选择题 : (本大题共10小题, 每小题5分, 共50分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | C | C | D | A | B | A | C | D | A | B |
二.填空题: (本大题有4小题, 每小题4分, 共16分)
11. 如![]() 或
或![]() R)等. 12.
R)等. 12. ![]() .
.
13. ![]() .
14. (24.2,0,0 )
.
14. (24.2,0,0 )
三. 解答题: (本大题有6小题, 每小题14分,共84分)
15. (本小题满分14分)
(1) 由![]() --- 5分
--- 5分
(2) 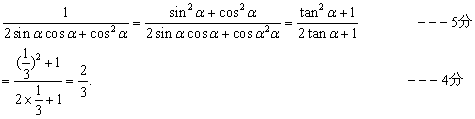
16. (本小题满分14分)
由![]() 成等差数列, 得
成等差数列, 得![]() ,即
,即 ![]() --- 2分
--- 2分
变形得 ![]() 所以
所以![]() (舍去). --- 4分
(舍去). --- 4分
(1) ![]()
![]() ;
;
--- 4分
(2) 由
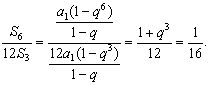
 ,
,
所以12![]() 成等比数列.
--- 4分
成等比数列.
--- 4分
17.(本小题满分14分)
设![]() 表示“第
表示“第![]() 人命中目标”,
人命中目标”,![]() =1,2,3.
=1,2,3.
这里,![]() 相互独立,且
相互独立,且![]() =0.7,
=0.7,![]() =0.6,
=0.6,![]() =0.5. --- 2分
=0.5. --- 2分
(1) 至少有一人命中目标的概率为
![]() ; ---
4分
; ---
4分
(2) 恰有两人命中目标的概率为
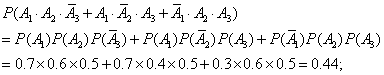 --- 4分
--- 4分
(3) 所求概率为![]() --- 4分
--- 4分
|
|
18 . (本小题满分14分)
因为![]() 中点
中点![]() 为点
为点![]() 在平面ABCD内的射影, 所以
在平面ABCD内的射影, 所以![]() 底面
底面![]() . 以
. 以![]() 为坐标原点,
为坐标原点, ![]() 所在直线为
所在直线为![]() 轴,
轴, ![]() 所在直线为
所在直线为![]() 轴, 建立空间直角坐标系
轴, 建立空间直角坐标系![]() (如图).
(如图).
(1)设![]() , OP = h则依题意得:
, OP = h则依题意得:
![]()
| --- 4分 |
![]() .
.
∴![]() =
= ![]() ,
, ![]() =
= ![]() ,
,
于是![]() ·
·![]() =
= ![]() , ∴
, ∴![]()
(2)由![]() , 得h = a, 于是
, 得h = a, 于是![]() ,
,
| --- 5分 |
∵![]() =
= ![]() ,
, ![]() =
= ![]() , ∴
, ∴![]() ·
·![]() =
= ![]() ,
,
cos<![]() ,
,![]() > =
> = ![]() =
=![]() , ∴ 直线
, ∴ 直线![]() 与
与![]() 所成的角的余弦值为
所成的角的余弦值为![]() ;
;
(3)
设平面![]() 的法向量为m, 可得m = (0,1,0 ),
的法向量为m, 可得m = (0,1,0 ),
设平面![]() 的法向量为n =
的法向量为n = ![]() , 由
, 由![]() =
= ![]() ,
, ![]() =
= ![]() ,
,
∴![]() , 解得n = (1, 2 ,
, 解得n = (1, 2 ,![]() ), ∴ m•n = 2 ,
), ∴ m•n = 2 ,
cos< m, n > = 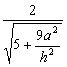 , ∵ 二面角为
, ∵ 二面角为![]() , ∴
, ∴![]() = 4,
= 4,
解得![]() =
=![]() ,即
,即![]() =
=![]() .
--- 5分
.
--- 5分
(以传统方法解答相应给分)
19.(本小题满分14分)
(1) 由奇函数![]() 可得
可得![]() ,
--- 2分
,
--- 2分
x > 0时,由![]() ① 以及
① 以及![]() ②
--- 4分
②
--- 4分
可得到![]() ,
, ![]() , 只有
, 只有![]() , ∴
, ∴![]() ; --- 2分
; --- 2分
(2) ![]() ,
--- 2分
,
--- 2分
则由![]() (
(![]() 是正整数),
是正整数),
可得所求证结论. --- 4分
20. (本小题满分14分)
(1) 依题意,可设直线![]() 的方程为
的方程为 ![]() 代入抛物线方程
代入抛物线方程![]() 得
得
![]() ①
①
设![]() 两点的坐标分别是
两点的坐标分别是 ![]() 、
、![]() 、
、![]() 是方程①的两根.
是方程①的两根.
所以 ![]() ---
2分
---
2分
由点![]() 分有向线段
分有向线段![]() 所成的比为
所成的比为![]() ,得
,得![]()
又点![]() 与点
与点![]() 关于原点对称,故点
关于原点对称,故点![]() 的坐标是
的坐标是![]() ,从而
,从而![]() .--- 2分
.--- 2分
![]() --- 2分
--- 2分
![]()
![]()
![]() 所以
所以
![]() ---
2分
---
2分
(2) 由 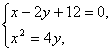 得点
得点![]() 的坐标分别是(6,9)、(-4,4), --- 2分
的坐标分别是(6,9)、(-4,4), --- 2分
由 ![]() 得
得 ![]()
所以抛物线 ![]() 在点
在点![]() 处切线的斜率为
处切线的斜率为![]() ,
--- 2分
,
--- 2分
设圆![]() 的圆心为
的圆心为![]() , 方程是
, 方程是![]()
则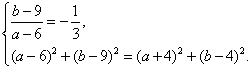 解得
解得 ![]()
则圆![]() 的方程是
的方程是 ![]() (或
(或![]() )
)
--- 2分