南昌十六中2005-2006年高三周练卷(11)
2005-12-08
一、 选择题:(本题每小题5分,共60分)
1、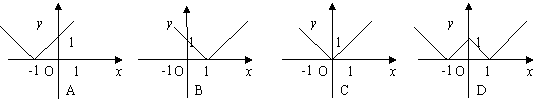
![]() ( )
( )
2、设函数f(x) (x∈R)是以3为周期的奇函数, 且f(1)>1, f(2)= a, 则 A. a>2 B. a<-2 C. a>1 D. a<-1
3、若函数![]() 的反函数的图象过
的反函数的图象过![]() 点,则
点,则![]() 点坐标可能是 ( )
点坐标可能是 ( )
A、(2,5) B、(1,3) C、(5,2) D、(3,1)
4、设f(x)为奇函数, 且在(-∞, 0)内是减函数, f(-2)= 0, 则x f(x)<0的解集为
A. (-1, 0)∪(2, +∞) B. (-∞, -2)∪(0, 2 )
C. (-∞, -2)∪(2, +∞) D. (-2, 0)∪(0, 2 )
5、函数![]() 的反函数的定义域为
的反函数的定义域为
A.![]() B.
B.![]() C.(0,1)
D.
C.(0,1)
D. ![]()
6、下列各图象表示的函数中,存在反函数的只能是 ( )
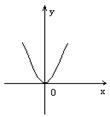
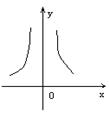
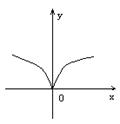
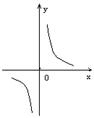
A. B. C. D.
7、设函数f(x)=![]() , 当x∈[-4, 0]时, 恒有f(x)≤g(x), 则a可能取的一个值是
, 当x∈[-4, 0]时, 恒有f(x)≤g(x), 则a可能取的一个值是
A. -5
B. 5
C. -![]() D.
D. ![]()
8、如果函数![]() 是偶函数,那么函数
是偶函数,那么函数![]() 的图象的一条对称轴是直线
的图象的一条对称轴是直线
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9、已知 函数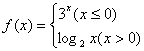 ,那么
,那么![]() 的值为
A. 9
B.
的值为
A. 9
B.![]() C.
C.![]() D.
D.![]()
10、 已知f(x)=ax2+bx+c (a>0),α,β为方程f(x)=x的两根,且0<α<β,当0<x<α时,给出下列不等式,成立的是 ( )
A.x<f(x) B.x≤f(x) C.x>f(x) D.x≥f(x)
11、函数y=logax在![]() 上总有y>1,则a的取值范围是( )
上总有y>1,则a的取值范围是( )
A.![]() 或
或![]() B.
B.![]() 或
或![]()
C. ![]() D.
D.![]() 或
或![]()
12、若方程![]() 有解,则a的取值范围是( )
有解,则a的取值范围是( )
A.a>0或a≤-8 B.a>0
C.![]() D.
D.![]()
二、填空题:(本大题每小题4分,共16分)
13、奇函数![]() 定义域是
定义域是![]() ,则
,则![]() .
.
14、
若![]() ,则
,则![]() ____
____
15、已知函数![]() 的值域是[0,+∞),则实数m的取值范围是__________________。
的值域是[0,+∞),则实数m的取值范围是__________________。
16 、![]() 在R上为减函数,则
在R上为减函数,则![]() .
.
三、解答题:(本大题共6小题,共74分)
17、设![]() 是奇函数,
是奇函数,![]() 是偶函数,并且
是偶函数,并且![]() ,求
,求![]()
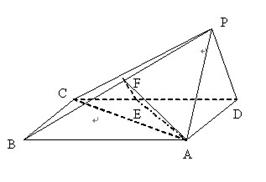
18、四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,AD=PD,E、F分别为CD、PB的中点. (Ⅰ)求证:EF⊥平面PAB
(Ⅱ)设![]() ,求AC与平面AEF所成的角的大小.
,求AC与平面AEF所成的角的大小.
19、已知函数![]()
(1) 当a=-1时,求函数![]() 的最大值和最小值。
的最大值和最小值。
(2)求实数a的取值范围,使得![]()
20、 设A、B是函数y= log2x图象上两点, 其横坐标分别为a和a+4, 直线l: x=a+2与函数y= log2x图象交于点C, 与直线AB交于点D.
(Ⅰ)求点D的坐标;
(Ⅱ)当△ABC的面积大于1时, 求实数a的取值范围.
21、设a>0且a≠1,![]() (x≥1)
(x≥1)
(Ⅰ)求函数f(x)的反函数f-1(x)及其定义域;
(Ⅱ)若![]() ,求a的取值范围。
,求a的取值范围。
22. 已知函数![]() =
=![]() ,在
,在![]() 处取得极值2。
处取得极值2。
(1)求函数![]() 的解析式;
的解析式;
(2)![]() 满足什么条件时,区间
满足什么条件时,区间![]() 为函数
为函数![]() 的单调增区间?
的单调增区间?
(3)若![]() 为
为![]() =
=![]() 图象上的任意一点,直线
图象上的任意一点,直线![]() 与
与![]() =
=![]() 的图象切于
的图象切于![]() 点,求直线
点,求直线![]() 的斜率的取值范围。
的斜率的取值范围。
 南昌十六中2006届高三数学周考试卷(11) 考试时间:2005-12-08
南昌十六中2006届高三数学周考试卷(11) 考试时间:2005-12-08
![]()
| 题号 | 一 | 二 | 三 | 总分 | |||||
| 得分 | 17 | 18 | 19 | 20 | 21 | 22 | |||
|
|
|
|
|
|
| ||||
一、选择题答题表:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题答题表:
13、 14、
15、 16、
三、解答题(本题17—21小题每题12分,22小题14分,共74分)
17、(本小题满分12分)
18、(本小题满分12分)
19、(本小题满分12分)
20、(本小题满分12分)
21、(本小题满分12分)
22、(本小题满分14分)
参考答案及部分解答
一、选择题(每小题5分,共60分):
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| B | D | C | C | B | D | A | D | B | A | B | D |
二、填空题(每小题4分,共16分)
13. -1 14. -5 15、[0,3-![]() ]∪[3+
]∪[3+![]() ,+∞)16、
,+∞)16、![]()
三、解答题(共74分,按步骤得分)
(17)![]() 为奇函数
为奇函数 ![]()
![]() 为偶函数
为偶函数 ![]()
![]()
从而 ![]()
![]()
(18)(Ⅰ)CN=![]() 时,MN⊥AB1; (Ⅱ)
时,MN⊥AB1; (Ⅱ)![]() .
.
19. 解:由![]() 且x≠0,故0<x<
且x≠0,故0<x<![]() ,
,
又∵f(x)是奇函数,∴f(x-3)<-f(x2-3)=f(3-x2),又f(x)在(-3,3)上是减函数,
∴x-3>3-x2,即x2+x-6>0,解得x>2或x<-3,综上得2<x<![]() ,即A={x2<x<
,即A={x2<x<![]() },
},
∴B=A∪{x1≤x≤![]() }={x1≤x<
}={x1≤x<![]() },又g(x)=-3x2+3x-4=-3(x-
},又g(x)=-3x2+3x-4=-3(x-![]() )2-
)2-![]() 知:g(x)在B上为减函数,∴g(x)max=g(1)=-4.
知:g(x)在B上为减函数,∴g(x)max=g(1)=-4.
20. 解 (Ⅰ)易知D为线段AB的中点, 因A(a, log2a ), B(a+4, log2(a+4)),
所以由中点公式得D(a+2, log2![]() ).
).
(Ⅱ)S△ABC=S梯形AA′CC′+S梯形CC′B′B- S梯形AA′B′B=…= log2![]() ,
,
其中A′,B′,C′为A,B,C在x轴上的射影.
由S△ABC=
log2![]() >1, 得0< a<2
>1, 得0< a<2![]() -2.
-2.
21. 解 (Ⅰ)![]() 当a>1时,定义域为
当a>1时,定义域为![]() 当0<a<1时,定义域为
当0<a<1时,定义域为![]()
(Ⅱ) ![]()
即![]()
即![]()
即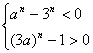 ∴
∴![]()
22解:(1)已知函数![]() =
=![]() ,
,![]() (……………2分)
(……………2分)
又函数![]() 在
在![]() 处取得极值2,
处取得极值2,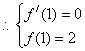 ,即
,即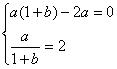
![]()
![]() (……………………5分)
(……………………5分)
(2)
由![]()
| x |
|
| (-1,1) | 1 |
|
|
| - | 0 | + | 0 |
|
|
|
| 极小值-2 |
| 极大值2 |
|
所以![]() 的单调增区间为
的单调增区间为![]() ,
(………………8分)
,
(………………8分)
若![]() 为函数
为函数![]() 的单调增区间,则有
的单调增区间,则有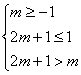
解得![]()
即![]() 时,
时,![]() 为函数
为函数![]() 的单调增区间。 (…………………10分)
的单调增区间。 (…………………10分)
(3)![]()
![]()
![]()
![]()
直线![]() 的斜率为
的斜率为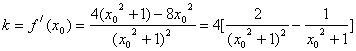 (………12分)
(………12分)
令![]() ,则直线
,则直线![]() 的斜率
的斜率![]() ,
,
![]() 。
(………………14分)
。
(………………14分)