南昌十六中2005-2006年高三周练卷（12）

　　　　　　　　　　　　　　　　 2005-12-15

一、　　　　　　 选择题:（本题每小题5分，共60分）

1. 已知集合A =，且BA，则集合B的个数为　（　　）

　　A．3个　　　　　　　　B．4个　　　　　　　　 C．8个　　　　　　　　D．16个

2．设数列是等差数列，且，是数列的前项和，则（　 ）

A、　 B、　 C、　 D、

3．若的终边所在象限是　　　　　　　　　　　  (　 )

A．第一象限　　　　　　B．第二象限　　　　　　C．第三象限　　　　　　D．第四象限

4．已知f (x)＝x⁵＋ax³＋bx－8，且f (－2)＝10，那么f (2)等于（　）。

A　10  B　－10　C　－18　D　－26

5.函数的反函数是　　　　　（　）

　　　 A．y=x²－2x+2(x<1)　　　　　　　　　　　　　　　　 B．y=x²－2x+2(x≥1)

　　　 C．y=x²－2x　(x<1)　　　　　　　　　　　　　　　　 D．y=x²－2x　(x≥1)

6.已知函数若,则的值（　）　　　　　　

A．>0　B．<0　　 C．=0　　　 D．与a的关

7、已知函数的导数为且图象过点（0，－5），当函数取得极小值－6时，x的值应为(　　 )　　　　　　　　　

A．0 　　　　　　 B．－1　　　　　　C．±1　　　　　　D． 1

8、设函数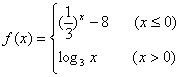，若f（a）＞1，则实数a的取值范围是(　　)

A．　 B．∪　 C．（3，+∞）　D．∪（0，+∞）

9、已知等差数列｛a_n｝中，若，则(　　)　　　　

A．　　　　 B．　　　　　  C．240　　　　 D．360

10. 图中的曲线对应的函数解析式是　　　　　　　　　　　　　　　　　　

A．　　　 　　B．

C．　　　　　 D．

11．定义在R上的偶函数满足，且在[－3，－2]上是减函数，是钝角三角形的两个锐角，则下列不等式关系中正确的是　　（　　）

　　　 A．　　　　　　　　　　　　 B．

　　　 C．　　　　　　　　　　　　D．

12．已知tana , tanb 是方程x² + 3x + 4 = 0的两根，且a , b Î (－, )，则a + b =
　　　　　　　　　　　A． 　　　B．－或　　　　　　　　　　　　　　　　　　　　　 C． 或－　　D． －

二、填空题：（本大题每小题4分，共16分）

13. 方程有解，则实数a的取值范围是_________________

14、已知函数f(x)=.则f^-－1(x－1)=_________.

15、函数f(x)=a^x (a>0, a≠1)在[1, 2]中的最大值比最小值大, 则a的值为　　 .

16、北京市为成功举办2008年奥动会，决定从2003年到2007年五年间更新市内现有的全部出租车，若每年更新的车辆数比前一年递增10%，则2003年底更新现有总车辆数的______　　　（精确到0.01）（参考数据1.1⁴=1.46,1.1⁵=1.61）

三、解答题：（本大题共6小题，共74分）

17、已知函数.(1)求其定义域和值域。(2)判断函数的奇偶性。（3）求其单调区间。

18．数列{}的前n项和为，且满足，.

　　　 （1）求{}的通项公式；

　　　 （2）求和T_n=.

19．（本小题满分12分）

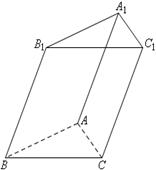
如图，三棱柱ABC—A₁B₁C₁的各棱长均为2，侧棱B₁B与底面ABC成60º的角，

且侧面ABB₁A₁⊥底面ABC，

⑴求证：AB⊥CB₁；⑵求三棱锥B₁－ABC的体积；

⑶求二面角C－AB₁－B的大小。.

20. 已知1≤x≤4, f (x)＝x²－2bx＋ (b≥1), f (x)的最小值为p，

　(1) 试用b表示p； (2) 求p的最大值，并说明此时b的取值。

21．学校为推进后勤社会化改革，与桃园新区商定：由该区向建设银行贷款500万元在桃园新区为学院建一栋可容纳一千人的学生公寓，工程于2004年初动工，年底竣工并交付使用，公寓管理处采用收费还贷偿还建行贷款（年利率5％，按复利计算），公寓所收费用除去物业管理费和水电费18万元．其余部分全部在年底还建行贷款．

（Ⅰ）若公寓收费标准定为每生每年800元，问到哪一年可偿还建行全部贷款；

（Ⅱ）若公寓管理处要在2012年底把贷款全部还清，则每生每年的最低收费标准是多少元（精确到元）．

（参考数据：lg1.7343＝0.2391，lgl.05＝0.0212，＝1.4774，＝1.5513　）

22. 设数列的前n项和为，若对于任意的 ，都有

（1）求数列的首项与递推关系式：；

（2）先阅读下面定理：“若数列有递推关系

，则数列是以A为公比的等比数列”。请你在第（1）问的基础上应用本定理，求数列的通项公式；

（3）求数列的前n项和。

南昌十六中2006届高三数学周考试卷（12）　 　　　　　　　　　　 考试时间：2005-12-15　

　　　　　　　　　　

题号	一	二	三						总分
得分			17	18	19	20	21	22

一、选择题答题表：

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案

二、填空题答题表：

　　13、　　　　　　　　　 　　 14、　　　　　　　　　 　

15、　　　　　　　　　 　　 16、　　　　　　　　　 　

三、解答题（本题17—21小题每题12分，22小题14分，共74分）

17、(本小题满分12分)

18、(本小题满分12分)

19、(本小题满分12分)

20、(本小题满分12分)

21、(本小题满分12分)

22、(本小题满分14分)

参考答案及部分解答

一、选择题（每小题5分，共60分）：

1	2	3	4	5	6	7	8	9	10	11	12
C	B	D	D	B	A	C	Ｂ	Ｄ	C	D	A

二、填空题（每小题4分，共16分）

13.  14. 　 15、0.5或1.5

三、解答题（共74分，按步骤得分）

（18）解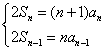： ∵ ，两式相减，得，　　 ……4分

∴ ，

∴.　　　　　　　　　　　　　　　　  ……8分

（2）

　　　 ===.…………12分

　　　　　　　　　　　　　　

19．⑴在平面ABB₁A₁中，作B₁D⊥AB，则B₁D⊥平面ABC

∴∠B₁BD为B₁B与平面ABC所成角，∴∠B₁BD＝60º

又∵△ABB₁和△ABC均为正三角形，∴D为AB中点，∴CD⊥AB，∴CB₁⊥AB

⑵易得

⑶过D作DE⊥AB₁，连CE，易证：CD⊥平面ABB₁A₁

由三垂线定理知：CE⊥AB₁，∴∠CED为二面角C－AB₁－B的平面角。

在Rt△CDE中，tan∠CED＝2，∴二面角C－AB₁－B的大小为arctan2

20. 解：(1)　f (x)＝(x－b)²－b²＋,

　当1≤b≤4且x＝b时, p＝－b²＋, 当p>4且x＝4时, p＝16－b,

　(2) 当1≤b≤4时, p＝－(b－)²＋, b＝1时，p_max＝－.

　当b>4时, p<16－×4＝－15,

　∴ b＝1时,p_max＝－.

21. 依题意，公寓2004年底建成，2005年开始使用．

　（1）设公寓投入使用后n年可偿还全部贷款，则公寓每年收费总额为1000×80（元）＝800000（元）＝80万元，扣除18万元，可偿还贷款62万元．……2分

　　依题意有　…．……4分

　　化简得．　　∴　．

　　两边取对数整理得．∴　取n＝12（年）．……5分

　　∴　到2016年底可全部还清贷款．……6分

　　（2）设每生和每年的最低收费标准为x元，因到2012年底公寓共使用了8年，

　　依题意有…．…9分

　　化简得．

　　∴　（元）

　　故每生每年的最低收费标准为992元．……12分

22（1），　

（2）A=2，B=3，

（3）