高中学生学科素质训练
高三数学测试题—函数（1）
一、选择题（本题每小题5分，共60分）
（1）若
则满足上述条件的集合M的个数是（ ）
（A）4 （B）3 （C）2 （D）1
（2）已知
则
的定义域是 （ ）
（A）[－2，2] （B）[0，2] （C）
（D）
（3）已知
，则
（ ）
（A）12 （B）8 （C）4 （D）2
（4）函数
的最大值和最小值分别是 （ ）
（A）
（B）1，－1 （C）
（D）
|
的图象是 （ ）
（6）关于x的方程
的解集是 （ ）
（A）φ （B）{－2} （C）{2} （D）{－2，2}
（7）关于
方程
的解的个数是 （ ）
（A）1 （B）2 （C）0 （D）视a的值而定
（8） 定义域为R的增函数，且值域为R+，则下列函数中为减函数的是 （ ）
（A）
（B）
（C）
（D）
（9）设
的两根是α、β，则
的值是 （ ）
（A）－4 （B）－2 （C）1 （D）3
（10）设
上的奇函数，
=
（ ）
（A）0.5 （B）－0.5 （C）1.5 （D）－1.5
（11）函数
上恒有y＞1，则a的取值范围是 （ ）
（A）
（B）
（C）（1，2） （D）
（12）函数
若a＜b＜c，且
，则下面四个式子中成立的是
（ ）
（A）
（B）
（C）
（D）
二、填空题（本题每小题4分，共16分）
（13）函数的图象与
的图象关于直线y=x对称，则
的递减区
间是 ．
（14）若是奇函数，
是偶函数，且
则=
．
（15）若=
，则的最小值是
．
（16）函数
当
时图象在直线
上方，则m的取值范围是 ．
三、解答题（本题17—21小题每题12分，22小题14分，共74分）
（17）已知a＞0，且a≠1，解不等式
（18）已知a＞0，b＞0，x∈R，且
试比较M与N的大小，并
说明理由．
（19）设
的取值范围．
（20）一家报刊摊点从报社进报的价格是每份0.12元，卖出的价格是每份0.20元，卖不掉
的报纸还可以以每份0.04元的价格退回报社，在一个月（以30天计算）里，有20天每
天可卖出400份，其余10天每天能卖出250份．但每天从报社买进的份数必须相同，
他应该每天从报社买进多少份，才能使每月所获得的利润最大？并计算他一个月最多赚
得多少元．
（21）求函数
的定义域和值域．
。
|
的图象上有两点A，B，AB//Ox轴，点M（1，m）
（m是已知实数，且
是△ABC的BC边的中点．
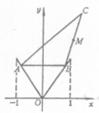
（Ⅰ）写出用B点横坐标t表示△ABC面积S的函数解析式S=f（t）；
（Ⅱ）求函数S=f（t）的最大值，并求出相应的C点坐标．
高三数学测试题参考答案
一、函数
一、1．A：由已知
则集合M的个数为22=4．
2．C：令
3．D：由
4．C：令
则
5．B：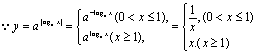
其图象为B．
6．D：由原方程得
经检验都是方程的解．
7．B：用图象法确定．
8．D：选适合题设条件的特殊函数
检验知
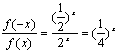为减函数．
9．A：原方程即为
因为α、β是原方程的两根，
则
10．B：
11．A 12．D
二、13．（0，1
：
而
递增，则
递减．
14．
与
联立，消去
得
15．
16．
：由
三、17．原不等式化为
∴原不等式等价于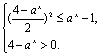
即
即
当
时，原不等式的解集是
当
时，原不等式的解集是
18．
①若
由指数函数的性质，知
②若
③若0＜a＜b，同①有N＞M． 综上所述，N＞M．
19．
（*）
将（*）代入
当且仅当
时，即x=3时等号成立．∴u的取值范围是
．
20．设每天从报社买进x份（250≤x≤400），则每月可销售（20x+10×250）份，退回报社10（x－250）份，又知卖出的报纸每份获得利润为0.08元，退回的报纸每份亏损0.08元．依题意，每月获得的利润为
在区间[250，400]上是增函数．
取得最大值，最大值为720．
21．函数
的定义域由下列不等式组确定
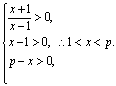
令
而抛物线
的对称轴方程为
当
故函数的值域为
当
u无最大值和最小值．但
故函数
的值域为
22．（I）依题意，设
是BC的中点．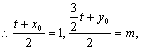
在△ABC中，AB=2t，AB边上的高
即
（Ⅱ）
若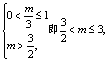
当
相应的C点坐标是
若
在区间
上是增函数，
相应的C点坐标是