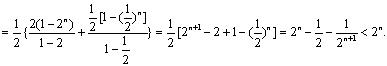高中学生学科素质训练
高三数学测试题—函数（２）
一、选择题（本题每小题5分，共60分）
（1）设
是 （ ）
（A）奇函数且在（－∞，+∞）上是增函数
（B）奇函数且在（－∞，+∞）上是减函数
（C）偶函数且在（－∞，+∞）上是增函数
（D）偶函数且在（－∞，+∞）上是减函数
（2）若将曲线
平移，使曲线上点P的坐标由（1，0）变为（2，2），则此曲线平移
后的方程是 （ ）
（A）
（B）
（C）
（D）
（3）已知
是偶函数，则函数
的图象的对称轴是 （ ）
（A）
（B）x=1 （C）
（D）
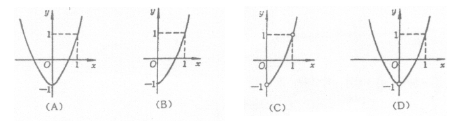
（4）方程
的图象是 （ ）
|
（5）
则有 （ ）
（A）
（B）
（C）
（D）
（6）设函数
的图象与
的图象关于直线
对称，
那么
值等于 （ ）
（A）－1 （B）－2 （C）
（D）
（7）设全集I=R，
那么
集合
应为 （ ）
（A）
（B）
（C）
（D）
（8）函数
的最小值为 （ ）
（A）
（B）
（C）
（D）不存在
（9）某工厂生产两种成本不同的产品，由于市场销售发生变化，A产品连续两次提价20%，
同时B产品连续两次降价20%，结果都以每件23.04元售出，此时厂家同时出售A、B
产品各一件，盈亏情况是 （ ）
（A）不亏不赚 （B）亏5.92元 （C）赚5.92元 （D）赚28.96元
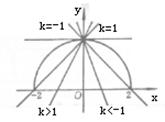
（10）若关于x的方程
只有一个实数根，则k的值为 （ ）
（A）k=0 （B）k=0或k＞1
（C）k＞1或k＜－1 （D）k=0或k＞1或k＜－1
（11）在直角坐标系中，已知过原点O的一条直线与函数
的图象交于A、B两点，
分别过A、B作x轴的垂线与
的图象交于C、D两点，可以证明直线AB与
直线CD相交，设交点为P，给出4个命题：①AB的斜率小于CD的斜率 ②点P与点
O相异 ③AB的斜率大于CD的斜率 ④点P与点O相同，其中正确的是 （ ）
（A）①④ （B）②③ （C）①② （D）③④
（12）函数存在反函数
，把的图象在直角坐标平面中绕原点按顺
时针旋转90°后得到的函数图象是 （ ）
（A）
（B）
（C）
（D）
二、填空题（本题每小题4分，共16分）
（13）函数
的定义域是
，值域是
．
（14）已知函数
= ．
（15）1992年底世界人口达到54.8亿，若人口的年平均增长率为x%，2000年底世界人口
数为y（亿），那么y与x的函数关系式是 ．
（16）某食品厂生产一批容积为1000cm3的圆柱形封闭罐头盒，若要所用的铁皮最少，罐头
盒底半径与高的比应是 ．
三、解答题（本题17—21小题每题12分，22小题14分，共74分）
（17）已知
求证对任意
（18）求函数
的定义域．
（19）已知
（Ⅰ）确定k的值；
（Ⅱ）求
的最小值及对应的x值．
（20）在商店买一种商品，大包装的比小包装的合算．如某种牙膏60克装的每支1.15元，
150克装的每支2.50元，二者单位重量的价格比为1.15∶1．牙膏的价格是由生产牙膏
的成本、包装成本及运输成本等决定的．假设忽略运输成本，并假设生产成本与牙膏（不
包括牙膏皮）重量成正比，包装成本与牙膏壳的表面积成正比，请你确定一支180克装
的牙膏的合理价格（参考数据：
（21）已知
的图象过点（m－2，0），m∈R，设g（x）=
问是否存在实数p（p＜0
，使F（x）在（－∞，―3）
上是减函数，在[―3，0）上是增函数，并证明你的结论．
（22）设
（Ⅰ）求
的定义域、值域及其反函数
（Ⅱ）设
试比较
的大
小，并证明对一切自然数n都有
高三数学测试题参考答案
二、函数
一、A：
由于
故F（x）是奇函数。用定义法不难证明F（x）在R上是增函数．
2．C：由（1，0）
（2，2），知曲线
向右平移1个单位，再向上平移2个单位，则
．
3．D：
是偶函数，图象关于y轴对称，又
图象向右平移
个单位得
的图象，因此
的图象的对称轴是
4．C：由已知方程得
亦可用特殊法检验．
5．B：由
的图象关于x=1对称，由此得b=2．所以，
在
时递增，故
6．B：由
7．D 8．C：由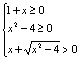
得函数的定义域为
又函数在定义域上是增函数，则
9．B：设产品A、B原价分别为xA和xB元，依题意得
解得
而现售价为
（元），因此亏52－46.08=5.92元．
10．D：用图象法．设
在同一直角坐标系中作出函数的图象分别为原点为圆心，2为半径的上半圆与过点（0，2）的直线（如图）．直线y=kx+2与半圆
只有一个交点时，k=0或
|
11．A 12．C
二、13．[1，3]，
14．0：由
得
即
15．
16．1∶2：设圆柱底面半径为rcm，高为hcm，根据题意，
又
当且仅当
三、17．∵对任意x＞0，总有
从而总有
若证
只要证明
是偶函
数即可．
的定义域是
∴
是偶函数．∵对任意x＞0时，总有
是偶函数，
那么当
18．为使
有意义，必须且只需
已知b＞0，故
恒成立，
若k≤0，则当
的定义域为R．
若k＞0，当a＞b，即
的定义域为
当a＜b，即
时，
的定义域为（－∞,
|
由②得 
代入①解得k=2．
（Ⅱ）
当
时取等号．
时取等号．
即
当
取最小值．
20．设牙膏每克价x元（不计包装），则180克装的牙膏价格为180x+包装成本，又60克装的包装成本为
1.15―60x，150克装的包装成本为2.50－150x．
解得
（元） ∴60克装的包装成本=1.15－60x=0.58(元)．
又设180克装的包装成本为y，则
∴180克装的牙膏价格应为180x+y=2.91（元）
21．
方程有实根△≥0．
解得
则
假设存在实数p＜0使F（x）满足条件，则
时，F（x）为减函数，
只需
① 又
为增函数，
同法可得
②
由①、②知存在实数
满足条件．
22．（I）由
故函数的定义域为：
的值域为：当a＞1时，
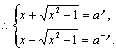
故
（Ⅱ）
