高中学生学科素质训练
高三数学测试题—三角函数（３）
一、选择题（本题每小题5分，共50分）
（1）已知
则有 （ ）
（A）
（B）
（C）
（D）
（2）已知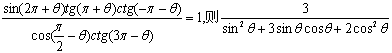
的值是（ ）
（A）1 （B）2 （C）3 （D）6
（3）设
（ ）
（A）
（B）
（C）
（D）
（4）由函数
与函数y=2形成的封闭图形的面积是 （ ）
（A）2 （B）4 （C）2π （D）4π
（5）
是奇函数，当
的表达式是（ ）
（A）
（B）
（C）
（D）
（6）设
= （ ）
（A）3 （B）4 （C）5 （D）6
（7）如果
成立的θ所在区间是 （ ）
（A）
（B）
（C）
（D）
（8）已知函数
的最小正周期不大于2，则正整数k的最小正值应该是
（ ）
（A）10 （B）11 （C）12 （D）13
（9）当
时，函数
的
（ ）
（A）最大值是1，最小值是－1 （B）最大值是1，最小值是
（C）最大值是2，最小值是－2 （D）最大值是2，最小值是－1
（10）把函数
的图象向右平移
个单位所得图象关于y轴对称，则的最
小正值是 （ ）
（A）
（B）
（C）
（D）
二、填空题（本题每小题4分，共16分）
（11）已知
的终边上，则角α的弧度数是
．
（12）若
是第
象限的角．
（13）设α、β在同一象限，且
则α、β的终边
所在的象限是第 象限。
（14）将函数
的图象上所有点的横坐标伸长到原来的2倍，使纵坐标不变，然后再
将图象沿x轴向右平移π个单位，所得的图象对应的解析式是 ．
三、解答题（本题每小题14分，共8４分）
15．求值
16．证明下列恒等式：
（1）
（2）
17．（1）求函数
的定义域和值域；
（2）求函数
的单调区间．
18．求下列函数的最大值与最小值，并求对应的x值．
（1）
（2）
19．作函数
位于区间[
]上的图象．
20．已知函数在定义域
上为减函数，且能使
对于任意的x∈R成立．求m的取值范围．
高三数学测试题参考答案
三、三角函数
一、1．D
解：
即
综上所述：所求的范围是
∴选D．
2．A 解：题设条件可化为：
∴选A．
3．C 解：原式
∴选C．
4．D 提示利用割补法求面积，
5．C 解：设
，则
对于任意的
是奇函数，
∴选C．
6．
也即
①
又
即
也即
②
①+②得：
7．C 解：要
有意义，
、π、
若
但这时，
若
若
这时，
若
、sinθ、tgθ、ctgθ＜0，综上所述，能使原式成立的
∴选C．
8．D 解：由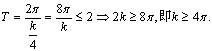
∴适合原题条件的最小正整数k为13．∴选D．
9．D 提示：
利用图象可得答案D．
10．B 解：向右平移个单位所得的图象解析式为
∵这时图象关于y轴对称，
即
∴
∴适合题意的
．∴选B．
二、11．解：
12．解：
则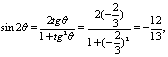
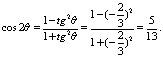
13．解：
在各象限为减函数，
由题设可知，
为减函数，
也同为减函数，∴α、β同属第二象限．
14．解：将的图象上所有点的横坐标伸长到原来的2倍，而纵坐标不变，得到的图象是
的图象；再沿x轴向右平移π个单位得到的图象是
的图象．
三、15．解：
， 
∴原式
16．（1）证明：左边
原式成立．
（2）左边
原式成立．
17．（1）解：要使原式成立，必须：
即所求的定义域为：
由题设可知：
为实数，∴△≥0，即
∴所求函数的值域为
（2）
为增函数．
∴所以所求的函数增区间为
其减区间为
18．（1）解：
根据二次函数的性质：
当
时，即当
时，
由于
不存在最大值．
（2）
总成立．
有最小值时，y有最大值；而当
有最大值时，y有最小值．
由二次函数性质可知：当
这时，
当
|
|
上的图象为：
20．解：在定义域上为减函数，
|
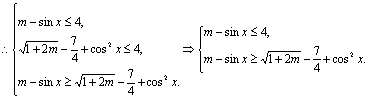
由①得：
对于任意的
，上式总成立，必须
即可
由②得：
∴对于任意的x∈R，要②总成立，只须
上式要成立，必须：
综上所述，当
时，对于任意的x，原题总成立．