巢 湖 市 六 中 高 三 第 二 次 月 考 试 卷
数学试题（理科）
一、选择题：（本大题共60分，每小题5分，共12小题）
1．
若集合
，
，则
（ ）
A．
B．
C．
D．
2．
已知
不等式
的解集为
，
是减函数，则
是
的（ ）
A．充分非必要条件 B．必要非充分条件 C．充要条件 D．既不充分也不必要条件
3．
若
，则
的值为（ ）
A．
B．
C．
D．
4．
函数
的定义域为（ ）
A．
B．
C．
D．
5．
函数
的反函数是（ ）
A．
（
） B．
（）
C．
（） D．
（）
6．
设
，
，
（
），则
，
，
的大小关系是（ ）
A．
B．
C．
D．
7．
已知
在上为增函数，则（ ）
A．
B．
C．
D．
8．
已知函数
的反函数
，则
等于（ ）
A．
B．
C．
D．
9．
以
，
，
为边长围成三角形，下述结论正确的是（ ）
A．不能围成三角形 B．能围成一个锐角三角形
C．能围成一个钝角三角形 D．能围成一个直角三角形
10．
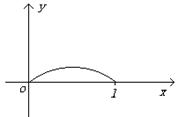已知函数（
）的图象是一段圆弧如图，若
，则（ ）
A．
B．
C．
D．前三个判断都不正确
11．
已知
，并且
，
是方程
的两根，则实数，，，的大小关系可能是（ ）
A．
B．
C．
D．
12．
若函数（），满足
，且
时
，则函数的图象与函数
的图象的交点的个数是（ ）
A．3 B．4 C．6 D．8
二、填空题：（本大题共16分，每小题4分，共4小题）
13．
若函数
，
的图象关于直线
对称，则
_______；
14．
设函数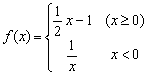
，若
，则实数的取值范围是_________；
15．
对任意函数
，
，在其定义域内，规定
，若
，
，则
的最大值为___________；
16． 给出下列四个命题：
（1）函数
（且
）与函数
的定义域相同；
（2）函数
与
的值域相同；
（3）函数
与
都是奇函数；
（4）函数
与
在区间
上都是增函数。
其中正确命题的序号是__________（把你认为正确的命题序号都填上）。
巢 湖 市 六 中 高 三 第 二 次 月 考 试 卷
数学试题（理科）
班级______________ 姓名_________________ 得分__________________
一、选择题：（本大题共60分，每小题5分，共12小题）
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
二、填空题：（本大题共16分，每小题4分，共4小题）
13．____________ 14．__________ 15．____________ 16．____________
三、解答题：（本大题共74分，共6小题）
17． （本小题满分12分）
设命题函数
是减函数；命题不等式
的解集为，如果
且
为假命题，或为真命题，求的取值范围。
18． （本小题满分12分）
已知
（且）。
（1）求与
的表示式及其定义域；（2）解关于
的不等式
。
19． （本小题满分12分）
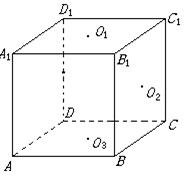如图，正方体
中，
为
的中点，
，
，
分别为面
，面
，面
的中心。（1）求证：
；（2）求异面直线
与
所成的角。
20． （本小题满分12分）
已知函数
（且
）
（1）求的单调区间；
（2）当
时，经过函数的图象上任意一点的切线的倾斜角
总在区间
范围内，试求实数的取值范围。
21． （本小题满分12分）
已知函数
（）的图象关于原点对称，，为实常数。（1）求，的值；（2）试用单调性定义证明在区间
上是单调函数；（3）当
时，不等式
恒成立，求实数的取值范围。
22． （本小题满分14分）
定义在
上的函数，对任意的
都有
，当且仅当时，
成立。
（1）设，求证：
；
（2）设
，若
，比较
，
的大小；
（3）解不等式
（
）。