巢 湖 市 六 中 高 三 第 二 次 月 考 试 卷
数学试题(文科)
一、选择题:(本大题共60分,每小题5分,共12小题)
1.
函数![]() 的定义域为( )
的定义域为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2. 下列函数中,值域为(0,+∞)的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.
若集合![]() ,
,![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.
函数![]() ,则
,则![]() 的值是( )
的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 或
或![]()
5.
已知![]() 不等式
不等式![]() 的解集为
的解集为![]() ,
,![]()
![]() 是减函数,则
是减函数,则![]() 是
是![]() 的( )
的( )
A.充分非必要条件 B.必要非充分条件 C.充要条件 D.既不充分也不必要条件
6.
已知二次函数![]() 在区间
在区间![]() 上有最小值
上有最小值![]() ,则下列关系式中一定成立的是( )
,则下列关系式中一定成立的是( )
A.![]() 或
或![]() B.
B.![]()
C.![]() 或
或![]() D.
D.![]()
7.
已知![]() 是奇函数,
是奇函数,![]() 是偶函数,且
是偶函数,且![]() ,则
,则![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.
设![]() ,
,![]() ,
,![]() ,则
,则![]() 、
、![]() 、
、![]() 的大小关系为( )
的大小关系为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.
函数![]() 在区间
在区间![]() 上的最大值是( )
上的最大值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.
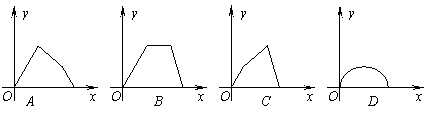
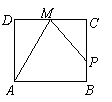 如图,点
如图,点![]() 在边长为
在边长为![]() 1的正方形
1的正方形![]() 边上运动,设点
边上运动,设点![]() 是
是![]() 边的中点,当点
边的中点,当点![]() 沿
沿![]() 运动时,点
运动时,点![]() 经过的路程记为
经过的路程记为![]() ,
,![]() 的面积为
的面积为![]() ,则函数
,则函数![]() 的图象只可能是( )
的图象只可能是( )
11.
已知![]() 的关系是( )
的关系是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.
若函数![]() (
(![]() ),满足
),满足![]() ,且
,且![]() 时
时![]() ,则函数
,则函数![]() 的图象与函数
的图象与函数![]() 的图象的交点的个数是( )
的图象的交点的个数是( )
A.3 B.4 C.6 D.8
二、填空题:(本大题共16分,每小题4分,共4小题)
13.
函数![]() (
(![]() 且
且![]() )的反函数的图像必过定点
;
)的反函数的图像必过定点
;
14.
设函数![]() (其中n∈N+),k是
(其中n∈N+),k是![]() 的小数点后的第n位数字,
的小数点后的第n位数字,![]() =3.…例如
=3.…例如![]() , 则
, 则![]() = ;
= ;
15.
设![]() 是偶函数,则
是偶函数,则![]() 的值为
;
的值为
;
16.
设![]() 是定义在
是定义在![]() 上的奇函数,且
上的奇函数,且![]() ,给出下列结论:
,给出下列结论:
(1)![]() ;
;
(2)![]() 为周期为
为周期为![]() 的函数;
的函数;
(3)![]() 的图象关于直线
的图象关于直线![]() 对称;
对称;
(4)![]() 图象关于点(2,0)对称。其中正确的结论的序号为________。
图象关于点(2,0)对称。其中正确的结论的序号为________。
巢 湖 市 六 中 高 三 第 二 次 月 考 试 卷
数学试题(文科)
班级______________ 姓名_________________ 得分__________________
一、选择题:(本大题共60分,每小题5分,共12小题)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
二、填空题:(本大题共16分,每小题4分,共4小题)
13.____________ 14.__________ 15.______________ 16.____________
三、解答题:(本大题共74分,共6小题)
17. (本小题满分12分)
已知![]() ,当
,当![]() 时,求
时,求![]() 的最大值和最小值及相应的
的最大值和最小值及相应的![]() 的值 .
的值 .
18. (本小题满分12分)
设命题![]() 函数
函数![]() 是减函数;命题
是减函数;命题![]() 不等式
不等式![]() 的解集为
的解集为![]() ,如果
,如果![]() 且
且![]() 为假命题,
为假命题,![]() 或
或![]() 为真命题,求
为真命题,求![]() 的取值范围。
的取值范围。
19. (本小题满分12分)
某蛋糕厂生产某种蛋糕的成本为40
元/个,出厂价为60元/,日销售量1000个,为适应市场需求,计划提高蛋糕档次,适度增加成本,若每个蛋糕成本增加的百分率为![]() ,则每个蛋糕的出厂价相应提高的百分率为
,则每个蛋糕的出厂价相应提高的百分率为![]() ,同时预计日销售量增加的的百分率为
,同时预计日销售量增加的的百分率为![]() ,已知: 日利润= (出厂价-成本)
,已知: 日利润= (出厂价-成本)![]() 日销售量 ,且设增加成本后的日利润为
日销售量 ,且设增加成本后的日利润为![]() .
.
(1)写出![]() 与
与![]() 的函数关系:
的函数关系:
(2)为使日利润有所增加,问![]() 应在什么范围内?
应在什么范围内?
20. (本小题满分12分)
已知函数![]() (
(![]() )的图象关于原点对称,
)的图象关于原点对称,![]() ,
,![]() 为实常数。(1)求
为实常数。(1)求![]() ,
,![]() 的值;(2)试用单调性定义证明
的值;(2)试用单调性定义证明![]() 在区间
在区间![]() 上是单调函数;(3)当
上是单调函数;(3)当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围。
的取值范围。
21. (本小题满分12分)
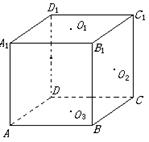 如图,正方体
如图,正方体![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() ,
,![]() 分别为面
分别为面![]() ,面
,面![]() ,面
,面![]() 的中心。(1)求证:
的中心。(1)求证:![]() ;(2)求异面直线
;(2)求异面直线![]() 与
与![]() 所成的角。
所成的角。
22. (本小题满分14分)
已知![]() 在
在![]() 上有定义,
上有定义,![]() ,且满足
,且满足![]() 有
有![]()
(Ⅰ)证明:![]() 在
在![]() 上为奇函数;
上为奇函数;
(Ⅱ)对数列![]() ,
,![]() ,求
,求![]() ;
;
(Ⅲ)求证![]()