高三数学第一学期期末试卷
(试卷满分为150分,考试时间为120分钟)
一.选择题(每题5分,共60分)。
1、已知集合![]() ,则集合
,则集合![]() =( )
=( )
A.{![]() } B.{
} B.{![]() }
}
C.{![]() } D.{
} D.{![]() }
}
2、设实数a∈[-1,3], 函数f(x)=x2-(a+3)x+2a,当f(x)>1时,实数x的取值范围是( )
A、[-1,3] B、(-5,+∞) C、(-∞,-1)∪(5,+∞) D、(-∞,1)∪(5,+∞)
3、已知函数f(x)=![]() 在区间[2,+∞)是减函数,则实数a的取值范围是( )
在区间[2,+∞)是减函数,则实数a的取值范围是( )
A、(-∞,4) B、(0,12) C、(-4,4) D、(0,4)
4、已知函数![]() ,那么f-1(1)的值等于( )。
,那么f-1(1)的值等于( )。
A、0 B、-2 C、![]() D、
D、![]()
5、将y=2x的图象( ),再作关于直线y=x对称的图象,可得函数y=log2(x+1)的图象。
A、先向左平移一个单位 B、先向右平移一个单位
C、先向上平移一个单位 D、先向下平移一个单位
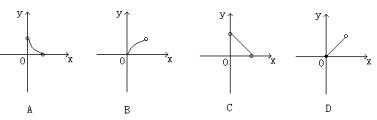
6、一个棱锥被平行于底面的截面截成一个小棱锥和一个棱台(用一个平行于棱锥底面的平面去截棱锥,底面和截面之间的部分叫棱台),若小棱锥的体积为y,棱台的体积为x,则y关于x的函数图象大致形状为( )。
7、已知数列![]() ,那么“对任意的
,那么“对任意的![]() ,点
,点![]() 都在直线
都在直线![]() 上”是“
上”是“![]() 为等差数列”的 ( )
为等差数列”的 ( )
(A)必要而不充分条件 (B)充分而不必要条件
(C)充要条件 (D)既不充分也不必要条件
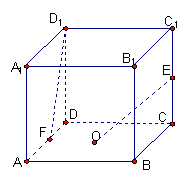
8、如图,在棱长为2的正方体![]() 中,O是底面ABCD的中心,E、F分别是
中,O是底面ABCD的中心,E、F分别是![]() 、AD的中点。那么异面直线OE和
、AD的中点。那么异面直线OE和![]() 所成的角的余弦值等于( )
所成的角的余弦值等于( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
9、若![]() 为圆
为圆![]() 的弦AB的中点,则直线AB的方程是( )
的弦AB的中点,则直线AB的方程是( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
10、函数![]() )为增函数的区间是( )
)为增函数的区间是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
11、已知向量a、b满足:a=1,b=2,a-b=2,则a+b=( )
A.1 B.![]() C.
C.![]() D.
D.![]()
12、已知函数f(x)定义域为R,则下列命题:
①y=f(x)为偶函数,则y=f(x+2)的图象关于y轴对称.
②y=f(x+2)为偶函数,则y=f(x)关于直线x=2对称.
③若函数f(2x+1)是偶函数,则f(2x)的图象关于直线 ![]() 对称.
对称.
④若f(x-2)=f(2-x),则y=f(x)关于直线x=2对称.
⑤y=f(x-2)和y=f(2-x)的图象关于x=2对称.
其中正确的命题序号是( )
A、①②④ B、①③④ C、②③⑤ D、②③④
二. 填空题(每题5分,共20分)。
13、设坐标平面内有一个质点从原点出发,沿x轴跳动,每次向正方向或负方向跳1个单位,经过5次跳动质点落在点(3,0)(允许重复过此点)处,则质点不同的运动方法共有________种(用数字作答)。
14、若![]()
![]() ,则
,则![]() 。(用数字作答)
。(用数字作答)
15、两个篮球运动员在罚球时投球的命中率为0.7和0.6,每人投篮三次,则两人都恰好进2球的概率是______。(用数字作答,精确到千分位)
16、曲线![]() 关于直线x=2对称的曲线方程是___________。
关于直线x=2对称的曲线方程是___________。
三、解答题(共70分)
17、(本题满分14分)
在ΔABC中,角A、B、C所对的边分别为a、b、c,且![]() 。
。
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)若![]() ,求bc的最大值。
,求bc的最大值。
18、(本题满分14分)
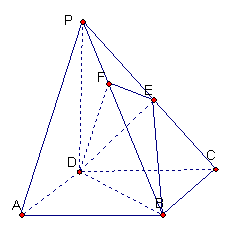
如图,在四棱锥![]() 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱![]() 底面ABCD,
底面ABCD,![]() ,E是PC的中点,作
,E是PC的中点,作![]() 交PB于点F。
交PB于点F。
(I)证明 ![]() 平面
平面![]() ;
;
(II)证明![]() 平面EFD;
平面EFD;
(III)求二面角![]() 的大小。
的大小。
19、(本题满分14分)
盒子中有大小相同的球10个,其中标号为1的球3个,标号为2的球4个,标号为5的球3个,第一次从盒子中任取1个球,放回后第二次再任取1个球(假设取到每个球的可能性都相同)。记第一次与第二次取到球的标号之和为![]() 。
。
(Ⅰ)试用列举法表示随机变量![]() 的取值集合
的取值集合![]() ;
;
(Ⅱ)分别求随机变量![]() 任取集合
任取集合![]() 中每一个值的概率。
中每一个值的概率。
20、(本题满分14分)
设a>0,![]() 是奇函数。
是奇函数。
(1)试确定a的值;
(2)试判断f(x)的反函数f-1(x)的单调性,并证明。
21、(本题满分14分)
一条斜率为1的直线l与离心率![]() 的双曲线
的双曲线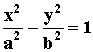 (a>0,
b>0)交于P、Q两点,直线l与y轴交于R点,且
(a>0,
b>0)交于P、Q两点,直线l与y轴交于R点,且![]() ,求直线和双曲线方程。
,求直线和双曲线方程。
 |
一.选择题( 5分 × 12 = 60 分 )
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 答案 | C | C | C | A | D | C |
| 题号 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | B | A | C | D | C |
二.填空题( 5分 × 4 = 20分 )
13、5 14、1 15、0.19 16、![]()
三、解答题(共70分)
17、(本题满分14分)
在ΔABC中,角A、B、C所对的边分别为a、b、c,且![]() 。
。
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)若![]() ,求bc的最大值。
,求bc的最大值。
解: (Ⅰ)![]() =
=![]()
=![]() =
=![]() =
= ![]()
(Ⅱ) ∵ ![]() ∴
∴ ![]() ,
,
又∵ ![]() ∴
∴ ![]() 当且仅当 b=c=
当且仅当 b=c=![]() 时,bc=
时,bc=![]() ,故bc的最大值是
,故bc的最大值是![]() .
.
18、(本题满分14分)
如图,在四棱锥![]() 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱![]() 底面ABCD,
底面ABCD,![]() ,
,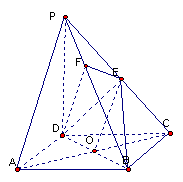 E是PC的中点,作
E是PC的中点,作![]() 交PB于点F。
交PB于点F。
(I)证明 ![]() 平面
平面![]() ;
;
(II)证明![]() 平面EFD;
平面EFD;
(III)求二面角![]() 的大小。
的大小。
方法一:
(I)证明:连结AC,AC交BD于O。连结EO。
![]() 底面ABCD是正方形,
底面ABCD是正方形,![]() 点O是AC的中点
点O是AC的中点
在![]() 中,EO是中位线,
中,EO是中位线,![]() 。
。
而![]() 平面EDB且
平面EDB且![]() 平面EDB,
平面EDB,
所以,![]() 平面EDB。
平面EDB。
(II)证明:![]() 底在ABCD且
底在ABCD且![]() 底面ABCD,
底面ABCD,![]()
![]() ①
①
同样由![]() 底面ABCD,得
底面ABCD,得![]()
![]() 底面ABCD是正方形,有
底面ABCD是正方形,有![]() 平面PDC
平面PDC
而![]() 平面PDC,
平面PDC,![]() ② ………………………………6分
② ………………………………6分
由①和②推得![]() 平面PBC
平面PBC
而![]() 平面PBC,
平面PBC,![]()
又![]() 且
且![]() ,所以
,所以![]() 平面EFD
平面EFD
(III)解:由(II)知,![]() ,故
,故![]() 是二面角
是二面角![]() 的平面角
的平面角
由(II)知,![]()
设正方形ABCD的边长为![]() ,则
,则![]()
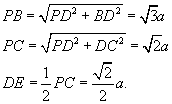
在![]() 中,
中,
![]()
在![]() 中,
中,
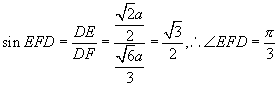
所以,二面角![]() 的大小为
的大小为![]()
方法二:如图所示建立空间直角坐标系,D为坐标原点。设![]()
(I)证明:连结AC,AC交BD于G。连结EG。
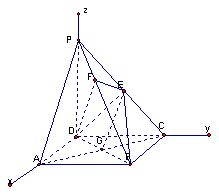 依题意得
依题意得![]()
![]() 底面ABCD是正方形,
底面ABCD是正方形,
![]()
![]() 是此正方形的中心,
是此正方形的中心,
![]() 故点G的坐标为
故点G的坐标为![]() 且
且
![]()
![]() 。这表明
。这表明![]() 。
。
而![]() 平面EDB且
平面EDB且![]() 平面EDB,
平面EDB,![]() 平面EDB。
平面EDB。
(II)证明:依题意得![]() 。又
。又![]() 故
故
![]()
![]()
由已知![]() ,且
,且![]() 所以
所以![]() 平面EFD。
平面EFD。
(III)解:设点F的坐标为![]() 则
则
![]()
从而![]() 所以
所以
![]()
由条件![]() 知,
知,![]() 即
即
![]() 解得
解得 ![]() 。
。
![]() 点F的坐标为
点F的坐标为![]() 且
且
![]()
![]()
即![]() ,故
,故![]() 是二面角
是二面角![]() 的平面角。
的平面角。
![]() 且
且
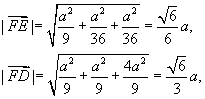
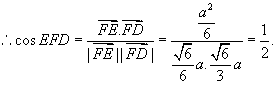
![]()
所以,二面角![]() 的大小为
的大小为![]()
19、(本题满分14分)
盒子中有大小相同的球10个,其中标号为1的球3个,标号为2的球4个,标号为5的球3个,第一次从盒子中任取1个球,放回后第二次再任取1个球(假设取到每个球的可能性都相同)。记第一次与第二次取到球的标号之和为![]() 。
。
(Ⅰ)试用列举法表示随机变量![]() 的取值集合
的取值集合![]() ;
;
(Ⅱ)求随机变量![]() 任取集合
任取集合![]() 中每一个值的概率。
中每一个值的概率。
解:
(Ⅰ)由题意可得,随机变量![]() 的取值集合是
的取值集合是![]() ={2、3、4、6、7、10}。
={2、3、4、6、7、10}。
(Ⅱ)随机变量![]() 取集合
取集合![]() ={2、3、4、6、7、10}中的每一个值时,其概率如下:
={2、3、4、6、7、10}中的每一个值时,其概率如下:
|
| 2 | 3 | 4 | 6 | 7 | 10 |
| P( | 0.09 | 0.24 | 0.16 | 0.18 | 0.24 | 0.09 |
20、(本题满分14分)
设a>0,![]() 是奇函数。
是奇函数。
(1)试确定a的值;
(2)试判断f(x)的反函数f-1(x)的单调性,并证明。
解:
(1)∵ f(x)为奇函数, ∴ f(x)+f(-x)=0
即![]() 对定义域内x均成立,
对定义域内x均成立,
解得a=1,即 ![]() 。
。
(2)由![]() 得
得 ![]() , ∴
, ∴ ![]() ,
,
∴ ![]() , ∴ f-1(x)在定义域内为增函数,
, ∴ f-1(x)在定义域内为增函数,
当任取定义域内x1,x2且x1<x2时,
因 ![]() 得
得![]() ,
,
则![]() ,
,
∴ f-1(x1)<f-1(x2),即f-1(x)为增函数。
21、(本题满分14分)
一条斜率为1的直线l与离心率![]() 的双曲线
的双曲线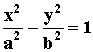 (a>0,
b>0)交于P、Q两点,直线l与y轴交于R点,且
(a>0,
b>0)交于P、Q两点,直线l与y轴交于R点,且![]() ,求直线和双曲线方程。
,求直线和双曲线方程。
解:∵ ![]() , ∴ b2=2a2,∴ 双曲线方程可化为2x2-y2=2a2,
, ∴ b2=2a2,∴ 双曲线方程可化为2x2-y2=2a2,
设直线方程为 y=x+m,
由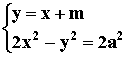 得 x2-2mx-m2-2a2=0,
得 x2-2mx-m2-2a2=0,
∴ Δ=4m2+4(m2+2a2)>0
∴ 直线一定与双曲线相交。
设P(x1, y1), Q(x2, y2), 则x1+x2=2m, x1x2=-m2-2a2,
∵ ![]() ,
, ![]() ,
,
∴ ![]() , ∴
, ∴ ![]()
消去x2得,m2=a2,
![]() =x1x2+y1y2=x1x2+(x1+m)(x2+m)
=x1x2+y1y2=x1x2+(x1+m)(x2+m)
=2x1x2+m(x1+x2)+m2=m2-4a2=-3
∴ m=±1, a2=1, b2=2.
直线方程为y=x±1,双曲线方程为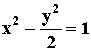 。
。