高考高三数学寒假作业

高三数学寒假作业（1）

班级　　　　　 　 姓名 　　　　　 　 学号　　　　　

家长签字　　　　　 　完成日期　　　　　　  　 

1、若函数，则该函数在上是　　　　　　　　　 （　　）

A．单调递减无最小值　　　　　　　　  B．单调递减有最小值

C．单调递增无最大值　　　　　　　　  D．单调递增有最大值

2、已知集合，，则等于（　）

A．　　　　　　　 B．

C．　　　　　　  D．

3、用个不同的实数可得到个不同的排列，每个排列为一行写成一个行的数阵。对第行，记，。例如：用1，2，3可得数阵如图，由于此数阵中每一列各数之和都是12，所以，，那么，在用1，2，3，4，5形成的数阵中，等于　　　　　　　　　　 （　 ）

A．—3600　　　　  B．1800　　　　  C．—1080　　　　  D．—720

4、函数的图象与直线有且仅有两个不同的交点，则的取值范围是__________。

5、有两个相同的直三棱柱，高为，底面三角形的三边长分别为。用它们拼成一个三棱柱或四棱柱，在所有可能的情形中，全面积最小的是一个四棱柱，则的取值范围是__________。

6、已知抛物线的焦点为F，A是抛物线上横坐标为4、且位于轴上方的点，A到抛物线准线的距离等于5。过A作AB垂直于轴，垂足为B，OB的中点为M。（Ⅰ）求抛物线方程；

（Ⅱ）过M作，垂足为N，求点N的坐标；

（Ⅲ）以M为圆心，MB为半径作圆M，当是轴上一动点时，讨论直线AK与圆M的位置关系。

高三数学寒假作业（2）

班级　　　　　 　 姓名 　　　　　 　 学号　　　　　

家长签字　 　　　　　完成日期　　　　　　  　 

1、为了得到函数的图象，只需把函数的图象上所有的点（　　）

　　　 A．向右科移3个单位长度，再向下平移1个单位长度

　　　 B．向左平移3个单位长度，再向下平移1个单位长度

　　　 C．向右平移3个单位长度，再向上平移1个单位长度

　　　 D．向左平移3个单位长度，再向上平移1个单位长度

2、对任意的锐角，下列不等关系中正确的是　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　　 B．

　　　 C．　　　　　　　 D．

3、设椭圆的两个焦点分别为F_1、、F₂，过F₂作椭圆长轴的垂线交椭圆于点P，若△F₁PF₂为等腰直角三角形，则椭圆的离心率是　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　  B．　　　  C．　 　　　　　D．

4、已知在△ABC中，∠ACB=90°，BC=3，AC=4，P是AB上的点，则点P到AC、BC的距离乘积的最大值是　　　　　　

5、对于函数定义域中任意的，有如下结论：

　　　 ①；　　　　　　 ②；

　　　 ③　　　　　　　　　　　　　　④

时，上述结论中正确结论的序号是　　　　　　  .

6、假设某市2004年新建住房面积400万平方米，其中有250万平方米是中低价房。预计在今后的若干年内，该市每年新建住房面积平均比上一年增长8%。另外，每年新建住房中，中低价房的面积均比上一年增加50万平方米。那么，到哪一年底，

（Ⅰ）该市历年所建中低价层的累计面积（以2004年为累计的第一年）将首次不少于4780万平方米？

（Ⅱ）当年建造的中低价房的面积占该年建造住房面积的比例首次大于85%？

高三数学寒假作业（3）

班级　　　　　 　 姓名 　　　　　 　 学号　　　　　

家长签字　　　　　 　完成日期　　　　　　  　 

1、设I为全集，S₁、S₂、S₃是I的三个非空子集且S₁∪S₂∪S₃=I，则下面论断正确的是（　 ）

　　　 A．_IS_I∩（S₂∪S₃）=　　　　　　　　　　　　B．S₁（_I S₂∩ _IS₃）

　　　 C． _IS_I∩　_IS₂ ∩　_IS₃=　　　　　　　　　　　　　D．S₁（ _I S₂∪　_IS₃）

2、已知双曲线的焦点为F₁、F₂，点M在双曲线上且则点M到x轴的距离为　　　　　　　 （　　）

　　　 A．　　 　　　　　　 B．　 　　　　　　　　 C．　 　　　　　　D．

3、当时，函数的最小值为　　　　  （　　）

　　　 A．2　　　　　　　　　　　　B．2　　　　　　　　　C．4　　　　　　　　　　　　D．4

4、若正整数m满足10^m－1<2⁵¹²<10^m，则m=　　　　  .(lg2=0.3010)

5、正方体ABCD—A′B′C′D′中，过对角线BD′的一个平面交AA′于E，交CC′

于F，

　　　 ①四边形BF D′E一定是平行四边形；

　　　 ②四边形BF D′E有可能是正方形；

　　　 ③四边形BF D′E在底面ABCD的投影一定是正方形；

　　　 ④平面BF D′E有可能垂直于平面B B′D.

　　　 以上结论正确的为　　　　　　  .（写出所有正确结论的编号）

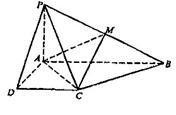6、已知四棱锥P—ABCD的底面为直角梯形，AB//DC，∠DAB=90°，PA⊥底面ABCD，且是PB的中点.

　 （Ⅰ）证明：面PAD⊥面PCD；

　 （Ⅱ）求AC与PB所成的角；

　 （Ⅲ）求面AMC与面BMC所成二面角的大小.

高三数学寒假作业（4）

班级　　　　　 　 姓名 　　　　　 　 学号　　　　　

家长签字　　　　　 　完成日期　　　　　　  　 

1、的反函数是　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　　B．

　　　 C．　　　　　　　D．

2、设的取值范围是（　 ）

　　　 A．　　　　　　　B．　　　　　　　C．　　　D．

3、在坐标平面上，不等式组所表示的平面区域面积为　　  （　　）

　　　 A．　　　　　　　　　　B．　　　　　　　　　　　C．　　　　　　　　 D．2

4、在△ABC中，已知,给出以下四个论断 　　　　　　　　。

　　　 ①tanA·cotB=1　　　　　　　　　　　　　　　　　　　 ②0<sinA+sinB≤

　　　 ③sin²A+cos²B=1　　　　　　　　　　　　　　　　　　　④cosA²+cos²B=sin²C

5、点O是三角形ABC所在平面内的一点，满足，则点

O是△ABC的　　　　  心

6、设正项等比数列的首项，前n项和为S_n，且

　 （Ⅰ）求的通项；

　 （Ⅱ）求的前n项和T_n.

高三数学寒假作业（5）

班级　　　　　 　 姓名 　　　　　 　 学号　　　　　

家长签字　　　　　 　完成日期　　　　　　  　 

1、正方体ABCD—A₁B₁C₁D₁中，P、Q、R分别是AB、AD、B₁C₁的中点. 那么，正方体的过P、Q、R的截面图形是　　 　　　 （　　）

　　　 A．三角形　　　　　　　 B．四边形　　　　　　　　C．五边形　　　　　　　 D．六边形

2、已知点A（，1），B（0，0）C（，0）.设∠BAC的平分线AE与BC相交于E，那么有等于　 　　　 （　　）

　　　 A．2　　　　　　　　　　　　B．　　　　　　　　　　　C．－3　　　　　　　　　　 D．－

3、点P在平面上作匀速直线运动，速度向量即点P的运动方向与v相同，且每秒移动的距离为v个单位）.设开始时点P的坐标为（－10，10），则5秒后点P的坐标为（　　）

　　　 A．（－2，4）　　　　　B．（－30，25）　　　 C．（10，－5）　　　　D．（5，－10）

4、在之间插入三个数，使这五个数成等比数列，则插入的三个数的乘积为　　 .

5、下面是关于三棱锥的四个命题：

　　　 ①底面是等边三角形，侧面与底面所成的二面角都相等的三棱锥是正三棱锥.

②底面是等边三角形，侧面都是等腰三角形的三棱锥是正三棱锥.

③底面是等边三角形，侧面的面积都相等的三棱锥是正三棱锥.

④侧棱与底面所成的角都相等，且侧面与底面所成的二面角都相等的三棱锥是正三棱锥.其中，真命题的编号是　　　　　　　 （写出所有真命题的编号）.

6、 已知向量和且　求的值.