素质能力检测（八）
一、选择题（每小题5分，共60分）
1.过原点的直线l与双曲线
－
=－1交于两点，则直线l的斜率的取值范围是
A.（－
，）
B.（－∞，－）∪（，+∞）
C.［－
，］
D.（－∞，－）∪［，+∞）
解析：双曲线焦点在y轴上，渐近线斜率为±，利用数形结合易得k＞或k＜ －.
答案：B
2.（2005年启东市第二次调研题）过点M（－2，0）的直线l与椭圆x2+2y2=2交于P1、P2两点，线段P1P2的中点为P，设直线l的斜率为k1（k1≠0），直线OP的斜率为k2，则k1·k2的值为
A.2 B.－2
C.
D.－
解析：设P1（x1，y1）、P2（x2，y2），中点P（x0，y0），则k1=
，k2=
=
.
将P1、P2两点坐标代入椭圆方程x2+2y2=2，相减得
=－.
∴k1·k2=·==－.
答案：D
3.（2005年黄冈市调研题）如果方程
+
=1表示双曲线，则下列椭圆中，与该双曲线共焦点的是
A.
+=1
B.+=－1
C.
+=1
D.+=－1
解析：由题意有pq>0，若p>0，q>0，则双曲线焦点位于y轴上且c2=p+q无答案，则只有p<0，q<0，焦点位于x轴上，且c2=－p－q，B答案符合.
答案：B
|
x=2cosθ，
y=sinθ（其中参数θ∈R）上的点的最短距离为
A.
B.1
C. 
D. 
解析：d=
=
=
，
dmin=.
答案：A
5.（2005年北京海淀区第一学期期末练习）已知mn≠0，则方程mx2+ny2=1与mx+ny2=0在同一坐标系下的图形可能是
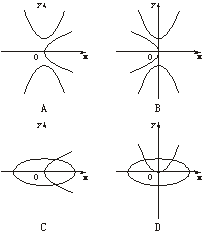
解析：由mn≠0，分m、n同号或异号讨论即得A正确.
答案：A
6.双曲线的虚轴长为4，离心率e=
，F1、F2分别是它的左、右焦点，若过F1的直线与双曲线的左支交于A、B两点，且AB是AF2与BF2的等差中项，则AB等于
A.8
B.4
C.2
D.8
解析：由题意知b=2，
=，∴a=2.
由双曲线的定义知
AF2－AF1=4，BF2－BF1=4.
∴AF2+BF2－（AF1+BF1）=8，即AB=8.
答案：A
7.若点A的坐标为（3，2），F为抛物线y2＝2x的焦点，点P在此抛物线上移动，当｜PA｜＋｜PF｜取最小值时，点P的坐标为
A.（0，0） B.（－2，－2）
C.（2，2） D.（2，0）
解析：由抛物线的定义知：过A作准线的垂线与抛物线的交点即为所求.
答案：C
8.双曲线
－
=1（mn≠0）的离心率为2，则
的值为
A.3
B. 
C.3或－
D.3或
解析：当m＞0，n＞0时，c=
，a=
，由题意
=2，解得=；
当m＜0，n＜0时，c=
＝，a=
，
=2，解得=3.
答案：D
9.已知P1（x1，y1）、P2（x2，y2）是抛物线y2＝2px（p＞0）上两个不同点，则y1·y2＝－p2是直线P1P2过焦点的
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
解析：显然当P1P2是通径时y1·y2＝－p2，设P1P2的方程为x＝ky＋b，代入y2＝2Px，知y2＝2p（ky＋b），即y2－2pky－2pb＝0，由y1y2＝－p2，b＝p，
∴P1P2：x－p＝ky，此直线过点（
，0）.
反之，若直线P1P2过焦点F（，0）易得y1y2=－p2.
答案：C
10.圆心在抛物线y2=2x上，且与x轴和该抛物线的准线都相切的一个圆的方程是
A.x2+y2－x－2y+
=0
B.x2+y2+x－2y+1=0
C.x2+y2－x－2y+1=0
D.x2+y2－x－2y－=0
解析：利用平面几何的知识及抛物线的定义易知圆的半径为1，圆心坐标为（，1），（，－1）.
答案：A
11.P是双曲线
－
=1（a＞0，b＞0）右支上一点，F1、F2分别是左、右焦点，且焦距为2c，则△PF1F2的内切圆圆心的横坐标为
A.a B.b C.c D.a+b－c
解析：利用平面几何的知识及双曲线的定义易知：△PF1F2的内切圆与x轴的切点为双曲线的右顶点.
答案：A
12.关于方程x2+2y2－ax+ay－a－1=0（a∈R）表示的椭圆，给出以下四个命题：
①椭圆的中心在一条直线上运动；
②椭圆的大小不变；
③不论a取什么值，椭圆总过两个定点；
④椭圆的离心率不变.
其中错误命题的个数是
A.3 B.2 C.1 D.0
解析：椭圆方程为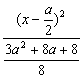
+
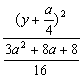=1，
故中心（
，－
）在直线y=－x上运动.
∴①成立.
离心率e=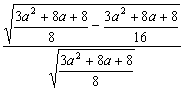
=
=
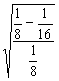（定值），故④成立.
随a的变化，
与
均变化，故②不成立.
椭圆方程又可写为（x2+2y2－1）+a（－x+y－1）=0.
|
|
x2+2y2－1=0，
－x+y－1=0，
由Δ=42－4×3＞0知方程组有两组解，故③成立.
综上知只有②错误，故选C.
答案：C
二、填空题（每小题4分，共16分）
13.（2003年北京）以双曲线
－
=1的右顶点为顶点，左焦点为焦点的抛物线的方程是____________.
解析：在双曲线－=1中，右顶点为（4，0），左焦点为（－5，0）.
由题设抛物线方程为y2=－2p（x－4）（p＞0），
且满足=4－（－5），∴p=18.
∴y2=－2×18（x－4），
即y2=－36（x－4）.
答案：y2=－36（x－4）
14.已知椭圆x2+2y2=4，则以（1，1）为中点的弦的长度为____________.
解析：依题意设弦端点为A（x1，y1）、B（x2，y2）.
分别代入椭圆方程相减得此弦的斜率k==－
=－.
∴此弦的方程为y=－x+
.代入x2+2y2=4，
整理得3x2－6x+1=0.
∴x1+x2=2，x1x2=.
∴AB=
·
=
·
=
.
答案：
15.（2005年黄冈市调研，15）在△ABC中，B（－2，0）、C（2，0）、A（x，y），给出△ABC满足的条件，就能得到动点A的轨迹方程，下面给出了一些条件及方程，请你用线把左边△ABC满足的条件及相应的右边A点的轨迹方程连起来.（错一条连线得0分）
①△ABC周长为10 a y2=25
②△ABC面积为10 b x2+y2=4（y≠0）
③△ABC中，∠A=90°
c 
+
=1（y≠0）
解析：①由AB+AC=6，得+=1（y≠0）.
②由BCy=10，得y2=25.
③由AB2+AC2=BC2，得x2+y2=4（y≠0）.
答案：①→c ②→a ③→b
16.（2004年春季上海）若平移椭圆4（x+3）2+9y2=36，使平移后的椭圆中心在第一象限，且它与x轴、y轴分别只有一个交点，则平移后的椭圆方程是_____________.
解析：由题意知椭圆的长半轴长a=3，短半轴长b=2，因椭圆与x轴、y轴只有一个交点，故椭圆与x轴、y轴相切，椭圆的中心为（3，2），所以椭圆方程为
+
=1.
答案：+=1
三、解答题（本大题共6小题，共74分）
17.（12分）（2005年北京海淀区第一学期期末练习）设椭圆+=1（a>b>0）的左焦点为F1（－2，0），左准线l1与x轴交于点N（－3，0），过点N且倾斜角为30°的直线l交椭圆于A、B两点.
（1）求直线l和椭圆的方程；
（2）求证：点F1（－2，0）在以线段AB为直径的圆上；
（3）在直线l上有两个不重合的动点C、D，以CD为直径且过点F1的所有圆中，求面积最小的圆的半径长.
（1）解：直线l：y=（x+3），
由已知c=2及
=3，
解得a2=6，∴b2=6－22=2.
∴椭圆方程为
+
=1.
|
x2+3y2－6=0， ①
y=（x+3），
②
将②代入①，整理得2x2+6x+3=0. ③
设A（x1，y1）、B（x2，y2），则x1+x2=－3，x1x2=.
方法一：k
·k
=
·
=
=
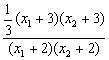
=－1，
∴F1A⊥F1B，即∠AF1B=90°.
∴点F1（－2，0）在以线段AB为直径的圆上.
方法二：
·
=（x1+2，y1）·（x2+2，y2）
=（x1+2）（x2+2）+y1y2
=x1x2+2（x1+x2）+4+［x1x2+3（x1+x2）+9］
=
x1x2+3（x1+x2）+7=0，
∴F1A⊥F1B.则∠AF1B=90°.
∴点F1（－2，0）在以线段AB为直径的圆上.
（3）解：面积最小的圆的半径长应是点F1到直线l的距离，设为r.
∴r=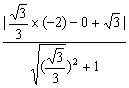
=为所求.
18.（12分）已知椭圆的焦点是F1（－
，0）和F2（，0），离心率为e=.
（1）求椭圆上的点到直线2x+3y+8=0距离的最大值；
（2）若P在椭圆上，
·
=，求△PF1F2的面积.
解：（1）设椭圆+=1，半焦距为c，则
|
|
c= a=2
a2=4，
=
a2－b2=3 b2=1.
∴椭圆方程为+y2=1.
设椭圆上的点为P（2cosθ，sinθ），
P到直线2x+3y+8=0的距离d=
=
≤
=
.
当且仅当sin（θ+
）=1时取“=”（其中tan=）.
椭圆上的点到直线2x+3y+8=0的最大值为.
（2）∵·=cos〈，〉=，
又∵
2=2+2－2·cos〈，〉，
∴PF1+PF2=4，
即12=（+）2－2·－·2=16－2·－·2
·=cos〈，〉=sin〈，〉=.
∴S△PF
F
=sin〈，〉=··=.
19.（12分）（2004年春季上海）设点P（x，y）（x≥0）为平面直角坐标系xOy中的一个动点（其中O为坐标原点），点P到定点M（，0）的距离比点P到y轴的距离大.
（1）求点P的轨迹方程，并说明它表示什么曲线；
（2）若直线l与点P的轨迹相交于A、B两点，且OA⊥OB，点O到直线l的距离为，求直线l的方程.
解：（1）∵x≥0，∴
=x+.
整理得y2=2x.
这就是动点P的轨迹方程，它表示顶点在原点，对称轴为x轴，开口向右的一条抛物线.
（2）①当直线l的斜率不存在时，由题设可知，直线l的方程是x=.
联立x=与y2=2x，可求得点A、B的坐标分别为（，
）与（，－），此时不满足OA⊥OB，故不合题意.
②当直线l的斜率存在时，可设直线l的方程为y=kx+b（其中k≠0，b≠0）.
将x=
代入y2=2x中，
并整理得ky2－2y+2b=0. ①
设直线l与抛物线的交点坐标为A（x1，y1）、B（x2，y2），则y1、y2为方程①的两个根，于是y1y2=
.
又由OA⊥OB可得x1x2+y1y2=0. ②
将x1=
，x2=
代入②并整理得y1y2+4=0，∴b+2k=0. ③
又由点O到直线l的距离为，得
=. ④
联立③④得k=1，b=－2或k=－1，b=2.
故直线l的方程为y=x－2或y=－x+2.
20.（12分）（2003年北京朝阳区模拟题）已知椭圆C：+=1（a＞b＞0）.
（1）若点P（x0，y0）是椭圆C内部的一点，求证：
+
＜1；
（2）若椭圆C：+=1（a＞b＞0）上存在不同的两点关于直线l：y=x+1对称，试求a、b满足的关系式.
（1）证明：设F1、F2为椭圆C的左、右两个焦点.∵P是椭圆C内部的一点，
∴F1P+F2P＜2a.
∴
+
＜2a.
∴（a2－c2）x02+a2y02＜a2（a2－c2）.
∴+＜1（b2=a2－c2）.
（2）解：设椭圆C上关于直线l对称的点A、B的坐标为A（x1，y1）、B（x2，y2），线段AB的中点坐标为M（xM，yM），则有
b2x12+a2y12=a2b2，
①
b2x22+a2y22=a2b2， ②
=－1， ③
yM=xM+1. ④
②－①得b2（x22－x12）+a2（y22－y12）=0，
b2（x2－x1）（x2+x1）+a2（y2－y1）（y2+y1）=0，
b2xM+a2yM=0，
把③代入上式得b2xM－a2yM=0， ⑤
由④和⑤得xM=
，yM=
，
即M（，）.
∵点M在椭圆C的内部，
∴
+
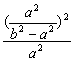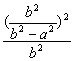＜1.
∴a2+b2＜（b2－a2）2=（a+b）2（a－b）2.
a、b应满足的不等式为a2+b2＜（a+b）2（a－b）2.
21.有点难度哟！
（12分）（2004年全国Ⅱ，21）给定抛物线C：y2=4x，F是C的焦点，过点F的直线l与C相交于A、B两点.
（1）设l的斜率为1，求
与
夹角的大小；
（2）设
=λ
，若λ∈［4，9］，求l在y轴上截距的变化范围.
分析：本题主要考查抛物线的性质、直线与抛物线的关系以及解析几何的基本方法、思想和综合解题能力.
解：（1）C的焦点为F（1，0），直线l的斜率为1，所以l的方程为y=x－1.
将y=x－1代入方程y2=4x，并整理得
x2－6x+1=0.设A（x1，y1），B（x2，y2），则有x1+x2=6，x1x2=1.
·=（x1，y1）·（x2，y2）
=x1x2+y1y2=2x1x2－（x1+x2）+1
=－3.
=
·
=
=
.
cos〈，〉=
=－
.
所以与夹角的大小为
π－arccos.
（2）由题设=λ，得
（x2－1，y2）=λ（1－x1，－y1），
|
x2－1=λ（1－x1），
①
y2=－λy1. ②
由②得y22=λ2y12.
∵y12=4x1，y22=4x2，∴x2=λ2x1. ③
联立①③解得x2=λ.依题意有λ>0，
∴B（λ，2
）或B（λ，－2）.又F（1，0），得直线l方程为（λ－1）y=2（x－1）或（λ－1）y=－2（x－1）.
当λ∈［4，9］时，l在y轴上的截距为
或－.由=
+
，
可知在［4，9］上是递减的，
∴
≤≤，－≤－≤－.
直线l在y轴上截距的变化范围为［－，－］∪［，］.
22.有点难度哟！
（14分）（北京市东城区2004~2005学年第一学期期末教学目标检测）已知常数a>0，向量m=（0，a），n=（1，0），经过定点A（0，－a），以m+λn为方向向量的直线与经过定点B（0，a），以n+2λm为方向向量的直线相交于点P，其中λ∈R.
（1）求点P的轨迹C的方程；
（2）若a=
，过E（0，1）的直线l交曲线C于M、N两点，求
·
的取值范围.
解：（1）设P点的坐标为（x，y），则
=（x，y+a），
=（x，y－a），
又n=（1，0），m=（0，a），
故m+λn=（λ，a），n+2λm=（1，2λa）.
由题知向量与向量m+λn平行，故λ（y+a）=ax.
又向量与向量n+2λm平行，故y－a=2λax.
两方程联立消去参数λ，得点P（x，y）的轨迹方程是（y+a）（y－a）=2a2x2， 即y2－a2=2a2x2.
（2）∵a=，故点P的轨迹方程为2y2－2x2=1，
此时点E（0，1）为双曲线的焦点.
①若直线l的斜率不存在，其方程为x=0，l与双曲线交于M（0，）、N（0，－），
此时·=（－1）（－－1）=1－=.
②若直线l的斜率存在，设其方程为y=kx+1，代入2y2－2x2=1化简得2（k2－1）x2+4kx+1=0.
∵直线l与双曲线交于两点，
∴Δ=（4k）2－8（k2－1）>0且k2－1≠0.
解得k≠±1.
设两交点为M（x1，y1）、N（x2，y2），
则x1+x2=
，x1x2=
.
此时·＝（x1，y1－1）·（x2，y2－1）=（x1，kx1）·（x2，kx2）
=x1x2+k2x1x2=（k2+1）x1x2
=
=（1+
）.
当－1<k<1时，k2－1<0，故·＝（1+）≤－；
当k>1或k<－1时，k2－1>0，
故·=（1+）>.
综上所述，·的取值范围是（－∞，－）∪［，+∞）.