高考第一轮复习数学：直线、平面、简单几何体（附答案）

素质能力检测（九）

一、选择题（每小题5分，共60分）

1.（2003年北京）已知α、β是平面，m、n是直线，下列命题中不正确的是

A.若m∥n，m⊥α，则n⊥α　　　　　　　　　　　　 B.若m∥α，α∩β=n，则m∥n

C.若m⊥α，m⊥β，则α∥β　　　　　　　　　　　 D.若m⊥α，mβ，则α⊥β

解析：如图，设平面γ∥α且mγ，

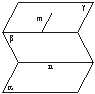
∴m∥α，但m∥n不成立（异面）.

答案：B

2.将正方形ABCD沿对角线BD折成一个120°的二面角，点C到达点C₁，这时异面直线AD与BC₁所成角的余弦值是

A. 　　　　　　　　　　B. 　　　　　　　　　　　　C. 　　　　　　　　　　D.

解析：由题意易知∠ABC₁是AD与BC₁所成的角，解△ABC₁，得余弦为.选D.

答案：D

3.一个长方体共一顶点的三个面的面积分别是、、，这个长方体对角线的长为

A.2　　　　　　　　　　　　B.3　　　　　　　　　　　　C.6　　　　　　　　　　　　　　　D.

解析：设长宽高为a、b、c，则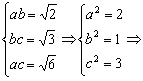l=，选D.

答案：D

4.已知l、m、n是直线，α、β是平面，下列命题中是真命题的是

A.若m∥α，n∥α，则m∥n

B.设α—l—β是直二面角，若m⊥l，则m⊥β

C.若m、n在α内的射影依次是一个点和一条直线，且m⊥n，则nα或n∥α

D.设m、n是异面直线，若m∥α，则n与α相交

解析：当m∥α，n∥α时，m、n可相交、平行、异面，α—l—β是直二面角，m⊥l，m可在β内.若m、n异面，m∥α，则nα或n∥α或n与α相交.

答案：C

5.（2003年春季北京）如图，在正三角形ABC中，D、E、F分别为各边的中点，G、H、I、J分别为AF、AD、BE、DE的中点.将△ABC沿DE、EF、DF折成三棱锥以后，GH与IJ所成角的度数为

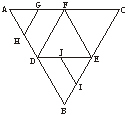
A.90°　　　　　　　　　　　　 B.60°　　　　　　　　　　　　 C.45°　　　　　　　　　　　　 D.0°

解析：平面图形折叠后为正三棱锥.如图，取EF的中点M，连结IM、MJ，则MJFD，GHFD，∴MJ∥GH，∠IJM为异面直线GH与JI所成的角.

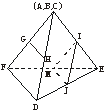
由已知条件易证△MJI为正三角形.∴∠IJM=60°.

答案：B

6.如图，点P在正方形ABCD所在的平面外，PD⊥平面ABCD，PD=AD，则PA与BD所成角的度数为

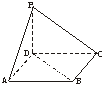
A.30°　　　　　　　　　　　　 B.45°　　　　　　　　　　　　 C.60°　　　　　　　　　　　　 D.90°

答案：C

7.正方体A′B′C′D′—ABCD的棱长为a，EF在AB上滑动，且EF=b（b＜a），Q点在D′C′上滑动，则四面体A′—EFQ的体积为

A.与E、F位置有关　　　　　　　　　　　　　　　　　　　　B.与Q位置有关

C.与E、F、Q位置都有关　　　　　　　　　　　　　　　D.与E、F、Q位置均无关，是定值

解析：V_A′－EFQ=V_Q－A′EF.

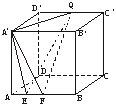
答案：D

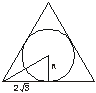
8.（理）高为5，底面边长为4 的正三棱柱形容器（下有底），可放置最大球的半径是

A. 　　　　　　　　　　　　　　　　　　　　　　　　　　　B.2

C.　　　　 　　　　　　　　　　　　　　　　　　　　　 D.

解析：过球心作平行于底的截面，

R=2tan30°=2.

答案：B

（文）（2004年全国）三个两两垂直的平面，它们的三条交线交于一点O，点P到三个平面的距离比为1∶2∶3，PO=2，则P到这三个平面的距离分别是

A.1，2，3　　　　　　　　　　B.2，4，6　　　　　　　　　　C.1，4，6　　　　　　　　　　D.3，6，9

答案：B

9.二面角α—l—β的平面角为120°，A、B∈l，ACα，BDβ，AC⊥l，BD⊥l，若AB=AC=BD=1，则CD的长为

A.　　　　　　　　　　　　　B.　　　　　　　　　　　　　C.2　　　　　　　　　　　　　　　D.

答案：B

10.在△ABC中，AB=AC=5，BC=6，PA⊥平面ABC，PA=8，则P到BC的距离为

A.　　　　　　　　　　　　　B.2　　　　　　　　　　　　 C.3　　　　　　　　　　　　D.4

解析：取BC的中点E，连结AE、PE，由AE⊥BC知PE⊥BC，即PE为点P到BC的距离.

答案：D

11.条件甲：四棱锥的所有侧面都是全等三角形，条件乙：这个四棱锥是正四棱锥，则条件甲是条件乙的

A.充分不必要条件　　　　　　　　　　　　　　　　　　　　　　　　 B.必要不充分条件

C.充要条件　　　　　　　　　　　　　　　　　　　　　　　　　　 D.既不充分也不必要条件

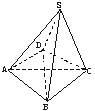
解析：乙甲，但甲乙，例如四棱锥S—ABCD的底面ABCD为菱形，但它不是正四棱锥.

答案：B

12.已知棱锥的顶点为P，P在底面上的射影为O，PO=a，现用平行于底面的平面去截这个棱锥，截面交PO于点M，并使截得的两部分侧面积相等，设OM=b，则a与b的关系是

A.b=（－1）a　　　　B.b=（+1）a　　　　　C.b= 　　　　　　 D.b=

解析：由平行锥体底面的截面性质，知=，∴=.∴= .∴b=a.故选C.

答案：C

二、填空题（每小题4分，共16分）

13.（2004年广东，15）由图（1）有面积关系：=，则由图（2）有体积关系：=_____________.

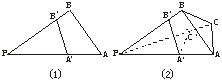
答案：

14.P、Q是半径为R的球面上两点，它们的球面距离是R，则过P、Q的平面中，与球心最大的距离是__________.

解析：以PQ为直径的圆所在的平面到球心的距离为所求.

答案：R

15.（2005年春季北京，12）如图，正方体ABCD—A₁B₁C₁D₁的棱长为a.将该正方体沿对角面BB₁D₁D切成两块，再将这两块拼接成一个不是正方体的四棱柱，那么所得四棱柱的全面积为__________.

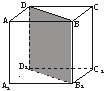
答案：（4+2）a²

16.已知异面直线a、b的公垂线段AB的长为10 cm，点A、M在直线a上，且AM=5 cm，若直线a、b所成的角为60°，则点M到直线b的距离是__________.

解析：如图，过B作BN∥a，且BN与b确定的平面为α，过M作MN⊥α于N，过N作NC⊥b于C，连结MC，由三垂线定理知，MC⊥b，故MC即为所求.在Rt△BCN中，NC=BNsin60°=，

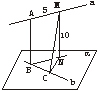
∴MC==.

答案：

三、解答题（本大题共6小题，共74分）

17.（12分）（2003年上海）已知平行六面体ABCD—A₁B₁C₁D₁中，A₁A⊥平面ABCD，AB=4，AD=2.若B₁D⊥BC，直线B₁D与平面ABCD所成的角等于30°，求平行六面体ABCD—A₁B₁C₁D₁的体积.

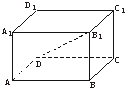
解：连结BD，

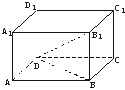
∵B₁B⊥平面ABCD，B₁D⊥BC，∴BC⊥BD.

在△BCD中，BC=2，CD=4，∴BD=2.

又∵直线B₁D与平面ABCD所成的角等于30°，

∴∠B₁DB=30°.

于是BB₁=BD=2.

故平行六面体ABCD—A₁B₁C₁D₁的体积为S_ABCD·BB₁=8.

18.（12分）（2004年广东，18）如下图，在长方体ABCD—A₁B₁C₁D₁中，已知AB=4，AD=3，AA₁=2，E、F分别是线段AB、BC上的点，且EB=FB=1.

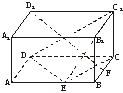
（1）求二面角C—DE—C₁的正切值；

（2）求直线EC₁与FD₁所成角的余弦值.

解：（1）以A为原点，、、分别为x轴、y轴、z轴的正向建立空间直角坐标系，则有D（0，3，0）、D₁（0，3，2）、E（3，0，0）、F（4，1，0）、C₁（4，3，2）.

于是，=（3，－3，0）， =（1，3，2）， =（－4，2，2）.

设向量n=（x，y，z）与平面C₁DE垂直，则有 n⊥　　　　　　3x－3y=0

n⊥ 　　　　 x+3y+2z=0

x=y=－z.

∴n=（－，－，z）=（－1，－1，2），其中z>0.

取n₀=（－1，－1，2），则n₀是一个与平面C₁DE垂直的向量.

∵向量=（0，0，2）与平面CDE垂直，

∴n₀与所成的角θ为二面角C—DE—C₁的平面角.

∴cosθ===.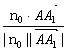

∴tanθ=.

（2）设EC₁与FD₁所成的角为β，则

cosβ===.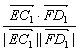

19.（12分）（2005年春季上海，19）已知正三棱锥P—ABC的体积为72，侧面与底面所成的二面角的大小为60°.

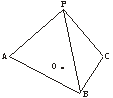
（1）证明：PA⊥BC；

（2）求底面中心O到侧面的距离.

（1）证明：取BC边的中点D，连结AD、PD，则AD⊥BC，PD⊥BC，故BC⊥平面APD.

∴PA⊥BC.

（2）解：如下图，由（1）可知平面PBC⊥平面APD，则∠PDA是侧面与底面所成二面角的平面角.

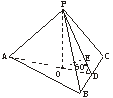
过点O作OE⊥PD，E为垂足，则OE就是点O到侧面的距离.

设OE为h，由题意可知点O在AD上，

∴∠PDO=60°，OP=2h，OD=.

∴BC=4h.

∴S=（4h）²=4h².

∵72= ·4h²·2h=h³，∴h=3，

即底面中心O到侧面的距离为3.

20.（12分）（理）如图，已知矩形ABCD，PA⊥平面ABCD，M、N分别是AB、PC的中点，设AB=a，BC=b，PA=c.

（1）建立适当的空间直角坐标系，写出A、B、M、N点的坐标，并证明MN⊥AB；

（2）平面PDC和平面ABCD所成的二面角为θ，当θ为何值时（与a、b、c无关），MN是直线AB和PC的公垂线段.

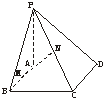
（1）证明：以A为原点，分别以AB、AD、AP为x轴、y轴、z轴，建立空间直角坐标系.

则A（0，0，0），B（a，0，0），M（，0，0），N（，，）.

=（a，0，0），=（0，，）.

·=0AB⊥MN.

（2）解：P（0，0，c），C（a，b，0），=（a，b，－c），若MN是PC、AB的公垂线段，则·=0，即－+=0b=c.

CD⊥PD，

又∵AP⊥面ABCD

CD⊥DA　　　　　　　　　　　

∴∠PDA是二面角P—CD—A的平面角.

∴∠PDA=45°，

即二面角P—CD—A是45°.

（文）正方体ABCD—A₁B₁C₁D₁中，M、N、P分别为棱AB、BC、DD₁的中点.

（1）求证：PB⊥平面MNB₁；

（2）设二面角M—B₁N—B为α，求cosα的值.

（1）证明：如图，以D为原点，DA、DC、DD₁分别为x轴、y轴、z轴建立空间直角坐标系，取正方体棱长为2，则P（0，0，1）、M（2，1，0）、B（2，2，0）、B₁（2，2，2）.

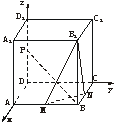
∵· =（2，2，－1）·（0，1，2）=0，

∴MB₁⊥PB，同理，知NB₁⊥PB.

∵MB₁∩NB₁=B₁，∴PB⊥平面MNB₁.

（2）∵PB⊥平面MNB₁，BA⊥平面B₁BN，∴=（2，2，－1）与=（0，2，0）所夹的角即为α，cosα==.

21.（12分）已知四棱锥P—ABCD中，PA⊥面ABCD，底面ABCD为菱形，∠BAD=60°，AB=2，PA=4，E为PC的中点.

（1）求证：平面BDE⊥平面ABCD；

（2）求二面角B—DE—C的大小.

（1）证明：设AC∩BD=O，连结OE.

∵E为PC的中点，O为AC的中点.

∴EO∥PA.

∵PA⊥面ABCD，∴EO⊥面ABCD.

∵EO平面BDE，∴面BDE⊥面ABCD.

（2）解法一：过O作OF⊥DE于F，连结CF.

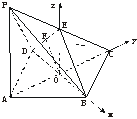
由（1）可知OC⊥面BDE，

∴DE⊥FC.

∴∠OFC为B—DE—C的平面角.

∵OE=PA=2，OD=1，∴OF=.

又∵OC=，∴tan∠OFC==.

∴二面角B—DE—C的大小为arctan.

解法二：以O为原点建立如上图所示的坐标系，则为平面EBD的法向量，=（0，，0）.

设平面CDE的法向量n=（x，y，z）.

∵E（0，0，2），C（0，，0），D（－1，0，0），

∴=（1，，0）， =（0，－，2）.

∵n·=0，n·=0，

∴

∴

　　x+y=0，　　　　　x=－y，

－y+2z=0. 　　　z=y.

取y=，则n=（－3，，）.∴cos〈n，〉==.

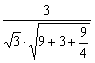∴二面角B—DE—C的大小为arccos.

22.（14分）如图，ABCD是边长为1的正方形，M、N分别是DA、BC上的点，且MN∥AB，现沿MN折成直二面角AB—MN—CD.

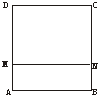
（1）求证：平面ADC⊥平面AMD；

（2）设AM=x（0<x<1），MN到平面ADC的距离为y，试用x表示y；

（3）点M在什么位置时，y有最大值，最大值为多少?

（1）证明：∵ABCD是正方形，且MN∥AB∥CD，∴MN⊥AM，MN⊥DM，即CD⊥AM，CD⊥DM，∴CD⊥平面AMD.

∵CD平面ADC，

∴平面ADC⊥平面AMD.

（2）解：∵MN∥CD，∴MN∥平面ADC.故MN到平面ADC的距离即为M到平面ADC的距离.过M作MH⊥AD于H，∵平面ADC⊥平面AMD，

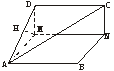
∴MH⊥平面ADC，即MH为所求距离.

在Rt△AMD中，求得y==（0<x<1）.

（3）解：y≤=≤，当且仅当x=1－x，即x=时，y_max=，此时M为AD的中点.