高考第一轮复习数学：直线和圆的方程（附答案）

素质能力检测（七）

一、选择题（每小题5分，共60分）

1.集合M={（x，y）y=，x、y∈R}，N={（x，y）x=1，y∈R}，则M∩N等于

A.{（1，0）}　　　　　　　　　　　　  B.{y0≤y≤1}

C.{1，0}　　　　　　　　　　　　　　  D.

解析：y=表示单位圆的上半圆，x=1与之有且仅有一个公共点（1，0）.

答案：A

2.（2004年湖北，文2）已知点M₁（6，2）和M₂（1，7），直线y=mx－7与线段M₁M₂的交点M分有向线段M₁M₂的比为3∶2，则m的值为

A.－　　　　　　　　　　　　　　　 B.－

C.　　　　　　　　　　　　　　　　 D.4

解析：设M（x，y），点M分M₁M₂所成比为λ=.

得x==3，y==5.

代入y=mx－7，得m=4.

答案：D

3.（2003年辽宁）在同一直角坐标系中，表示直线y=ax与y=x+a正确的是

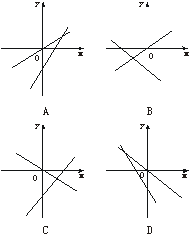
解：根据a的符号和表示直线的位置特征，显见C正确，因为当a<0时，y=ax表示过原点且下降的直线，y=x+a表示纵截距小于零且上升的直线.故选C.

答案：C

4.（2005年春季北京，6）直线x+y－2=0被圆（x－1）²+y²=1所截得的线段的长为

A.1　　　　　　　 B.　　　　　　  C.　　　　　　　 D.2

解析：圆心（1，0），r=1到直线x+y－2=0的距离d==.

则弦长=.∴弦长为.

答案：C

5.（2004年湖北，4）圆C₁：x²+y²+2x+2y－2=0与圆C₂：x²+y²－4x－2y+1=0的公切线有

A.1条　　　　　　 B.2条　　　　　　 C.3条　　　　　　  D.4条

解析：圆C₁的圆心C₁（－1，－1），r₁=2，

圆C₂的圆心C₂（2，1），r₂=2.

∵C₁C₂==<r₁+r₂=4，

∴圆C₁与圆C₂相交.故公切线有2条.

答案：B

6.（2004年天津，理7）若P（2，－1）为圆（x－1）²+y²=25的弦AB的中点，则直线AB的方程是

A.x－y－3=0　　　　　　　　　　　　  B.2x+y－3=0

C.x+y－1=0　　　　　　　　　　　　　 D.2x－y－5=0

解：由（x－1）²+y²=25知圆心为Q（1，0）.据k_QP·k_AB=－1，

∴k_AB=－=1（其中k_QP==－1）.

∴AB的方程为y=（x－2）－1=x－3，即x－y－3=0.

答案：A

（θ为参数）上，则x2+y2的最大值是

7.如果点P（x，y）在曲线

　　　　　　　　　　　　  x=3+5cosθ，

y=－4+5sinθ

A.10　　　　　　　 B.16　　　　　　　 C.25　　　　　　　 D.100

解析：易知是圆（x－3）²+（y+4）²=25上的点到原点的距离.

答案：D

8.把直线x－2y+λ=0向左平移1个单位，再向下平移2个单位后，所得直线正好与圆x²+y²+2x－4y=0相切，则实数λ的值为

A.3或13　　　　　　　　　　　　　　 B.－3或13

C.3或－13　　　　　　　　　　　　　  D.－3或－13

解析：直线x－2y+λ=0按a=（－1，－2）平移后的直线为x－2y+λ－3=0，与圆相切，易得λ=13或3.

答案：A

9.圆x²+y²+2x+4y－3=0上到直线x+y+1=0的距离为的点共有

A.1个　　　　　　 B.2个　　　　　　  C.3个　　　　　　  D.4个

解析：易知圆心（－1，－2）到x+y+1=0的距离d=，所以满足题意的点共有3个.

答案：C

10.已知曲线C：

x=1+cosθ，

y=1－sinθ　　（θ为参数），直线l经过点（0，），倾斜角为α，则α=是直线l与曲线C相切的

A.充分不必要条件

B.必要不充分条件

C.充要条件

D.既不充分也不必要条件

解析：数形结合法易知.

答案：A

11.如果直线y=kx+1与圆x²+y²+kx+my－4=0交于M、N两点，且M、N关于直线x+y=0对称，则不等式组

表示的平面区域的面积是

kx－y+1≥0，

kx－my≤0，

y≥0　　　　

A.　　　　　　　 B.　　　　　　　 C.1　　　　　　　　 D.2

解析：由题中条件知k=1，m=－1，易知区域面积为.

答案：A

12.（2002年全国新课程）平面直角坐标系中，O为坐标原点，已知两点A（3，1）、　　　　　　 B（－1，3），若点C满足=α+β，其中α、β∈R，且α+β=1，则点C的轨迹方程为

A.（x－1）²+（y－2）²=5

B.3x+2y－11=0

C.2x－y=0

D.x+2y－5=0

解析：设C点坐标为（x，y），则=（x，y），=（3，1），=（－1，3），

所以（x，y）=α·（3，1）+β·（－1，3）=（3α－β，α+3β）.

所以

　　　x=3α－β，

y=α+3β，

变形得

　　　　α=，

β=.

因为α+β=1，

所以+=1，即x+2y－5=0.故选D.

答案：D

二、填空题（每小题4分，共16分）

13.（2005年北京东城区目标检测题）设实数x、y满足

则z=x+y的最大值是____________.

x≥0，

x－y+2≤0，

2x+y－5≤0，

解析：画出图形即可得到在（0，5）点z=x+y取得最大值5.

答案：5

14.（2004年春季北京）若直线mx+ny－3=0与圆x²+y²=3没有公共点，则m、n满足的关系式为____________；以（m，n）为点P的坐标，过点P的一条直线与椭圆+=1的公共点有____________个.

解析：将直线方程代入圆方程中“Δ＜0”即可.

答案：0＜m²+n²＜3  2

15.（2004年北京，11）圆x²+（y+1）²=1的圆心坐标是__________，如果直线x+y+a=0与该圆有公共点，那么实数a的取值范围是__________.

解析：由圆的定义知，圆x²+（y+1）²=1的圆心坐标是（0，－1）.

圆心（0，－1）到直线x+y+a=0的距离d=.

若圆与直线有公共点，则d≤1，即得1－≤a≤1+.

答案：（0，－1）  1－≤a≤1+

16.（2001年上海，理）已知两个圆：①x²+y²=1；②x²+（y－3）²=1，则由①式减去②式可得两圆的对称轴方程.将上述命题在曲线仍为圆的情况下加以推广，即要求得到一个更一般的命题，而已知命题应成为所推广命题的一个特例.推广命题为____________.

解析：设两圆方程为（x－a）²+（y－b）²=r²①和（x－c）²+（y－d）²=r².②

由①－②得两圆的对称轴方程为2（c－a）x+2（d－b）y+a²+b²－c²－d²=0.

所以推广命题为：已知两个圆：①（x－a）²+（y－b）²=r²；②（x－c）²+（y－d）²=r².

则由①式减去②式可得两圆的对称轴方程.

答案：已知两个圆：①（x－a）²+（y－b）²=r²；②（x－c）²+（y－d）²=r².则由①式减去②式可得两圆的对称轴方程.

三、解答题（共6小题，满分74分）

17.（12分）已知两直线l₁：x+ysinθ－1=0和l₂：2xsinθ+y+1=0，试求θ的值，使得

（1）l₁∥l₂；（2）l₁⊥l₂.

解：（1）当sinθ=0时，l₁斜率不存在，l₂斜率为零，l₁显然不平行于l₂.

当sinθ≠0时，k₁=－，k₂=－2sinθ.

∵k₁=k₂是l₁∥l₂的条件，

∴－=－2sinθ，sinθ=±，

θ=nπ+，n∈Z.此时两直线截距不等，

∴当θ=nπ±，n∈Z时，l₁∥l₂.

（2）∵A₁A₂+B₁B₂=0是l₁⊥l₂的充要条件，∴2sinθ+sinθ=0.

∴sinθ=0，即θ=nπ（n∈Z）.

∴当θ=nπ，n∈Z时，l₁⊥l₂.

18.（12分）过点P（2，4）作两条互相垂直的直线l₁、l₂，若l₁交x轴于A点，l₂交y轴于B点，求线段AB的中点M的轨迹方程.

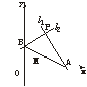
解法一：设点M的坐标为（x，y），

∵M为线段AB的中点，

∴A的坐标为（2x，0），B的坐标为（0，2y）.

∵l₁⊥l₂，且l₁、l₂过点P（2，4），

∴PA⊥PB，k_PA·k_PB=－1.

而k_PA=，k_PB=（x≠1），

∴·=－1（x≠1）.

整理，得x+2y－5=0（x≠1）.

∵当x=1时，A、B的坐标分别为（2，0）、（0，4），

∴线段AB的中点坐标是（1，2），它满足方程x+2y－5=0.

综上所述，点M的轨迹方程是x+2y－5=0.

解法二：设M的坐标为（x，y），则A、B两点的坐标分别是（2x，0）、（0，2y），连结PM，∵l₁⊥l₂，

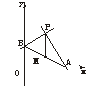
∴2｜PM｜=｜AB｜.

而｜PM｜=，｜AB｜=，

∴2=.化简，得x+2y－5=0，为所求轨迹方程.

解法三：设M的坐标为（x，y），由l₁⊥l₂，BO⊥OA知O、A、P、B四点共圆，

∴｜MO｜=｜MP｜，即点M是线段OP的垂直平分线上的点.

∵k_OP==2，线段OP的中点为（1，2），

∴y－2=－（x－1），即x+2y－5=0为所求.

19.（12分）圆C通过不同的三点P（k，0）、Q（2，0）、R（0，1），已知圆C在P点切线斜率为1，试求圆C的方程.

解：设圆C的方程为x²+y²+Dx+Ey+F=0.

将P、Q、R的坐标代入，得

　　　　　　　　　　　　　  k+2=－D，

2k=F，

E+F+1=0.

∴圆的方程为x²+y²－（k+2）x－（2k+1）y+2k=0，圆心为（，）.

又∵k_CP=－1，∴k=－3.

∴圆的方程为x²+y²+x+5y－6=0.

20.（12分）某房产开发公司建楼急需资金1200万元，必须向银行A和银行B贷款，一年本自息还清，银行A至多贷给该公司800万元，年息12%；银行B至多贷款给该公司1000万元，年息14%，问开发公司分别向A、B两银行贷款多少万元，才使所付总利息最少?

解：设开发公司向银行A贷款x万元，向银行B贷款y万元，开发公司需付总利息为S，依题意，有约束条件

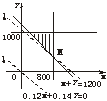
x≤800，

S=0.12x+0.14y.

y≤1000，

x+y≥1200，

x≥0，

y≥0.   

作出以上不等式组所表示的平面区域，即可行域.作直线l₀：0.12x+0.14y=0，把直线l₀向右上方平移至l₁的位置时，直线经过可行域上的点M，且与原点距离最小，此时，S=0.12x+0.14y取得最小值.

得M点的坐标为（800，400），此即为最优解.

解方程组

　　　　　  x=800，

x+y=1200，　　　　

故该开发公司向银行A贷款800万元，向银行B贷款400万元时，所付总利息最少.

21.（12分）已知圆x²+y²－6x－8y+21=0和直线kx－y－4k+3=0.

（1）求证：不论k取什么值，直线和圆总有两个不同的公共点；

（2）求当k取何值时，直线被圆截得的弦最短，并求这最短弦的长.

（1）证明：已知圆的方程为（x－3）²+（y－4）²=4，其圆心（3，4）到直线kx－y－4k+3=0的距离为=.

要证明直线和圆总有两个不同的公共点，只要证<2，即证（k+1）²<4（1+k²），

即证3k²－2k+3>0.

而3k²－2k+3=3（k－）²+>0成立.

（2）解：由于当圆心到直线的距离最大时，直线被圆截得的弦最短，

而d===≤=.

当且仅当k=1时，“=”成立，即k=1时，d_max=.

故当k=1时，直线被圆截得的弦最短，该最短弦的长为2=2.

22.（14分）过点A（0，a）作直线与圆E：（x－2）²+y²=1交于B、C两点，在BC上取满足BP∶PC=AB∶AC的点P.

（1）求P点的轨迹方程；

（2）设所求轨迹方程与圆E交于M、N两点，求△EMN（E为圆心）面积的最大值.

解：（1）设AB方程为y=kx+a，与圆的方程联立得（k²+1）x²+（2ak－4）x+a²+3=0.

x_B+x_C=－，x_B·x_C=.

∵=，∴=.

∴x_P=.

同理，y_P=.

消去k，得2x－ay－3=0.

∴轨迹是直线2x－ay－3=0在圆内一段.

（a2+4）y2－2ay+3=0.

（2）由

　　　　 2x－ay－3=0

（x－2）²+y²=1　　　　 

MN=y₁－y₂=2·.

又高为，∴S_△EMN==≤.

仅当a=0时，（S_△EMN）_max=.