哈师大附中　东北师大附中　辽宁省附中

2006年高三第二次联合模拟试卷

翱翔高考网 www.gao-kao.com

数学试卷（理科）

本试卷分选择题和非选择题两部分．共22小题．共150分．共4页。考试结束后。将本试卷和答题卡一并交回

注意事项：1.答题前．考生先将自己的姓名、准考证号码填写清楚．将条形码准确粘贴在条形码区域内。

2.选择题必须使用2B铅笔填涂；非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。

3.请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。

4.作图可先使用铅笔画出，确定后必须用照色字迹的签字笔描黑。

5.保持卡面清洁,不要折叠、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。

选  择　题

选择题共12小题，每小题5分，共60分。在每小题给出的四个选项中．只有一项是符合题目要求的。

一、选择题

1.已知集合A＝｜x｜2x+1>3,B=xx²+x-6≤0｜则A∩B＝

A.[-3,-2]∪(1,2)　　　　　　　　　　　　　　　　　　B.(-3,-2)∪（1+∞）

C.(-3,-2] [1,2]　　　　　　　　　　　　　　　　　　　 D.(-∞,-3)∪(1,2]

2.若，则a的值是

　A.2　　　　　　　　　　　　　 B.-2　　　　　　　　　　　C.6　　　　　　　　　　　 D.-6

3.命题P：函数f(x)=sin(2x-)+1满足f()=f()

命题q：函数g(x)=sin(2x+θ)+1可能是奇函数（θ为常数）；则复合命题“p或q”“p且q”“非q”为真命题的个数为

A.0个　　　　　　　　　　　B.1个　　　　　　　　　 C.2个　　　　　　　　　 D.3个

4.在公差为2的等差数列{a_n}中，如果前17项和为S₁₇=34,那么a₁₂的值为

　A.2　　　　　　　　　　　　　 B.4　　　　　　　　　　　 C.6　　　　　　　　　　　 D.8

5.曲线y²sinx+2y-1=0先向左平移π个单位，再向下平移1个单位，得到的曲线方程是

　A.（y-1）²sinx-2y+3=0　　　　　　　　　　　　　B.(y-1)²sinx+2y-3=0

  C.(y+1)²sinx-2y-1=0　　　　　　　　　　　　　　　 D.(y+1)²sinx+2y+1=0

6.函数y=()^x与函数y=-的图象关于

A.直线x=2对称　　　　　　　　　　　　　　　　　　B.点（4，0）对称

C.直线x=4对称　　　　　　　　　　　　　　　　　　D.点（2，0）对称

7.已知函数f(x)=x·sinx,若A、B是锐角三角形两个内角，则

　A.f(-sinA)>f(-sinB)　　　　　　　　　　　　　　　　B.f(cosA)>f(cosB)

  C.f(-cosA)>f(-sinB)　　　　　　　　　　　　　　　 D.f(cosA)<f(sinB)

8.若直线y=与双曲线=1(a>0,b>0)的交点在实轴上的射影恰好为双曲线的焦点，则双曲线的离心率为

 A.　　　　　　　　　　　　B.2　　　　　　　　　　　　　　　C.2　　　　　　　　　　　　D.4

9.三棱锥A-BCD中：△ABC和△DBC是全等的正三角形，边长为2，且AD=1，则三棱锥A-BCD的体积为

 A.　　　　　　　　　　　 B.　　　　　　　　　　　　 C.　　　　　　　　　　　　 D.

10.口袋里放有大小相等的两个红球和一个白球，有放回地每次摸取一个球，定义数列{a_n}；

　a_n=，如果S_n为数列{a_n}的前n项和，那么S₇=3的概率为

 A.C　　　　 B. C　　　　　　　C. C　　　　　D. C

11.将正方体ABCD-A₁B₁C₁D₁的各面涂色，任何相邻两不同色，现在有5个不同的颜色，并且涂好了过顶点A的3个面的颜色，那么其余3个面的涂色方案共有

 A.15种　　　　　　　　　　　B.14种　　　　　　　　　　　　C.13种　　　　　　　　　　　　D.12种

12.已知函数f(x)=x³+bx²+cx+d在区间[-1，2]上是减函数，那么b+c

 A.有最大值　　　　　 B.有最大值-　　　　　　C.有最小值　　　　　　 D.有最小值-

非 选 择 题tx

(非选择题共10小题，共90分)

二、填空题：本大题共4小题每小题4分，t共16分。

13.在(1-x³)(1+x)¹⁰的展开式中，x⁵的系数为____________.

14.已知向量，直线l过点A(3，-1)且与向量垂直，则直线l的方程为___________

15.f(x)是定义在(0，+∞)上的增函数，对正实数x,y都有：f(xy)=f(x)+f(y)成立，则不等式f(log₂x)<0的解集为_________

16.将正方形ABCD沿对角线BD折成直二面角A-BD-C，有如下四个结论：

　①AC⊥BD　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ②△ACD是等边三角形

③AB与平面BCD成60°的角　　　　　　　　　　　　　　④AB与CD所成的角为60°

其中真命题的编号是____________(写出所有真命题的编号)

三、解答题：x

17.(本题满分12分)在△ABC中，角A、B、C所对的边是a,b,c，且a²+c²-b²=

  (1)求sin²+cos2B的值

  (2)若b=2,求△ABC面积的最大值.

18.(本题满分12分)旅游公司为3个旅游团提供4条旅游线路，每个旅游团任选其中一条.

  (1)求3个旅游团选择3条不同的线路的概率

  (2)求恰有2条线路没有被选择的概率.

  (3)求选择甲线路旅游团数的期望.

19.如图：四棱锥P-ABCD底面为一直角梯形，AB⊥AD、CD⊥AD、CD=2AB，PA⊥面ABCD、E为PC中点.

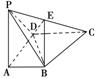　　　　　　　　　　　　　 (1)求证：平面PDC⊥平面PAD

　　　　　　　　　　　　　 (2)求证：BE∥平面PAD

　　　　　　　　　　　　　 (3)假定PA=AD=CD，求二面有E-BD-C的平面角的正切值.

20.(本题满分12分)设数列a_n和b_n满足：a₁=b₁=6,a₂=b₂=4,a₃=b₃=3,且数列a_n+1-a_n(n∈N*)是等差数列，数列b_n-2(n∈N*) 是等比数列.

　(1)求数列a_n和b_n的通项公式.

　(2)是否存在k∈N*,使a_k-b_k∈(0,)?若存在，求出k,若不存在，说明现由.

21.(本题满分14分)双曲线C的渐近线方程为x±2y=0,点A(5，0)到双曲线C上动点P的距离的小值为.

　(1)求双曲线方程.

　(2)若过B(1，0)点的直线l交双曲线C上支一点M，下支一点N，且4,求直线l的方程.

22.(本题满分12分)设函数f(x)=在[1+,∞）上为增函数.

　(1)求正实数a的取值范围.

(2)若a=1,求征： (n∈N*且n≥2)

2006年东北三省三校高三第二次联合考试

tx理科数学试题标准答案及评分标准

一、选择题

1	2	3	4	5	6	7	8	9	10	11	12
A	D	C	D	C	D	D	B	B	B	C	B

二、填空题：

13.207　　　　14.2x-3y-9=0　　　　 15.(1,2)　　　　　16.①②④

三、解答题：

17.解：(1)∴a²+c²-b²=

　　　 ∴cosB=

　　　 ∴sin²[1-cos(A+C)]+[2cos²B-1]

　　　　　　　　　　　　　　　　　 　=[1+cosB]+[2cos²B-1]　

　　　　　　　　　　　　　　　　　=[1+]+[2×]

　　　　　　　　　　　　　　　　　=-　　

(2)由cosB=得：sinB=　∵b=2

∴a²+c²=ac+4≥2ac(当且仅当a²=c²=时取“=”号)

∴ac≤　 ∴S_△ABC=ac·sinB≤××=

故：△ABC面积的最大值为

18.解：(1)3个旅游团选择3条不同线路的概率为：

　　　　　　　P₁=

　　　 　 (2)恰有两条线路没有被选择的概率为：

　　　　　　　P₂=

　　　 　 (3)设选择甲线路旅游团数为ξ，则ξ=0，1，2，3

　　　　　　　P(ξ=0)=

　　　　　　　P(ξ=1)=

　　　　　　　P(ξ=2)=

　　　　　　　P(ξ=3)=

 ∴ξ的分布列为：

ξ	1	2	3	4
P

　　　

 ∴期望Eξ=0×+1×+2×+3×=　

19.(1)证明：∵PA⊥面ABCD

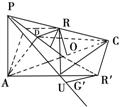　　　　　　　　　　　　　　　　　 ∴PA⊥DC

　　　　　　　　　　　　　　　　　 ∵DC⊥AD且AD∩PA=A

　　　　　　　　　　　　　　　　　 ∴DC⊥面PAD

　　　　　　　　　　　　　　　　　 ∵DC面PDC

　　　　　　　　　　　　　　　　　 ∴平面PDC⊥平面PAD

(2)证明：取PD中点F，连接EF，FA。

∴E为PC中点，∴在△PDC中：EFDC∴EFAB

∴四边形ABEF为平行四边形，即：BE∥AF

∵AF面PAD且BE面PAD

∴BE∥平面PAD

(3)解：连接AC，取AC中点O，连接EO。

在△PAC中：EO PA

∴EO⊥面ABC

过O作OG⊥BD交BD于G，连接EG。

由三垂线定理知:∠EGO为所求二面角E-ED-C的平面角

设PA=AD=CD=2a，AB=a，∴EO=a

连DO并延长交AB于B′，则四边形AB′CD为正方形，且B′B=a，O为DB′中点，过B′作B′G′⊥DB交BD于G′.

∴OG=B′G′=BB′sin∠B′BG′=BB′·sin∠ABD

　　　=a·

在△EOG中：tan∠EGO=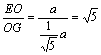

故：二面角E-BD-C的平面角的正切值为 

20.解：(1)由已知a₂-a₁=-2,a₃-a₂=-1,d=-1-(-2)=1

　∴a_n+1-a_n=(a₂-a₁)+(n-1)×1=n-3　　　

　∴a_n=a₁+(a₂-a₁)+(a₃-a₂)+…+(a_n-a_n-1)

　=6+(-2)+(-1)+0+01+2+…+(n-4)

= 

由已知：b₁-2=4,b₂-2=2,即：q=

∴b_n-2=(b₁-2)·()^a-1=4·()^n-1=8·()ⁿ

∴b_n=2+8·()^a

(2)设f(k)=a_k-b_k=k²-k-8·()^k+7

当k≥4时：k²-是k的增函数；-8·()^k也是k的增函数.

∵f(4)=　 ∴k≥4时；f(k)≥　

又∵f(1)=f(2)=f(3)=0 　∴不存在k，使f(k)∈(0, )　　　

21.解：(1)若双曲线焦点在x轴上，∵渐近线方程为y=±x

  ∴双曲线方程设为 

  设动点P的坐标为(x、y)，则AP=

  ∵x∈(-∞,-2b)∪[2b,+∞]

  ∴①若x=4≤2b，即b≥2,则当x=2b时，APmin=

解得：b=

此时双曲线方程为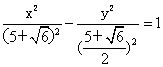

②若x=4>2b,即：b<2，则当x=4时：APmin==

∴b²=-1，无解　 …5分

  若双曲线焦点在y轴上，双曲线方程可设为(b>0)

  ∴PA=

  ∵x∈R∴x=4时：PAmin==∴b=1

  此时双曲线方程为： y²-=1

  综上所求：

  双曲线方程为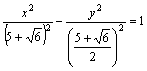或y²-=1

(2)由(1)知：双曲线方程为y²-=1,设直线l方程为x=ky+1

由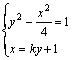得：(4-k²)y²-2ky-5=0

依题意：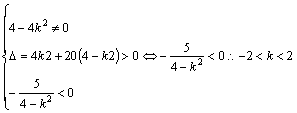 

设M(x₁、y₁),y­_­1>0,N(x₂,y₂),y₂<0

由韦达定理得：y₁+y₂=①;y₁·y₂=-②

∵4M∴-4y₁=5y₂③

由③得：y₁=-代入①②得：-④

-⑤

由④⑤消去y₂解得：k=　∴直线L的方程为：x=y+1

22.(1)由已知：f′(x)= 

　 依题意得：≥0对x∈[1，+∞]恒成立

　 ∴ax-1≥0对x∈[1,+∞]恒成立　  ∴a-1≥0即：a≥1　　

　 (2)∵a=1　 ∴由(1)知：f(x)=在[1,+∞)上为增函数，

　 ∴n≥2时：f()=

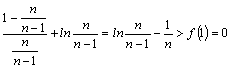
　 　即：　　∴

设g(x)=lnx-x　x∈[1,+∞),则g′(x)在[1+∞)为减函数

∴n≥2时：g()=ln-<g(1)=-1<0

即：ln<=1+(n≥2)

∴ln

综上所证：(n∈N*且≥2)成立.