风化店中学第一学期高三数学期中试卷
注意：看清文理试题
|
1．设全集为实数集R，M={
，N=
，则（ RM）∩N=（ b ）
A．{
B．{
}
C．{
} D．{
}
2．设集合P={1，2，3}，Q={0，1，3，4}. 
，满足上述条件的非空集合M共有 （ a
）
A．3个 B．4个 C．8个 D．16个
3．设P：
，则P是q的 （ b ）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
4．若命题“p且q”与命题“p或q”都是假命题，则下列判断正确的是 （ d ）
A．命题“非p”与“非q”真假不同
B．命题“非p”与“非q”中至少有一个是假命题
C．命题“非p”与q的真假相同
D．命题“非p且非q”是真命题
5．定义两种运算：
，
，则函数
为（ ）
（A）奇函数 （B）偶函数
（C）奇函数且为偶函数 （D）非奇函数且非偶函数
6．已知函数
为奇函数，且当
时，
，则当
时的递增区间为 （ a ）
A．（－∞，－1） B．（－1，0） C．（－∞，0） D． 
7．如果函数
在区间（
上为增函数，则
的取值范围是（ b ）
A．
B．[－1，0] C．
D．（－1，0）
8设函数
的值是 （ c
）
A．
B．
C．
D．2
9．等差数列
的前
项和为
，若
（a ）
A．36 B．18 C．72 D．9
10．（文）在等差数列{
}中，
=45，
= （ c ）
A．22 B．20 C．13 D．18
（理）设函数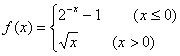
，若
则
的取值范围是 （ c
）
A．（－1，1） B．（－1，+∞）
C．（－∞，－1）∪（1，+∞） D．（－∞，－2）∪（0，+∞）
11、若数列
是等差数列，首项
，则使前n项和
成立的最大自然数n是：（ b ）
A 4005 B 4006 C 4007 D 4008
１２、（文）数列{}的通项公式
，其前n项和为10，则项数n为（ c ）
A．11 B．99 C．120 D．121
（理）
其中
为的前n项和， a、b是非零常数，则存在数列{
}、{
}使得（ c ）
A．
为等差数列，{}为等比数列
B．和{}都为等差数列
Ｃ．
为等差数列，{}都为等比数列
D．和{}都为等比数列
二、填空题：（每小题4分，共16分）
13．已知二次函数满足
如果在区间
[0，m]上最小值为1，最大值为3，则m的取值范围是 
14、定义“等和数列”：在一个数列中，如果每一项与它的后一项的和都为同一个常数，那么这个数列叫做等和数列，这个常数叫做该数列的公和。已知数列
是等和数列，且
，公和为5，那么
（文）
的值为___。
（理）这个数列的前18,19项和
的值为了
15．．已知数列{an}的前n项的和
，则数列{an}的通项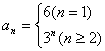
16．给出如下命题：
（1）如果为奇函数，则其图象必过（0，0）点；
（2）与
的图象若相交，则交点必在直线
上；
（3）若对定义域内任意实数
恒有
，则必为奇函数；
（4）函数=
的极小值为2，极大值为－2.
其中真命题的序号为 .（1）（2）（3）
三、解答题：（共6个小题，解答需写出必要的文字说明. 证明过程或推演步骤）
１７、设
是一个公差为
的等差数列，它的前10项和
且
，
，
成等比数列。（1）证明
；（2）求公差
的值和数列的通项公式
证明：因，，成等比数列，故
，而是等差数列，有
，
于是 
，即
，
化简得
（2）解：由条件和
，得到
，由（1），，代入上式得
，故 
，
，
１８、 （文）设f(x)=lg
,a
R, nN且n
2.若f(x)当x(-
,1)有意义，求a的取值范围．
解: f(x)当x(-,1)有意义，当且仅当1＋2
＋…＋(n-1)＋an>0 对x(-,1)恒成立．即函数
g(x)=
＋
＋…＋
＋a>0
对于任意的x(-,1)恒成立．因为g(x)在(-,1)上是减函数，
最小值为g(1)=
＋
＋…＋
＋a=
(n－1)＋a，
所以g(x)
>0对x(-,1)恒成立的充要条件是
＋a>0，即a>
．
故所求实数a的范围为（，+）
１９、（文）已知等比数列{}的公比为q，前n项和为Sn，是否存在常数c，使数列{
}也成等比数列？若存在，求出c的值；若不存在，说明理由.
解：（1）当q=1时，不存在常数c，使数列{Sn+c}成等比数列；
（2）当q≠1时，存在常数c=
，使数列{Sn+c}成等比数列.
（理）、已知数列的前n项和为
（Ⅰ）求
；（Ⅱ）求证数列是等比数列
解: (Ⅰ)由
,得
，∴
，又
,即
,得
.(Ⅱ)当n>1时,
得
所以是首项,公比为的等比数列
２０、已知函数
（1）当
时，求的最小值；
（2）若对任意
，
恒成立，求实数的取值范围.
解：（1）
利用定义或导数证明函数的单调性，直接求给与3分
方法解：（1）当时. 
任取
…………2′
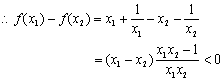
上是增函数…………4′
的最小值为………………6′
（2）依题得
对任意恒成立………………8′
设
则
故由二次函数性质可知：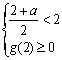
即 
………………10′
解得
故的取值范围是
………………12′
解法2：依题可得方程
其判别式
设方程两根为
则
解得 ∴的取值范围是
２１、假设你正在某公司打工，根据表现，老板给你两个加薪的方案：
（Ⅰ）每年年末加1000元； （Ⅱ）每半年结束时加300元。请你选择。
（1）如果在该公司干10年，问两种方案各加薪多少元？
（2）对于你而言，你会选择其中的哪一种？
解：设方案一第n年年末加薪an，因为每年末加薪1000元，则an=1000n；
设方案二第n个半年加薪bn，因为每半年加薪300元，则bn=300n；
(1)在该公司干10年(20个半年)，方案1共加薪S10=a1＋a2＋……＋a10=55000元。
方案2共加薪T20=b1＋b2＋……＋b20=20×300＋
=63000元；……6分
(2)设在该公司干n年，两种方案共加薪分别为：
Sn=a1＋a2＋……＋an=1000×n＋
=500n2＋500n
T2n=b1＋b2＋……＋b2n=2n×300＋
=600n2＋300n …………10分
令T2n≥Sn即：600n2＋300n>500n2＋500n，解得：n≥2，当n=2时等号成立。
∴如果干3年以上(包括3年)应选择第二方案；如果只干2年，随便选；如果只干1年，当然选择第一方案。
22．（本题满分14分）
(文)已知函数对任意实数恒有
（1）判断的奇偶性；
（2）求在区间[－3,3]上的最大值；
（3）解关于
的不等式
解（1）取
则
………………1
取
对任意
恒成立 ∴为奇函数. ………………3′
（2）任取
， 则
………………4′
又为奇函数 
∴在（－∞，+∞）上是减函数.
对任意
，恒有
………………6′
而
∴在[－3，3]上的最大值为6………………8′
（3）∵为奇函数，∴整理原式得 
进一步可得
而在（－∞，+∞）上是减函数，
………………10′
当
时，
当
时，
………………12′
当
时，
当
时
………………
（理）（本小题满分14分）已知数列
中，
且点
在直线
上.
（1）求数列
的通项公式；
（2）若函数
求函数
的最小值；
（3）设
表示数列
的前项和。试问：是否存在关于的整式
，使得
对于一切不小于2的自然数恒成立？若
存在，写出的解析式，并加以证明；若不存在，试说明理由。
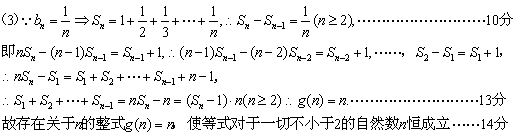
参考答案（理科）
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | C | D | C | A | B | C | D | D | A | D | C |
二、填空题
13．2003 14．1320 15．2.5 16．
三、解答题
设
是实数集R上的奇函数.
（1）确定值，并求出的反函数；
（2）对任意给定的
，解不等式
北京文理（14）
湖北卷理8文9．
数列{an}的前n项和记为Sn，已知a1＝1，an＋1＝
Sn（n＝1，2，3，…）
证明：(Ⅰ)数列{
}是等比数列；(Ⅱ)Sn＋1＝4an
证（I）由a1=1,an+1=
Sn(n=1,2,3，…)，知a2=
S1=3a1,
, 
,∴
又an+1=Sn+1-Sn(n=1,2,3，…),则Sn+1-Sn=Sn(n=1,2,3，…)，∴nSn+1=2(n+1)Sn,
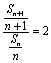(n=1,2,3，…).故数列{
}是首项为1，公比为2的等比数列
证（II） 由（I）知，
，于是Sn+1=4(n+1)·
=4an(n
)
又a2=3S1=3,则S2=a1+a2=4=4a1,因此对于任意正整数n≥1都有Sn+1=4an
全国卷二文（17）已知等差数列{an}，a2＝9，a5 ＝21
(Ⅰ)求{an}的通项公式；(Ⅱ)令bn＝
，求数列{bn}的前n项和Sn
解：a5-a2=3d,d=4,an=a2+(n-2)d=9+4(n-2)=4n+1；{bn}是首项为32公比为16的等比数列，Sn=
.
重庆卷理9．
已知数列{an}是首项为a且公比q不等于1的等比数列，Sn是其前n项的和，a1,2a7,3a4
成等差数列.（I）证明 12S3,S6,S12-S6成等比数列；（II）求和Tn=a1+2a4+3a7+…+na3n
（Ⅰ）证明 由
成等差数列， 得
，即 
变形得 
所以
（舍去）.由 
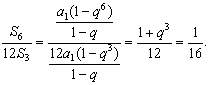
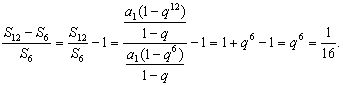得 
所以12S3，S6，S12－S6成等比数列
（Ⅱ）解：
即 
①
①×
得： 
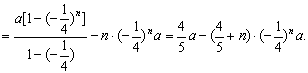所以 
已知数列，那么“对任意的
，点
都在直线
上”是“为等差数列”的A. 必要而不充分条件B. 充分而不必要条件C. 充要条件D. 既不充分也不必要条件
天津卷文20.
|
|
，则 p是 q的 （ a ）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
8．在等差数列{}中，=45，= （ d ）
A．22 B．20 C．18 D．13
12．设奇函数在[－1，1]上是增函数，且
，若函数
对所有的
都成立，当
时，则t的取值范围是 （ c
）
A．
B．
C．
D．
４．
７
８．已知
定义域为
，且对任意的
、
，恒有
，
时，
．
（１）求
的值，并证明
；
（２）求证：在
的定义域内恒有
例２．
设数列的前n项和为Sn，若
是首项为S1各项均为正数且公比为q的等比数列.
（１）求数列的通项公式（用S1和q表示）；
（２）试比较
的大小，并证明你的结论.
讲解 （１）∵是各项均为正数的等比数列，
∴
．
当n=1时，a1=S1；
当
．
∴
（２）当n=1时，
∴
．
∵
①当q=1时，
②当
③当
综上以上，我们可知：当n=1时，
．当
若
若
某地为了防止水土流失，植树造林，绿化荒沙地，每年比上一年多植相同亩数的林木，但由于自然环境和人为因素的影响，每年都有相同亩数的土地沙化，具体情况为下表所示：
| 1998年 | 1999年 | 2000年 | |
| 新植亩数 | 1000 | 1400 | 1800 |
| 沙地亩数 | 25200 | 24000 | 22400 |
而一旦植完，则不会被沙化.
问：（1）每年沙化的亩数为多少？
（2）到那一年可绿化完全部荒沙地？
．（1）由表知，每年比上一年多造林400亩.
因为1999年新植1400亩，故当年沙地应降为
亩，但当年实际沙地面积为24000亩，所以1999年沙化土地为200亩.
同理2000年沙化土地为200亩.
所以每年沙化的土地面积为200亩.
（2）由(1)知，每年林木的“有效面积”应比实造面积少200亩.
设2000年及其以后各年的造林亩数分别为
、
、
、…，则n年造林面积总和为：
.
由题意：
化简得
,
解得： 
.
故8年，即到2007年可绿化完全部沙地.
（本小题满分12分）
22在等比数列{an}中，前n项和为Sn，若Sm，Sm+2，Sm+1成等差数列，则am, am+2, am+1成等差数列.
（１）写出这个命题的逆命题；
（２）判断逆命题是否为真，并给出证明.
讲解 （１）逆命题：在等比数列{an}中，前n项和为Sn，若am, am+2, am+1成等差数列，则 Sm，Sm+2，Sm+1成等差数列.
（２）设{an}的首项为a1，公比为q
由已知得2am+2= am
+ am+1
∴2a1qm+1=a1
+a1qm
∵a1≠0 q≠0 ,
∴2q2－q－1=0 ,
∴q=1或q=－.
当q=1时，
∵Sm=ma1， Sm+2= (m+2)a1，Sm+1= (m+1)a1，
∴Sm+Sm+1≠2 Sm+2,
∴Sm，Sm+2，Sm+1不成等差数列.
当q=－时,
2 Sm+2=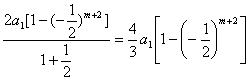
,
∴Sm+Sm+1=2 Sm+2 ,
∴Sm，Sm+2，Sm+1成等差数列．
综上得：当公比q=1时，逆命题为假；
当公比q≠1时，逆命题为真
．