福州华侨中学高三数学第二次诊断性测试
班级___________ 姓名__________ 座号__________
一、选择题：（
，请将答案填在题后的表格内）
1.已知集合A={x
}，则集合A的真子集个数为( ）
A.1个 B.2个 C.3个 D.4个
2.
，
，
是
成立的（ ）
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
3.已知函数
的反函数为
，则
的解集为（ ）
A.
B.
C.
D.
4.（理）定义在R上的函数f（x）对任意的实数x满足f (x+1)＝－f (x－1)，则下列结论一定成立的是（ ）
A. f (x)是以4为周期的周期函数 B. f (x)是以6为周期的周期函数
C. f (x)的图象关于直线x＝1对称 D. f (x)的图象关于点（1,0）对称
(文）已知正项等比数列{
}中，
,则数列{}的公比为（ ）
A.
B.2 C.±2 D.
±
5.某交往式计算机有20个终端，这些终端由各个单位独立操作，使用率均为0.8，则20个终端中至少有两个没有使用的概率为（ ）
A.
B.
C.
D.
6.点P在平面上作匀速直线运动，速度向量v =（4，－3）（即点P的运动方向与v相同，且每秒移动的距离为v个单位.设开始时点P的坐标为（－10，10），则5秒后点P的坐标为( )
A．（－2，4） B．（－30，25） C．（10，－5） D．（5，－10）
7.已知P为抛物线y2=4x上任一动点，记点P到y轴的距离为d，对于给定点A(4,5)，则PA+d的最小值为（ ）
A.4 B.
C.
D.
8.已知：
，则实数a的取值范围是（ ）
A．
B．
C．
D．
9.已知x，y满足不等式组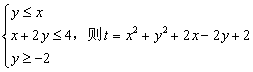
的最小值为（ ）
A. 
B. 2 C. 3
D.
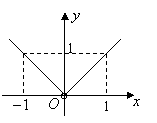
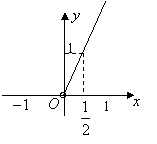
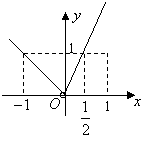10.若动点
的横坐标为
、纵坐标为
使
成等差数列，则点的轨迹图形是（ ）
A. B. C. D.
11.某校高三8个班级的师生为庆祝第二十一个教师节，每个班学生准备了一个节目，已排成节目单。开演前又增加了3个教师节目，其中2个独唱节目，1个朗诵节目，如果将这3个节目插入原节目单中，要求教师的节目不排在第一个和最后一个，并且2个独唱节目不连续演出，那么不同的插法有（ ）
A.294种 B.308种 C.378种 D.392种
12.若一系列函数的解析式相同，值域相同，但定义域不同，则称这些函数为“孪生函数”，那么函数解析式为y=2x2+1，值域为{5,19}的“孪生函数”共有（ ）
A.10个 B.9个 C.8个 D.7个
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
|
|
二、填空题（
）：
13．(x2-
展开式中各项系数之和为
.
14．（理）若等差数列
各项均为正，且
，则S12=
.
（文）函数
的周期与函数
的周期相等，则
等于 .
15．双曲线3x2-4y2-12x+8y-4=0按向量
平移后的双曲线方程为
，则平移向量=
.
16．椭圆
的半焦距为c，直线
与椭圆的一个交点横坐标为c，则该椭圆离心率为
.
三、解答题：
17．（本小题满分12分）已知函数
，求f(x)的定义域，判断它的奇偶性，并求其值域。
18．（本题12分）甲、乙两人在罚球线投球命中概率分别为
和
（1）甲、乙两人在罚球线各投球一次，求恰好命中一次的概率；
（2）甲、乙两人在罚球线各投两次，求这四次投球中至少命中一次的概率。
19．（本小题满分14分）已知△ABC的面积S满足
, 且
, 
与
的夹角为
.
(I) 求的取值范围；
(II)求函数
的最小值.
20．（本题12分）已知函数
的图像经过点
（1）求函数
的反函数；
（2）设
，求数列
的前n项和Sn.
21．（本小题满分12 分）某自来水厂的蓄水池存有400吨水，水厂每小时可向蓄水池中注水60吨，同时蓄水池又向居民小区不间断供水，
小时内供水总量为
吨，（
）
（Ⅰ）从供水开始到第几小时，蓄水池中的存水量最少？最少水量是多少吨?
（Ⅱ）若蓄水池中水量少于80吨时，就会出现供水紧张现象，请问：在一天的24小时内，有几小时出现供水紧张现象。
22．（本题满分14分）圆锥曲线C的一个焦点为F（2，0），相应的准线是直线
，以过焦点F并与
轴垂直的弦为直径的圆截准线所得弦长为2。
（Ⅰ）求圆锥曲线C的方程；
（Ⅱ）当过焦点F的直线
的倾斜角
在何范围内取值时，圆锥曲线C上有且只有两个不同的点关于直线对称？
福州华侨中学高三数学第二次诊断性测试参考答案
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | A | B | A | C | C | D | C | B | C | D | B |
一、 选择题：
二、填空题：13．1024或210；14.（理）48 ,（文）
; 15. (-2，-1);16. 
三、解答题：17．解：由
.
所以
的定义域为
因为的定义域关于原点对称，且
是偶函数.
又当
，
所以的值域为
18．解（1）记“甲投一次命中”为事件A，“乙投一次命中”为事件B，则
（2）甲、乙各投两次均不命中的概率
19．解:(Ⅰ)由题意知,
, ①
,②…………………(2分)
由②÷①, 得
, 即
由
得
, 即
.……………(4分)
又
为
与
的夹角, ∴
, ∴
.……………(6分)
(Ⅱ)
……………(10分)
∵, ∴
.……………(12分)
∴
, 即
时, 
的最小值为3. ……………(14分)
20．解（1）由已知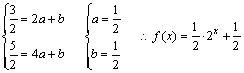
（2）
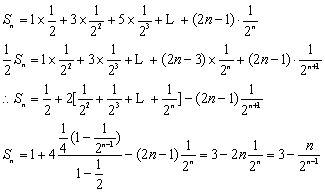
21．解：Ⅰ．设小时后蓄水池中的水量为吨，则
；
令
＝；则
，即
；
当
，即
时，
，即从供水开始到第6小时时，蓄水池水量最少，只有40吨。
Ⅱ．依题意
，得
；
解得，
，即
，
； 即由
，所以每天约有8小时供水紧张。
22．解：(Ⅰ) 设过焦点F并与轴垂直的弦为直径的圆为圆C/，圆M与曲线C在第一象限的交点为A，圆C/与直线 正方向的交点为B。
∵圆C/截直线的弦长为2
∴
，∴
…………(2分)
由圆锥曲线的第二定义，对于曲线C上的任意点
，有
… (4分) 整理得圆锥曲线C的方程为
…… (6分)
（Ⅱ）当直线
的倾斜角为
时，
，此时双曲线C上无任何两点关于直线对称；
当直线的倾斜角为
时，
，此时双曲线C关于直线
对称，除顶点外，对双曲线上任一点都存在双曲线上另一点关于直线对称，不合要求。……(8分)
当
时，设
，设P
、Q
两点是双曲线C上关于直线的对称点，PQ中点为T
，直线PQ的方程为
，…………(9分)
由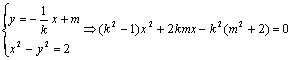
由
由韦达定理及中点坐标公式，求得T点坐标
又T点在直线上，∴ 
，整理得：
…………(12分)
（1）（2）联立得：
。
∴直线的倾斜角的范围是
。…………(14分)