北京师大附中2006年1月高三数学期末模拟试题
一、选择题：
1．（理科做）已知复数
则
为（ ）
（A）
（B）
（C）
（D）
(文科做) 已知
则
的值为 (
)
(A)7
(B)7
（C）
（D）
2．已知函数
在区间[1，2]上的最大值比最小值大2，则
的值为（ ）
（A）2
（B）
（C）
（D）
3．若向量
=
=(1，－1)，则2
的取值范围是( )
(A)
(B)
(C)
(D)[1,3]
4．函数
的反函数是( )
(A)
(B) 
(C) 
(D) 
5．
的展开式中存在常数项,则n的值可以是( )
(A)12 (B)13 (C)11 (D)10
6．已知全集为U, A∩B =B,且
则下列各式中一定错误的是( )
(A) 
CUA =
(B) 
CUA =
(C)
(CUA)
(CUB) = (D)A
CUB
7．棱长为
的正方体,过从每一个顶点引出的三条棱的中点作一个平面切去正方体的一个角,依次切去各角后所剩多面体的表面积为( )
(A) 
(B)
(C) 
(D) 
8．小李进行射击训练,每次射中目标的概率为
,且各次射击相互没有影响,则他射击5次恰好命中3次且恰有2次连续命中的概率为
(A)
(B)
(C)
(D)
二、填空题：
9．不等式
在N中的解集为
,在R中的解集为
.
10．为了由
的图象得到函数
的图象，可以先把所有点的横坐标缩小为原来的
（纵坐标不变），再把所有点向 个单位长度；或者先把所有点向 个单位长度，再把所有点的横坐标缩小为原来的（纵坐标不变）．
11．等比数列
的前项的和为
则常数k的值为 ，此数列的通项公式为
.
12．
为异面直线，P为外一点，下列结论：
①过P必可作平面与均平行；②过P可作唯一直线与均垂直；
③过P必可作直线与均相交；④过P可作平面与均垂直；
⑤过可各作一平面互相平行；⑥过可各作一平面互相垂直.
其中正确结论的编号为 .
13．（理科做）函数
在区间
的最大值为
，最小值为
.
(文科做) 曲线
在点P处的切线和直线
垂直, 则点P的坐标为 ,切线方程为
.
14．一个正三棱柱恰好有一个内切球（即恰好与两底面和三个侧面都相切）和一外接球（即恰好经过三棱柱的6个顶点）；则此内切球、外接球与正三棱柱的体积之比为
：
：
. 。
三．解答题：
15．已知关于
的不等式
的解集为A，且
（1）求实数的取值范围；
（2）求集合A.
16．已知向量=
=
（1）求·及＋;
(2 ) 若
·
＋的最小值为
求
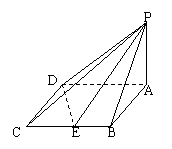
17．如图四棱锥P－ABCD的底面是边长为2的菱形，且∠BAD = 60°，PA⊥平面ABCD，设E为BC的中点，二面角P－DE－A为45°.
(1 ) 求点A到平面PDE的距离;
(2 ) 在PA上确定一点F,使BF∥平面PDE;
(3 ) 求异面直线PC与DE所成的角(用反三角函数表示);
(4 ) 求面PDE与面PAB所成的不大于直二面角的二面角的大小(用反三角函数表示).
 |
18．（（理科做）某同学参加法律知识竞赛，共有4道试题,他答对每道题的概率都是
且回答各题相互独立. 竞赛规定: 参赛者未答题前有底分300分,每答对一题得100分,答错扣100分,一开始即连答错3道题就失去资格自动下场.
(1 ) 求此同学答题数目
的分布列和数学期望;
(2 ) 求此同学最后得分
的分布列和数学期望;
(3 ) 若另有5名同学都与此名同学水平相当,求他们6人中到最后能留在场上的人数
的期望和方差.
(文科做) 在一次招聘面试中,备有10道题,甲能答对其中的6道题,乙能答对其中的8道题,规定每人分别从10道题中随机抽取3道题测试(答完放回),若至少答对2道题者合格.
(1 ) 求甲乙两人至少有一人测试合格的概率;
(2 ) 求甲乙两人中恰有一人测试合格的概率.
19．（理科做）已知函数
（1）求函数
的单调区间；
（2）若
证明：
(文科做)已知
在
时有极大值6，在
时有极小值，求
的值；并求在区间[－3，3]上的最大值和最小值.
20．（13分）如图，把正△ABC分成有限个全等的小正三角形，且在每个小三角形的顶点上都放置一个非零实数，使得任意两个相邻的小三角形组成的菱形的两组相对顶点上实数的乘积相等。设点A为第1行，…，BC为第n行，记点A上的数为
第i行中左起第j个数为
若
（1）求
；
（2）试归纳出
的表达式（用含n，m的式子表示，不必证明）；
（3）记
，证明
北京师大附中2005——2006学年度上学期高三数学
期末模拟试题（06.1）解答
一、
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 | C | D | A | B | C | D | B | C |
二、9．{0，1，2，3，4}，
.
10. 
, 
.
11. － 2 , 
.
12. ②⑤⑥.
13. (理)
, 0 . (文)(1,－2),
.
14. 
, 
.
三、15．（1）
，当
时，有
即
，即的取值范围是
（2）
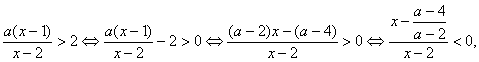
由（1）知
，又由
知：
当
时，
则集合
；
当
时，原不等式的解集A为空集；
当
时，
，则集合
16．（1）a·b = 
a＋b
。
（2）
当
时，
时）；
当
时，
时）；
当
时，
时）。
17．（1）DE为正△BCD的中线，DE⊥BC，∴DE⊥AD，又PA⊥平面ABCD，DE⊥PD，∠PDA = 45°，作AH⊥PD于H，则DE⊥AH，∴AH⊥平面PDE，PA = AD = 2，
AH =
，即点A到平面PDE的距离为。
（2）F为PA的中点，可证BF∥EH，∴BF∥平面PDE。
（3）延长AD到G，使DG = EC，连CG、PG，可证CG∥DE，△PCG中，CG =
PC =
PG =
PC与DE所成角为
（4）设
连PM，作HO⊥PM于O，连AO，可证∠AOH为所求二面角的平面角，AO =
18．（理）（1）
|
| 3 | 4 |
| P |
|
|
（2）
分布列为
|
| 0 | 100 | 300 | 500 | 700 |
| P |
|
|
|
|
|
（3）～ B（6，
，
（文）设A表示事件“甲合格”，B表示事件“乙合格”，
（1） 所求概率为P（A+B）= 
（2） 所求概率为
19．（理）（1）
时，
单调递增；
时，
单调递减。
（2）
即
；
令
则
当
时，
当时，
即
综上知，当
时，
（文）（1）
由条件知
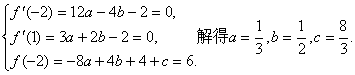
（2）
| x | －3 | (－3,－2) | －2 | (－2,1) | 1 | (1,+ | 3 |
|
| ＋ | 0 | － | 0 | ＋ | ||
|
| 4 | ↗ | 6 | ↘ |
| ↗ | 10 |
由上表知，在区间[－3，3]上，当时，
时，
20．（1）
，
（2）
是公比为的等比数列，
是公比为的等比数列，
（3）由（2）知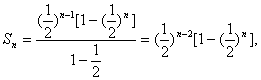
又
