北京市八中2005—2006学年度上学期高三调研模拟试卷
数学(文科)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至2页,第Ⅱ卷3至6页,卷面共150分,考试时间120分钟.
第Ⅰ卷(选择题,共50分)
注意事项:
1.答第Ⅰ卷前,考生务必将自己的准考证号、试场号用钢笔或圆珠笔填写在答题卷上. 2.每小题选出答案后,用钢笔或圆珠笔填写在答题卷上.
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合![]() ,那么
,那么![]()
A.![]() B.
B. ![]() C.
C.![]() D.
D.![]()
2.已知等差数列![]() 中,
中,![]() 的值是
的值是
A.15 B.30 C.31 D.64
3.设![]() ,则
,则
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.如果![]() 是等比数列,则
是等比数列,则
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5.函数![]() ,在
,在![]() 上最小值为
上最小值为
A.0 B.-2
C.-1 D.![]()
6.![]() 反函数是
反函数是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
7.下列函数既是奇函数,又在区间![]() 上单调递减的是
上单调递减的是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
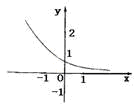 8.函数
8.函数![]() 的图象如图,其中a、b为常数,则下列结论正确的是
的图象如图,其中a、b为常数,则下列结论正确的是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
9.下列判断错误的是
A.命题“若q则p”为真命题,则![]() 为
为![]() 成立的必要条件
成立的必要条件
B.“![]() ”是“
”是“![]() ”的充要条件
”的充要条件
C.命题“若![]() ,
,![]() 方程
方程![]() 的根,则
的根,则![]() 或
或![]() ”的否命题为“若
”的否命题为“若![]() ,
,![]() 不是方程
不是方程![]() 的根,则
的根,则![]() 且
且![]() ”
”
D.命题“![]() 且
且![]() ”为真命题
”为真命题
10.设函数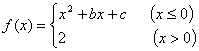 ,若
,若![]() ,
,![]() ,则关于
,则关于![]() 的方程
的方程![]() 的解的个数为
的解的个数为
A.1 B.2 C.3 D.4
天星 教育网
第Ⅱ卷(非选择题 共100分)
注意事项:
1.第Ⅱ卷共6页,用钢笔或圆珠笔直接答在答题卷中.
2.答卷前将密封线内的项目填写清楚.
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在答卷中的横线上.
11.曲线![]() 在点
在点![]() 处的切线方程是___________.
处的切线方程是___________.
12.设![]() ,则
,则![]() .
.
13.若数列![]() 满足
满足![]() ,且
,且![]() ,则
,则![]() .
.
14.设![]() 是定义在
是定义在![]() 上的奇函数,且
上的奇函数,且![]() 的图象关于直线
的图象关于直线![]() 对称,则
对称,则![]() _______________.
_______________.
三、解答题:本大题共6小题,84分.解答应写出文字说明,证明过程或演算步骤.
15.(本小题满分14分)
已知![]() 和
和![]() ,试问
,试问![]() 是
是![]() 的什么条件?
的什么条件?
16.(本小题满分14分)
设![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的值.
的值.
17.(本小题满分14分)
已知![]() 是等差数列,
是等差数列,![]() 是等比数列,且
是等比数列,且![]()
![]() ,
,![]() ,又
,又![]()
![]() .
.
(1)求数列![]() 的通项公式和数列
的通项公式和数列![]() 的通项公式;
的通项公式;
(2)设![]() ,其中
,其中![]() ,求
,求![]() 的值.
的值.
18.(本小题满分14分)
已知数列![]() 的前
的前![]() 项和为
项和为![]() .
.
(1)试写出![]() 中
中![]() 与
与![]() 的关系式,并求数列
的关系式,并求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,如果对一切正整数
,如果对一切正整数![]() 都有
都有![]() ,求
,求![]() 的最小值.
的最小值.
19.(本小题满分14分)
某工厂生产某种零件,每个零件的成本为![]() 元,出厂单价为
元,出厂单价为![]() 元.该厂为鼓励销售商订购,决定当一次订购量超过
元.该厂为鼓励销售商订购,决定当一次订购量超过![]() 个时,每多订购
个时,每多订购![]() 个,订购的全部零件的出厂单价就降价
个,订购的全部零件的出厂单价就降价![]() 元,但实际出厂单价不能低于
元,但实际出厂单价不能低于![]() 元.
元.
(1)当一次订购量为多少时,零件的实际出厂单价恰降为![]() 元?
元?
(2)设一次订购量为![]() 个,销售的利润为
个,销售的利润为![]() 元,写出函数
元,写出函数![]() 的表达式。(工厂售 出一个零件的利润=实际出厂单价-成本)
的表达式。(工厂售 出一个零件的利润=实际出厂单价-成本)
20.(本小题满分14分)
已知![]() 是函数
是函数![]() 的一个极值点,其中
的一个极值点,其中![]() ,
,
(1)求![]() 与
与![]() 的关系式;
的关系式;
(2)求![]() 的单调区间;
的单调区间;
(3)若![]() ,求证:函数
,求证:函数![]() 的图象与
的图象与![]() 轴只有一个交点.
轴只有一个交点.
参考答案及评分标准
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | D | A | A | D | A | B | D | D | B | C |
11. ![]() . 12. 1 13. 12
14.0
. 12. 1 13. 12
14.0
15. 由命题![]() 得:
得:![]() 或
或![]() ;天星 教育网
;天星 教育网
由命题![]() 得:
得:![]() 或
或![]()
则![]() 为:
为:![]() ;
;![]() 为:
为:![]()
可知:![]() 反之则不成立。
反之则不成立。
所以![]() 是
是![]() 的充分不必要条件。
的充分不必要条件。
16.由题意知:![]()
(1) 当![]() 时,
时,![]() ,
,
(i)![]() ,即方程
,即方程![]() 无实数根
无实数根
![]() 得
得![]()
(ii)![]() ,即方程
,即方程![]() 有唯一的根
有唯一的根![]()
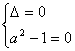 得
得![]()
(iii)![]() 即方程
即方程![]() 有唯一的根
有唯一的根![]()
![]() 得
得![]()
(ⅳ)![]() 即方程
即方程![]() 有两个实数根
有两个实数根![]()
![]() 得
得![]()
综上所述,![]() 的取值范围为
的取值范围为![]() 或
或![]()
(2)当![]() 时,即
时,即![]()
则![]() ,即方程
,即方程![]() 有两个实数根
有两个实数根![]()
![]() 得
得![]()
17.(1)由题意已知![]() 是等差数列,
是等差数列,![]() 是等比数列,且
是等比数列,且![]()
![]() ,
, ![]() ,所以
,所以![]() ,则等比数列的通项公式为
,则等比数列的通项公式为![]()
又![]()
![]() .解得
.解得![]() ,所以等差数列的通项公式为
,所以等差数列的通项公式为![]()
(2)![]()
18.(1)![]() ,
,
![]() ,
,![]()
![]() 又当
又当![]() 时,
时,![]() ,即
,即![]() ,
,
对于正整数![]() 都有
都有![]() ,
,![]() 是等差数列
是等差数列![]() .
.
(2)![]() ,
,
![]()
![]()
![]() ,
,![]()
![]() 数列
数列![]() 中最大值是
中最大值是![]()
![]()
![]() 的最小值为
的最小值为![]() .
.
19.(1)设每个零件的实际出厂价恰好降为51元时,一次订购量为![]() 个,则
个,则 ![]() ,
, ![]() 则
则![]()
所以,当一次定购量为550个时,每个零件的实际出厂价格恰好降为51元.
(2)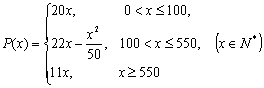
20.(1)![]() 因为
因为![]() 是函数
是函数![]() 的一个极值点,所以
的一个极值点,所以![]() , 即
, 即![]() ,所以
,所以![]()
(2)由(I)知,![]() =
=![]()
当![]() 时,有
时,有![]() ,当
,当![]() 变化时,
变化时,![]() 与
与![]() 的变化如下表:
的变化如下表:
|
|
|
|
| 1 |
|
|
|
| 0 |
| 0 |
|
|
| 单调递减 | 极小值 | 单调递增 | 极大值 | 单调递减 |
故有上表知,当![]() 时,
时,![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,在
单调递增,在![]() 上单调递减.
上单调递减.
(3)证明:![]() ,当
,当![]() 时,
时,![]() ,则函数
,则函数![]() 的图像在
的图像在![]() 上和x轴没有交点,在
上和x轴没有交点,在![]() 上单调递减,与x轴有一个交点,综上所述,若
上单调递减,与x轴有一个交点,综上所述,若![]() ,函数
,函数![]() 的图象与
的图象与![]() 轴只有一个交点.
轴只有一个交点.