北京市第二中学2005—2006学年度第一学期高三年级统一调研模拟
数学试卷
一、选择题:(每题5分,共60分)
1.设函数![]() 满足
满足![]() 且当
且当![]() 时,
时,![]() 是增函数,则
是增函数,则![]()
![]() 的大小关系是 ( )
的大小关系是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.设偶函数![]() 上递增函数,则
上递增函数,则![]() 的大小关系
的大小关系
是 ( )
A.![]() B.
B.![]()
C.![]() D.不确定
D.不确定
3.函数![]() 在[0,1]上是减函数,则a的取值范围 ( )
在[0,1]上是减函数,则a的取值范围 ( )
A.(0,1) B.(1,2) C.(0,2) D.![]()
4.已知![]() ,设p:函数
,设p:函数![]() 在R上单调递减。
在R上单调递减。![]() 不等式的解集为R。
不等式的解集为R。
如果p和Q有且仅有一个正确,求c的取值范围 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.已知:![]() 则有 ( )
则有 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6.设函数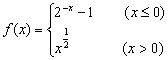 若
若![]() 的取值范围是 ( )
的取值范围是 ( )
A.(-1,1) B.(-1,+∞)
C.![]() D.
D.![]()
7.定义在R上的函数![]() 满足
满足![]() ,则当
,则当
![]() 的最小值是 ( )
的最小值是 ( )
A.-1 B.![]() C.
C.![]() D.
D.![]()
8.已知方程![]() 的四个根组成一个首相为
的四个根组成一个首相为![]() 的等差数列,则
的等差数列,则
m-n= ( )
A.1 B.![]() C.
C.![]() D.
D.![]()
9.在不等边△ABC中,a为最大边,且![]() 则
则![]() 的范围是 ( )
的范围是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.若![]() 的值等于 ( )
的值等于 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.已知:![]() ,则实数a的取值范围
,则实数a的取值范围
是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
12.设集合![]() 则实数a的取值范围是( )
则实数a的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空:(每空4分,共16分)
13.方程![]() 对所有
对所有![]() 有解,则a的范围是
.
有解,则a的范围是
.
14.已知:![]() 的大小关系是
.
的大小关系是
.
15.计算![]() .
.
16.若函数![]() 的定义域为[0,1],则
的定义域为[0,1],则![]() 的定义域为
.
的定义域为
.
三、解答题:(共74分)
17.(12分)某公司规定:一个车间,班组在一个季度里,如果1个月安全生产无事故且完
成任务,则可得奖金900元;如果有2个月安全生产无事故且完成任务则可得奖金2100
元;如果有3个月安全生产无事故且完成任务,则可得奖金3300元;如果3个月都出
现安全事故且未完成任务,则不得奖金。假如某车间每月能否完全生产无事故且完成任
务是等可能的。试分析该公司的这项规定是否有利于调动广大职工的积极性,并说明理
由.
18.(12分)已知函数![]() 在R上为减函数,求a的取值范围.
在R上为减函数,求a的取值范围.
![]() 19.(12分)已知集合
19.(12分)已知集合![]() B求实
B求实
数k的取值范围.
20.(12分)设![]() 是定义在
是定义在![]() 上的减函数,已知
上的减函数,已知![]()
对于![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
21.(12分)已知函数![]()
(1)求![]() 的最小正周期;
的最小正周期;
(2)若![]() ,试求
,试求![]() 的最大值,最小值;
的最大值,最小值;
(3)若![]() ,试求满足不等式
,试求满足不等式![]() 的自变量
的自变量![]() 的集合.
的集合.
22.(14分)已知函数![]()
(1)求![]() 的解析式;
的解析式;
(2)设数列![]() 的通项公式为
的通项公式为![]() 其前n项的和为Sn,试求
其前n项的和为Sn,试求![]() ;
;
(3)设![]() 问:是否存在实数
问:是否存在实数![]() ,使
,使![]()
上为减函数且(-1,0)上是增函数?若存在求出实数![]() 的值和
的值和![]() 的单调区间,
的单调区间,
以及![]() 的极值;若不存在,请说明理由.
的极值;若不存在,请说明理由.
数学参考答案
一、选择题(每题5分,共60分)
1.D 2.B 3.B 4.D 5.D 6.D 7.D 8.B 9.C 10.C 11.C 12.B
二、填空:(每空4分,共16分)
13.![]() 14.
14.![]() 15.
15.![]() 16.
16.![]()
三、解答题:
17.![]()
![]() =1537.5(元) 有利于调动职工的积极性
=1537.5(元) 有利于调动职工的积极性
18.![]()
由![]()
当![]() 时合题意
时合题意 ![]()
![]() 19.
19.![]() B
B ![]()
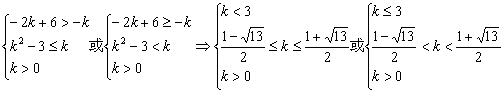
![]()
|
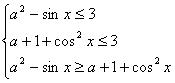
由①得:![]() 由②得
由②得![]()
由③得:![]()
![]()
![]()
①②③取交集得:![]()
21.(1)![]() (2)最大值
(2)最大值![]() ,最小值
,最小值![]() (3)
(3)![]()
![]()
22.①![]()
②![]()
③![]() ,列表分析知,存在实数
,列表分析知,存在实数![]() ,
,
使![]() 递增 在
递增 在![]() 递减
递减
当![]() 极小值-3
极小值-3
当![]() 极大值-2.
极大值-2.