北京市东城区高三年级综合练习(一)
数 学 试 卷
(文史类)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分.考试时间120分钟.
第Ⅰ卷(选择题 共40分)
参考公式:
三角函数的和差化积公式 正棱台、圆台的侧面积公式
![]()
![]()
![]() 其中c′、c分别表示上、下底面周长,l表示
其中c′、c分别表示上、下底面周长,l表示
![]() 斜高或母线长、台体的体积公式:
斜高或母线长、台体的体积公式:
![]()
![]()
其中S′、S分别表示上、下底面积,h表示高.
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.“![]() ”是“
”是“![]() ”的 ( )
”的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
2.若![]() 则
则![]() 的值是 ( )
的值是 ( )
A.-a B.a C.![]() D.-
D.-![]()
3.已知复数![]() 的最大值是 ( )
的最大值是 ( )
A.3-![]() B.3 C.3+
B.3 C.3+![]() D.2+
D.2+![]()
4.已知直线l⊥平面α,直线m![]() 平面β,有下面四个命题:
平面β,有下面四个命题:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中正确的两个命题的序号是 ( )
,其中正确的两个命题的序号是 ( )
A.①与② B.③与④ C.②与④ D.①与③
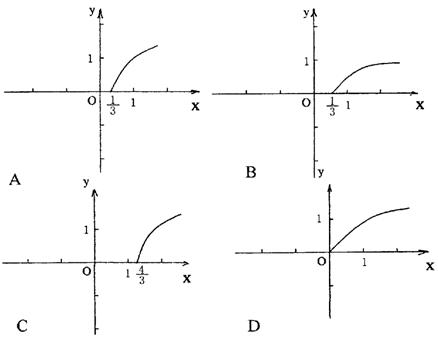
|
( )
6.已知![]() 是等差数列,a1=-9,S3=S7,那么使其前n项和Sn最小的n是 ( )
是等差数列,a1=-9,S3=S7,那么使其前n项和Sn最小的n是 ( )
A.4 B.5 C.6 D.7
7.直线l与直线y=1,x-y-7=0分别交于P,Q两点,线段PQ的中点为(1,-1),则直线l的斜率为 ( )
A.![]() B.
B.![]() C.-
C.-![]() D.-
D.-![]()
|
要使此饭店每天收入最高,则每间房价应定为 ( )
A.90元 B.80元 C.70元 D.60元
第Ⅱ卷(非选择题 共110分)
二、填空题:本大题共6小题,每小题5分,共30分.把答案填在题中横线上.
9.已知集合M=![]() ,那么M∩N等于
.
,那么M∩N等于
.
10.一张厚度为0.1mm的矩形纸,每次将此纸沿对边中点连线对折,一共折叠20次(假定这样的折叠是可以完成的),这时折叠后纸的总厚度h1与一座塔的高度h2=100m的大小关系为h1 h2.
11.有5部各不相同的电话参加展览,排成一行,其中有2部不同的电话来自同一个厂家,则此2部电话恰好相邻的排法总数是 (用数字作答).
12.双曲线![]() 的焦点坐标是
和 .
的焦点坐标是
和 .
13.空间四边形ABCD中,AB=CD,且AB与CD成60°角,E、F分别为AC,BD的中点,则EF与AB所成角的度数为 .
14.某纺织厂的一个车间有n(n>7,n∈N)台织布机,编号分别为1,2,3,……,n,该车间有技术工人n名,编号分别为1,2,3,……,n.定义记号![]() ,如果第i名工人操作了第j号织布机,此时规定
,如果第i名工人操作了第j号织布机,此时规定![]() =1,否则
=1,否则![]() =0.若第7号织布机有且仅有一人操作,则
=0.若第7号织布机有且仅有一人操作,则
![]() ;若
;若![]() 说明:
.
说明:
.
三、解答题:本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤.
15.(本小题满分12分)
解关于x的不等式![]()
16.(本小题满分12分)
△ABC的内角A、B、C满足![]() ,试判断△ABC的形状,并加以证明.
,试判断△ABC的形状,并加以证明.
17.(本小题满分14分)
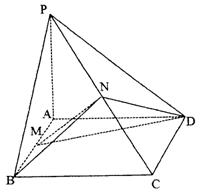
已知:ABCD是矩形,设PA=a,PA⊥平面ABCD.M、N分别是AB、PC的中点.
(Ⅰ)求证:MN⊥AB;
(Ⅱ)若平面PCD与平面ABCD所成的二面角为45°,且PD=AB,求证:平面MND⊥平面PCD;
(Ⅲ)在(Ⅱ)的条件下,求三棱锥N—AMD的体积.
|
18.(本小题满分14分)
为合理用电缓解电力紧张,某市将试行“峰谷电价”计费方法,在高峰用电时段,即居民户每日8时至22时,电价每千瓦时为0.56元,其余时段电价每千瓦时为0.28元.而目前没有实行“峰谷电价”的居民户电价为每千瓦时0.53元.若总用电量为S千瓦时,设高峰时段用电量为x千瓦时.
(Ⅰ)写出实行峰谷电价的电费![]() 及现行电价的电费
及现行电价的电费![]() 的函数解析式及电费总差额
的函数解析式及电费总差额![]() 的解析式;
的解析式;
(Ⅱ)对于用电量按时均等的电器(在任何相同的时间内,用电量相同),采用峰谷电价的计费方法后是否能省钱?
(Ⅲ)你认为每家每户是否都适合“峰谷电价”的计费方法?(只回答是或不是)
19.(本小题满分14分)
已知椭圆C的中心在原点,左焦点为F1,其右焦点F2和右准线分别是抛物线![]() 的顶点和准线.
的顶点和准线.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若点P为椭圆C上的一个动点,当∠F1PF2为钝角时,求点P横坐标的取值范围.
20.(本小题满分14分)
设数列![]() 是以a为首项,q为公比的等比数列,令
是以a为首项,q为公比的等比数列,令![]()
![]()
(Ⅰ)试用a,q表示bn和cn;
(Ⅱ)若![]() 试比较
试比较![]() 的大小;
的大小;
(Ⅲ)是否存在实数对(a,q),其中![]() ,使
,使![]() 成等比数列,若存在,求出实数对(a,q)和
成等比数列,若存在,求出实数对(a,q)和![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
北京市东城区2004年高三年级综合练习(一)
数学参考答案(文史类)
一、选择题
1.A 2.A 3.C 4.D 5.A 6.B 7.C 8.B
二、填空题
9.{1,2} 10.> 11.48
12.![]() (答对一个3分,答对两个5分)
(答对一个3分,答对两个5分)
13.60°或30° 14.1,(2分) 第三名工人操作了2台织布机(3分)
三、解答题
15.(1)原不等式等价于![]() 由于
由于![]() 恒成立,
恒成立,
∴![]() …………6分
…………6分
当a>0时,![]() ;当a=0时,
;当a=0时,![]() ;
;
当a<0时,![]() ;…………12分
;…………12分
16.解:△ABC是等腰三角形.在△ABC中,A+B+C=π,由题设![]()
∴![]()
∴sinBsinC+cosBcosC=1. 即cos(B-C)=1…………7分
∵![]() 从而B-C=0,即B=C.
从而B-C=0,即B=C.
∴△ABC是等腰三角形.………………12分
17.(Ⅰ)连结AC,AN. 由BC⊥AB,AB是PB在底面ABCD上的射影. 则有BC⊥PB.
|
即![]() .…………2分
.…………2分
由PA⊥底面ABCD,有PA⊥AC,
则AN是Rt△PAC斜边PC的中线,
即![]() ………………2分
………………2分
![]() ………………4分
………………4分
又∵M是AB的中点,
![]() …………5分
…………5分
(Ⅱ)由PA⊥平面ABCD,AD⊥DC,根据三垂线定理,有PD⊥DC.
则∠PDA为平面PCD与平面ABCD所成二面角的平面角.…………7分
∴∠PDA=45°由PA=AD=BC,不难算出PM=MC,则有MN⊥PC.
又由AB=PD=DC,则有DN⊥PC. ∴PC⊥平面MND. 又PC![]() 平面PCD,
平面PCD,
∴平面MND⊥平面PCD.…………10分
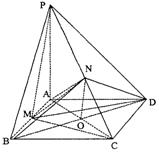
![]() (Ⅲ)连结BD交AC于O,连结ON,则NO
(Ⅲ)连结BD交AC于O,连结ON,则NO ![]() PA.
PA.
且NO⊥平面AMD,由PA=AD=a,![]()
![]() .……………………………14分
.……………………………14分
18.(Ⅰ)若总用电量为S千瓦时,设高锋时段用电量为x千瓦时,则低谷时段用电量为
(S-x)千瓦时.
![]() ………………3分
………………3分
![]() ………………4分
………………4分
电费总差额![]() …………6分
…………6分
(Ⅱ)可以省钱.
令![]() 即
即![]() …………9分
…………9分
对于用电量按时均等的电器而言,高峰用电时段的时间与总时间的比为
![]() .
.
所以用电量按时均等的电器采用峰谷电价的计费方法后能省钱.…………12分
(Ⅲ)不是.………………14分
19.(Ⅰ)抛物线![]() 的顶点为(4,0).
的顶点为(4,0).
准线方程为![]() .………………3分
.………………3分
设椭圆方程为![]() .
.
则有![]() ,可得
,可得![]() .
.
∴椭圆方程为![]() ………………7分
………………7分
(Ⅱ)设P点坐标为![]() 由椭圆的第二定义,有
由椭圆的第二定义,有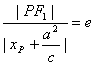 ,
,
![]() 同理
同理![]()
![]() 在△PF1F2中,
在△PF1F2中,
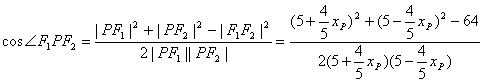
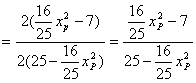 .……………………11分
.……………………11分
![]() 是钝角
是钝角 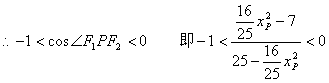 .
.
解得![]() .……………………14分
.……………………14分
20.(1)当q=1时,![]() ………………2分
………………2分
当![]() ,
,
![]() ……5分
……5分
(2)![]()
因为![]() ,
,
由已知![]() ,
,
则![]() .
.
又![]() .
.
所以![]() . 即
. 即![]() ……………………9分
……………………9分
(3)![]() 成等比数列,则令
成等比数列,则令
|
|
 …………………………11分
…………………………11分
由②得![]() ,代入①得
,代入①得![]() .
.
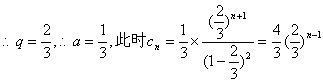 .
.
所以存在实数对![]() ,使
,使![]() 成为以
成为以![]() 为首项,
为首项,![]() 为公比的等比数列.
为公比的等比数列.
………………………………14分