北京市丰台区2006年高三数学（文科）统一练习二 （2006．5）
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，第Ⅰ卷1至2页，第Ⅱ卷3至9页，共150分。考试时间120分钟。
第Ⅰ卷（选择题 共40分）
注意事项：
1．答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上。
2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其他答案标号。不能答在试卷上。
一、选择题 ：本大题共8个小题，每小题5分，共40分。在每个小题列出的四个选项中，选出符合题目要求的一项。
(1) 设
是集合A到集合B的映射，若A＝｛－2，0，2｝，则
可能是
(A) ｛0｝ (B) ｛2｝ (C) ｛0，2｝ (D) ｛－2，0｝
(2) 设
(A)
(B) －
(C) 
(D)
－
(3) 连结椭圆
短轴的一个顶点与两个焦点组成正三角形,则椭圆的准线方程为
(A) 
(B) 
(C) 
(D) 
(4) 函数
(A)
0
(B)1
(C) 
(D) 
(5) 在等差数列
中，若
的值为
(A)17 (B)16 (C)15 (D)14
(6) 某校学生会由高一4名学生、高二5名学生、高三4名学生组成，现从中选出2名学生，参加一次活动，则此2名学生不属于同一个年级的选出方法有
(A)640种 (B)56种 (C)40种 (D)36种
(7) 当
，则a的取值范围是
(A)（1，
）
(B)（
，1）
(C) （，1）
（1，） (D) （0，1）（1，）
(8) 
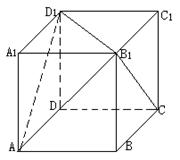如图，设正方体ABCD－A1B1C1D1的棱长为1，则直线B1C与平面AB1D1所成的角是
(A)
(B)
(C)
(D)
第Ⅱ卷（ 共110分）
注意事项：1．用钢笔或圆珠笔将答案直接写在试卷上。
2．答卷前将密封线内的项目填写清楚。
| 题 号 | 一 | 二 | 三 | 总分 | |||||
| 15 | 16 | 17 | 18 | 19 | 20 | ||||
| 分 数 | |||||||||
| 得分 | 评卷人 |
|
|
二、填空题 ：本大题共6小题，每小题5分，共30分。把答案填在题中横线上
(9)直线x+y=0与直线3x+3y－5=0的位置关系是 ，原点到直线3x+3y－5=0的距离等于 。
(10)
的展开式中的常数项是
。
(11) 要从1000个（其中白球有50个）球中抽取100个进行抽样分析，如果用分层抽样的方法对球进行抽样，则应抽取白球的个数是 。
(12) 已知O是坐标原点，A(1, 2),B(5 , 1),C(x, 4),设AC的中点为D，若∥，则x＝ 。
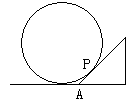(13) 如图，水平地面上有一个大球，现有如下方法测量球
的大小：用一个锐角为45°的三角板，斜边紧靠球面，一
条直角边紧靠地面，并使三角板与地面垂直，P为三角板与
球的切点，如果测得PA＝2，则球的表面积为
。
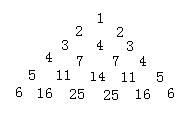
(14) 如图，它满足：
（1）第n行首尾两数均为n；
（2）表示它的递推关系类似杨辉三角，
则第n行（
2）的第二个数是
。
三、解答题 ：本大题共6小题，共80分。解答应写出文字说明，证明过程或演算步骤。
| 得分 | 评卷人 |
|
| 1 |
(15) （本小题共13分）
已知函数
，它反函数的图像过点（－1，2）。
（Ⅰ）求函数f(x)的表达式；
（Ⅱ）设k>1,解关于x的不等式：
。
| 得分 | 评卷人 |
|
|
(16)（本小题共14分）
已知函数
，且f(x)在
处有极大值为2。
（Ⅰ）求函数f(x)的单调区间；
（Ⅱ）设
，试比较a，b的大小。
| 得分 | 评卷人 |
|
|
(17) （本小题共13分）
有一批产品出厂前要进行4项指标抽检，如果有2项指标不合格，那么这批产品就不能出厂，已知每项指标抽检是互相独立的，且每项指标出现不合格的概率是
。
(Ⅰ)求这批产品不能出厂的概率；
(Ⅱ)求直至4项指标全部检验完毕，才能确定该产品能否出厂的概率。
| 得分 | 评卷人 |
|
|
(18) （本小题共14分）
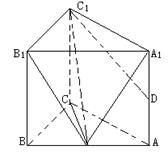如图，直三棱柱ABC－A1B1C1的侧棱长6，底面△ABC是等腰直角三角形，∠ACB＝90°，AC＝2，D，E分别为AA1，AB的中点。
(Ⅰ) 求异面直线A1B1和C1D所成的角；
(Ⅱ) 求证A1E⊥C1D ;
(Ⅲ) 求点D到平面B1C1E的距离。
| 得分 | 评卷人 |
|
| 1 |
(19) （本小题共14分）
已知数列满足：
，且
，
。
(Ⅰ)求证数列
是等差数列，并求数列，
的通项公式；
(Ⅱ)设
,求数列
的前年项和
.
| 得分 | 评卷人 |
|
|
(20) （本小题共12分）
已知焦点在x轴上的双曲线C的两条渐近线过原点，且两条渐近线与以点A（0，）为圆心，1为半径的圆相切，双曲线C的一个焦点与点A关于直线y=x对称。
(Ⅰ)求双曲线C的方程；
(Ⅱ)设直线
与双曲线C的左支交于A，B两点，另一直线
经过M（－2，0）和AB的中点，求直线在y轴上截距b的取值范围。
丰台区2006年高三统一练习二参考答案
数 学 （文科）
一、选择题 ：本大题共8个小题，每小题5分，共40分。
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 | C | A | A | D | B | B | C | B |
二、填空题 ：本大题共6小题，每小题5分，共30分。
(9) 平行 
(10)
672 (11) 5 (12) 11 (13) 
(14)
三、解答题 ：本大题共6小题，共80分。解答应写出文字说明，证明过程或演算步骤。
(15) （本小题共13分）
解：(Ⅰ)依题意函数f(x)过点（2，－1），有
………4分
(Ⅱ) 解
………………6分
当k>3时， 
…………………8分
当1<k<3时，
…………………10分
当k＝3时 ，
…………………12分
所以，当k>3时，不等式的解集为
；当1<k<3时，不等式的解集为
；
当k＝3时，不等式的解集为空集。 …………………13分
(16)（本小题共14分）
解：(Ⅰ)
……………2分
依题意 
…………………4分
当
所以函数f(x)的单调增区间为（－1，1）；
函数f(x)的单调减区间为(1，2
,
…………………10分
因为 
函数f(x)在区间（－1，1）为增函数
所以 
即
…………………14分
(17) （本小题共13分）
解：(Ⅰ)4项抽检中没有出现不合格的概率为
…………………3分
4项抽检中恰有1项不合格的概率为
…………………6分
则这批产品不能出厂的概率为1－－＝0.0523………9分
(Ⅱ)由题意可知， 前3项抽检中恰有1项不合格的
概率为
……………13分
(18) （本小题共14分）
解：(Ⅰ)取CC1的中点F，连结AF，
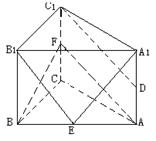则AF∥C1D，，
……………2分
所以 ∠BAF为异面直线A1B1和C1D所成的角 ………3分
又 AC=2，AA1＝2， AB＝2，
在 Rt△AEF中，
所以
即异面直线A1B1和C1D所成的角为
………………5分
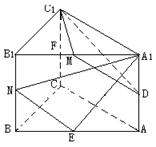(Ⅱ) 取A1B1,BB1的中点M，N，连结C1M，DM，EN，A1N，
又直三棱柱ABC－A1B1C1且底面△ABC是等腰直角三角形
所以 C1M⊥A1B1 ，则有C1M⊥平面A1B1BA，………7分
所以 DM即为C1D在平面A1B1BA上的射影
又在△NEA1中，NE＝
，EA1＝
，NA1＝3
可知 △NEA1为直角三角形，且∠A1EN＝90°，即A1E⊥NE …………8分
又NE∥DM， 所以 A1E⊥DM，由三垂线定理知 A1E⊥C1D …………10分
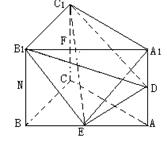(Ⅲ)连结DB1，DE，在四棱锥D－B1C1E中，
设点D到平面B1C1E的距离为h，
而点C1到平面B1DE的距离为
又
解得 
点D到平面B1C1E的距离为
…………………14分
(19) （本小题共14分）
解：(Ⅰ)由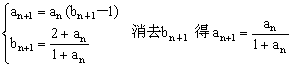
…………………2分
变形为 
…………4分
……………8分
(Ⅱ)
，利用错位相减法可求得
……………14分
（20）（本小题共12分）
解：(Ⅰ)设双曲线C的渐近线方程为y=kx ,又该直线与圆
相切
所以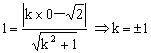 
…………2分
可设双曲线C的方程为
又双曲线C的一个焦点为（，0），
…………4分
所求双曲线C的方程为 
(Ⅱ)由 
…………6分
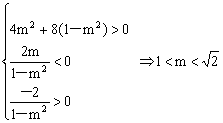………… 9分
线段AB的中点为
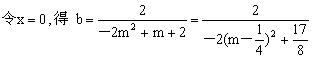…………11分
所以 直线在y轴上截距b
…………12分