北京市海淀区2006年高三数学二模试题（理科）
一．选择题：
1．设全集U=R，集合M={x x>0}，N={x x2≥x}，则下列关系中正确的是（ ）
（A）
（B）
（C）
（D）
2．等比数列前3项依次为：1，a，
，则实数a的值是（ ）
（A）
（B）
（C）－
（D）或－
3．为了得到函数
的图象，可以将函数
的图象（ ）
（A）向右平移
个长度单位 （B）向左平移个长度单位
（C）向右平移
个长度单位 （D）向左平移个长度单位
4．若直线l：ax+by=1与圆C：x2+y2=1有两个不同的交点，则点P(a，b)与圆C的位置关系是（ ）
（A）点在圆上 （B）点在圆内 （C）点在圆外 （D）不能确定
5．若α、β是两个不同的平面，m、n是两条不同的直线，则下列命题不正确的是（ ）
（A）α//β，m⊥α，则m⊥β （B）m//n，m⊥α，则n⊥α
（C）n//α，n⊥β，则α⊥β （D）α 
β=m，n与α、β所成的角相等，则m⊥n
 |
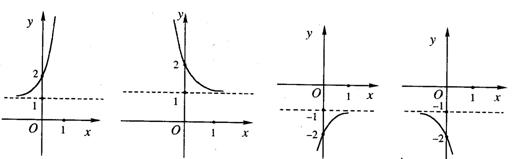6．函数g(x)图象与函数f(x)=
的反函数的图象关于原点对称，则函数g(x) 图象大致为（ ）
（A） （B） （C） （D）
7．若f(x)=ax2+bx+c (a>0，x∈R)，f(－1)=0，则“b<－2a”是“f(2)<0”的（ ）
（A）充要条件 （B）充分不必要条件 （C）必要不充分条件 （D）既不充分也不必要条件
8．为迎接2008年北京奥运会，某校举行奥运知识竞赛，有6支代表队参赛，每队2名同学，若12名参赛同学中有4人获奖，且这4人来自3个不同的代表队，则不同获奖情况种数共有（ ）
（A）
（B）
（C）
（D）
二．填空题：
9．
=
。
10．在同一时间内，对同一地域，市、县两个气象台预报天气准确的概率分别为
、
，两个气象台预报天气准确的概率互不影响，则在同一时间内，至少有一个气象台预报准确的概率是
。
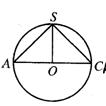
11．正四棱锥S－ABCD内接于球O，过球心O的一个截面如图，棱锥的底面边长为a，则SC与底面ABCD所成角的大小为 ；球O的表面积为 。
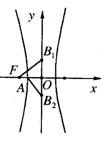12．如图双曲线C的中心在原点，虚轴两端点分别为B1、B2，左顶点和左焦点分别为A、F，若
，则双曲线C的离心率为
。
13．若函数
(a，b∈R)的定义域为R，则3a+b的取值范围是
。
 |
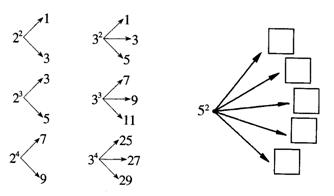14．对大于或等于2的自然数m的n次幂进行如下方式的“分裂”，
仿此，52“分裂”中最大的数是 ，若m3的“分裂”中最小的数是211，则m的值为 。
三．解答题：
15．在△ABC中A、B、C所对的边的长分别为a、b、c，已知向量
，
，满足
，b+c=
a.
（I）求A的大小；
（II）求
的值。
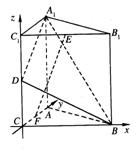
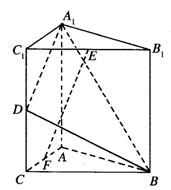16．如图，直三棱柱A1B1C1－ABC中，C1C=CB=CA=2，AC⊥CB，D、E分别是棱C1C、B1C1的中点，
（I）求点B到平面A1C1CA的距离；
（II）求二面角B－A1D－A的大小；
（III）在线段AC上是否存在一点F，使得EF⊥平面A1BD？若存在，确定其位置并证明结论；若不存在，说明理由。
17．已知函数f(x)=mx3+nx2 (m、n∈R，m≠0)，函数y=f(x)的图象在点(2，f(2))处的切线与x轴平行，
（I）用关于m的代数式表示n；
（II）求函数f(x)的单调递增区间；
（III）若x1>2，记函数y=f(x)的图象在点M(x1，f(x1))处的切线为l，设l与x轴的交点为(x2，0)，证明：x2≥3.
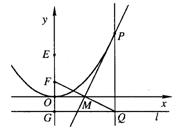
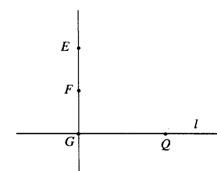
18．如图，平面内的定点F到定直线l的距离为2，定点E满足：
=2，且EF⊥l于G，点Q是直线l上一动点，点M满足：
，点P满足：
，
，
（I）建立适当的直角坐标系，求动点P的轨迹方程；
（II）若经过点E的直线l1与点P的轨迹交于相异两点A、B，令∠AFB=θ，当
时，求直线l1的斜率k的取值范围.
19．函数f(x)的定义域为R，并满足以下条件：① 对任意x∈R，有f(x)>0； ② 对任意x，y∈R，有f(xy)=[f(x)]y； ③ f(
)>1.
（I）求f(0)的值；
（II）求证：f(x)在R上是单调增函数；
（III）若a>b>c>0，且b2=ac，求证：f(a)+f(c)>2f(b).
20．设函数f(x)的定义域、值域均为R，f(x)的反函数为
，且对于任意实数x，均有
，定义数列{an}：a0=8，a1=10，an=f(an－1)，n=1，2，…….
（I）求证：
；
（II）设bn=an+1－2an，n=0，1，2，……，求证：
（n∈N*）；
（III）是否存在常数A和B，同时满足：① 当n=0及n=1时，有
；② 当n=2，3，…….时，有
成立，
如果存在满足上述条件的实数A、B，求出A、B的值；如果不存在，证明你的结论。
北京市海淀区高三年级第二学期期末练习
数学（理科）答案
一、选择题（本大题共8小题，每小题5分，共40分）
1．C 2．D 3．A 4．C 5．D 6．C 7．B 8．C
二、填空题（本大题共6小题，每小题5分，共30分）
9．
10．0.98 11．
（2分） 
（3分） 12．
13．
（丢－6扣1分） 14．9（2分） 15（3分）
三、解答题（本大题共6小题，共80分）
15．（共13分） 解：（1）由m//n得
………………2分
即
………………4分
舍去 
………………6分
（2）
由正弦定理，
………………8分
………………10分
………………13分
16．（共14分）
解：（1）∵A1B1C1－ABC为直三棱住 ∴CC1⊥底面ABC ∴CC1⊥BC
∵AC⊥CB ∴BC⊥平面A1C1CA………………2分
∴BC长度即为B点到平面A1C1CA的距离
∵BC=2 ∴点B到平面A1C1CA的距离为2……………………4分
（2）分别延长AC，A1D交于G. 过C作CM⊥A1G 于M，连结BM
∵BC⊥平面ACC1A1 ∴CM为BM在平面A1C1CA的内射影
∴BM⊥A1G ∴∠GMB为二面角B—A1D—A的平面角 ……………………6分
平面A1C1CA中，C1C=CA=2，D为C1C的中点
∴CG=2，DC=1 在直角三角形CDG中， 
……8分
即二面角B—A1D—A的大小为
………………9分
（3）在线段AC上存在一点F，使得EF⊥平面A1BD ………………10分
其位置为AC中点，证明如下 ………………11分
∵A1B1C1—ABC为直三棱柱 ∴B1C1//BC
∵由（1）BC⊥平面A1C1CA，∴B1C1⊥平面A1C1CA
∵EF在平面A1C1CA内的射影为C1F ∵F为AC中点 ∴C1F⊥A1D ∴EF⊥A1D ………13分
同理可证EF⊥BD ∴EF⊥平面A1BD …………………14分
|
解法二：
（1）同解法一……………………4分
（2）∵A1B1C1—ABC为直三棱住 C1C=CB=CA=2
AC⊥CB D、E分别为C1C、B1C1的中点
建立如图所示的坐标系得
C（0，0，0） B（2，0，0） A（0，2，0）
C1（0，0，2） B1（2，0，2） A1（0，2，2）
D（0，0，1） E（1，0，2）………………6分
设平面A1BD的法向量为n
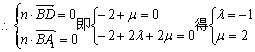
…………8分
平面ACC1A1的法向量为m=（1，0，0） 
…………9分
即二面角B—A1D—A的大小为
………………10分
（3）在线段AC上存在一点F，设F（0，y，0）使得EF⊥平面A1BD……11分
欲使EF⊥平面A1BD 由（2）知，当且仅当n//
…………12分
………………13分 ∴存在唯一一点F（0，1，0）满足条件
即点F为AC中点………………14分
17．（共13分）
解：（1）
………………2分
由已知条件得：
………………4分
（2）
………………5分
………………6分
令
………………7分
∴函数
的单调递增区间为
当
时，函数的单调递增区间为（0，2）…………8分
综上：当m>0时，函数的单调递增区间为；当时，
函数的单调递增区间为（0，2）………………9分
（3）由（1）得：
…………10分
令
………………11分
即：
……………………13分
18．（共13分）
解：（1）以FG的中点O为原点，以EF所在直线为y
轴，建立平面直角坐标系xoy，设点P（x，y）
|
…………2分
…………3分
…………4分
即所求点P轨迹方程
…………5分
（2）设点
设AF的斜率为
，BF的斜率为
，直线
的方程为
由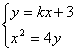
…………6分 
…………7分 
…………8分
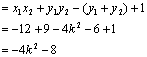
…………10分
由于
…………11分
解得
…………13分
∴直线斜率k的取值范围是
19．（共14分）解法一：（1）令
，得：
……………1分
…………………………3分
（2）任取
、
，且
. 设
则
……………………4分
在R上是单调增函数……10分
（3）由（1）（2）知
……………………11分
而
……………………14分
解法二：（1）∵对任意x、y∈R，有
………1分 ∴当
时
……2分
∵任意x∈R， 
……………………3分 
……………………4分
（2）
………………6分
是R上单调增函数 即是R上单调增函数；………………10分
（3）
……………………11分
而
……………………14分
20．（共13分）
（1）证明：
…………2分
即
…………4分
（2）证明：
…………6分
…………8分
（3）解：由（2）可知：
…………9分
假设存在常数A和B，使得
成立，则
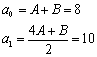解得A=B=4…………11分
下面用数学归纳法证明
成立.
（1）当n=2时，由
得
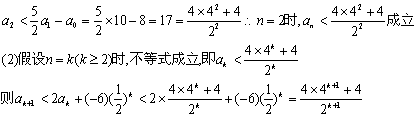
这说明
时，不等式成立.
综合（1）（2），可知
成立.…………13分
∴A=B=4满足题设. 说明：其它正确解法按相应步骤给分.