南昌十六中2005-2006年高三周练卷（13）

一、　　　　　　 选择题:（本题每小题5分，共60分）

1.的值是　　　　　　　　　　　　　　　　　　　　　　　　 

A．　　　　B．　　　　　  C．　　　　　　  D．

2．若的图象与的图象关于直线对称，则

　　　 A．　 B．　 C．　 D．

3．已知等差数列的前n项和为，若等于　　　　　　　　　　　　　

　　　 A．18　　　　　　　　　　　B．36　　　　　　　　　　　 C．54　　　　　　　　　　　D．72

4．已知函数的定义域为A，函数的定义域为B，则 　　　　　　A．　　 B．　　　　 C．A=B　　　　　　　　　 D．

5. 数列的前n项和, 则等于　(　 )　　　

A. 151　　 　　　B.　161　　　　　　 C.　171 　　　　　 D.　181

6. 中心在原点，准线方程为，离心率为的椭圆方程是（　　）　　　　　　　　　　　

　　　 A．　　　 B．　　　 C．　　　D．

7.将棱长为1的正方体木块削成一个体积最大的球，则该球的体积为（　　）　　　　

　　　 A．　　　　　　　　 B．　　　　　　　　 C．　　　　　　　　　 D．

8．设S_n是等差数列的前n项和，若（　）　

A．1　　　 　　　　　 B．－1　　 　　　　C．2　　　 　　　　　 D．

9．等差数列中，，，则此数列前20项和等（　　）

A．160　　　　　　　　　　　　　B．180　　　　　　　　　　C．200　　　　　　　　　　　D．220

10．数列的通项公式是，若前n项和为10，则项数n（　　）

A．11　　　　　　　　　　　　　　B．99　　　　　　　　　　　C．120　　　　　　　　　　　D．121

11．已知方程的四根组成一个首项为的等差数列,则等于（　）

A．1　　 B．　　　 C．　　　 D．

12．已知f(x)=bx+1为x的一次函数,　b为不等于1的常数, 且g(n)=,

设a_n= g(n)－g(n-1) (n∈N^※), 则数列｛a_n｝是（　）

　　 A 等差数列　　 B等比数列　　C　递增数列　　D　递减数列

二、填空题：（本大题每小题4分，共16分）

13. 记数列的前n项和为S_n，若，则数列的通项___________．

14、已知偶函数f (x)在[0, π)上是递减函数，那么下列三个数f (lg), f (), f()，

　　从大到小的顺序是_________.

15、等差数列｛a_n｝的前m项和为30, 前2m项和为100, 则它的前3m项和为　　　　　  .

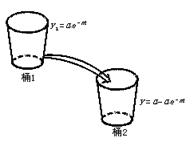
16、如图，开始时，桶1中有a L水，t分钟后剩余的水符合指数衰减曲线y=ae^－nt,那么桶2中水就是y₂=a－ae^－nt,假设过5分钟时，桶1和桶2的水相等，则再过_________分钟桶1中的水只有.

三、解答题：（本大题共6小题，共74分）

17、已知等差数列，数列，

（1）求的通项公式；

（2）令，求数列的前n项和S_n．

18．已知函数y＝2x²－2ax＋3在区间[－1, 1]上的最小值是f (a)，

(1)　  求函数f (a)的解析表达式；

(2)　  求函数g(a)＝logf (a)的单调区间。

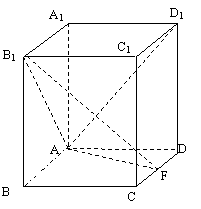
19．在棱长AB=AD=2，AA'=3的长方体中，点E是平面上动点，点F是CD的中点。

　（1）求直线到面的距离；

(2)求二面角－AF－B的大小；

（3）试确定E的位置，使⊥平面。

20. 已知向量且

求的值

21．数列满足，求

22. 已知函数f(x)= (x<－2).

(1)求f(x)的反函数f^-－1(x);

(2)设a₁=1, =－f^－-1(a_n)(n∈N^*),求a_n;

(3)设S_n=a₁²+a₂²+…+a_n²,b_n=S_n+1－S_n是否存在最小正整数m,使得对任意n∈N^*,有b_n<成立？若存在，求出m的值；若不存在，说明理由.

南昌十六中2006届高三数学周考试卷（13）　 　　　　　　　　　　 考试时间：2005-12-22　

　　　　　　　　　　

题号	一	二	三						总分
得分			17	18	19	20	21	22

一、选择题答题表：

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案

二、填空题答题表：

　　13、　　　　　　　　　 　　 14、　　　　　　　　　 　

15、　　　　　　　　　 　　 16、　　　　　　　　　 　

三、解答题（本题17—21小题每题12分，22小题14分，共74分）

17、(本小题满分12分)

18、(本小题满分12分)

19、(本小题满分12分)

20、(本小题满分12分)

21、(本小题满分12分)

22、(本小题满分14分)

参考答案及部分解答

一、选择题（每小题5分，共60分）：

1	2	3	4	5	6	7	8	9	10	11	12
A	A	D	D	B	D	C	A	B	C	C	B

二、填空题（每小题4分，共16分）

13.　　 14. f ()>f (lg)>f()。15、210

16、由题意，5分钟后，y₁=ae^－nt,y₂=a－ae^－nt,y₁=y₂.∴n=ln2.设再过t分钟桶1中的水只有,则y₁=ae^－n(5+t)=,解得t=10.

三、解答题（共74分，按步骤得分）

（18）解：(1) y＝2(x－)²＋3－, 当a<－2时, y在区间[－1, 1]上递增，最小值为f (－1)＝2a＋5;　 当a>2时, y在区间[－1, 1]上递减，最小值为f (1)＝－2a＋5;

　当－2≤a≤2时, y在区间[－1, 1]上的最小值为3－；

　∴f (a)＝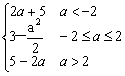　

　(2)  f (a)>0, 当－<a<－2时, 2a＋5为递增，f (a)为递减；

　当2<a<时, 5－2a为递减，f (a)为递增；

 当－2≤a<0时, 3－为递增，f (a)为递减； 当0<a≤2时, 3－为递减，f (a)为递增。

22 (1)设y=,∵x<－2,∴x=－,

即y=f^－-1(x)=－ (x>0)

(2)∵，

∴{}是公差为4的等差数列，

∵a₁=1, =+4(n－1)=4n－3,∵a_n>0,∴a_n=.

(3)b_n=S_n+1－S_n=a_n+1²=,由b_n<,得m>,

设g(n)= ,∵g(n)= 在n∈N^*上是减函数，

∴g(n)的最大值是g(1)=5,∴m>5,存在最小正整数m=6,使对任意n∈N^*有b_n<成立.

21.

　　 当时　∵ 　　　 ①

　　　　　　　　　 　②

　　 ①－②得　 ∴

　　 当时　上式

　　 ∴　.