南昌十六中2005-2006年高三周练卷（14）
一、 选择题:（本题每小题5分，共60分）
1. 设集合A和集合B都是实数集R，映射f：
把集合A中的元素x映射到集合B中元素：x3－x＋2，则在映射f下，象2的原象所成的集合是
A．{1} B．{0，1，－1} C．{0 } D．{0，－1，－2}
2．复数
的值是（ ）.
A. －1 B. 1 C. －32 D. 32
3．在
中，
，
，则该数列中相邻两项的乘积是负数的项是（ ）
A．
和
B．和
C．和
D．和
4．计算机是将信息转换成二进制进行处理的,二进制即“逢2进1”, 如(1101)2表示二进制数,将它转成十进制形式是1×23+1×22+0×21+1×20=13,那么将二进制数
转换成十进制形式是 ( )
A. 217－2 B. 216－2 C. 216－1 D. 215－1
5. 已知lg3, lg(sinx
), lg(1－y)顺次成等差数列,则
( )
A. y有最大值1, 无最小值 B. y有最小值－1, 最大值1
C. y有最小值
, 最大值1 D. y有最小值, 无最大值
6. 已知数列
的前n项和
，那么下述结论正确的是（ ）
A．
为任意实数时，是等比数列 B．= －1时，是等比数列
C．=0时，是等比数列 D．不可能是等比数列
7. 数列{an}满足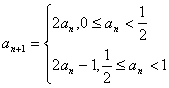
, 若
, 则a2005的值为 ( )
A. 
B.
C.
D.
8．已知过球面上A、B、C三点的截面和球心的距离等于球半径的一半，且AB=BC=CA=2，则球面面积为
A．
B．
C．4π D．
9．双曲线
离心率为2，有一个焦点与抛物线
的焦点重合，则mn的值为（ ）
A．
B．
C．
D．
10．设函数
满足
，且
，则
（ ）
A．95 B．97 C．105 D．192
11．已知点A为双曲线
的左顶点，点B和点C在双曲线的右支上，
是等边三角形，则的面积是（ ）
A． 
B．
C．
D．
12．某工厂2004年生产某产品2万件，计划从2005年开始，每年的产量比上一年增长20%，经过n年这家工厂生产这种产品的年产量超过12万件。则n的值为（ ）
（已知lg2=0.3010,lg3=0.4771）
A．11 B．12 C．13 D．14
二、填空题：（本大题每小题4分，共16分）
13、
数列的前ｎ项的和Sn =3n2+ n+1，则此数列的通项公式a n=_______.
14、已知
的夹角为θ,且
,则cos
的值为____________
15、设F1，F2是椭圆
的两个焦点，P是椭圆上的点，且PF1 : PF2＝2 : 1，则三角形
PF1F2的面积等于______________．
16、若数列
满足
，且
，则
的值为______________。
三、解答题：（本大题共6小题，共74分）
17、已知：等差数列{
}中，
=14，前10项和
.
（Ⅰ）求；
（Ⅱ）将{}中的第2项，第4项，…，第
项按原来的顺序排成一个新数列，求此数列的前
项和
.
18． （1）已知
=4，
=3，（2－3）·（2+）=61，求与的夹角θ；
（2）设
=（2，5），
=（3，1），
=（6，3），在上是否存在点M，使
，若存在，求出点M的坐标，若不存在，请说明理由.
19．已知向量
（Ⅰ）求
的值；
（Ⅱ）若
的值
20. 设Sn为数列{an}的前ｎ项的和，且Sn =
(an －1)(n∈N*)， 数列{bn }的通项公式
bn = 4n+5. ①求证：数列{an }是等比数列；
②若d∈{a1 ，a2 ，a3 ，……}∩{b1 ，b2 ，b3 ，……}，则称d为数列{an }和{bn }的公共项，按它们在原数列中的先后顺序排成一个新的数列{dn }，求数列{dn }的通项公式.
21．已知函数f (x) 和g
(x)的图象关于原点对称，且f (x) =x
+2x.
( 1 ) 求函数g (x) 的解析式
（2）解不等式g (x) ≥ f (x) -︱x-1︱
（3）若h(x)=g
(x) -
f (x)+1在〔-1，1〕上是增函数，求实数的取值范围。
22. 已知函数
。
（Ⅰ）求f（x）的反函数，并指出其定义域；
（Ⅱ）设数列
的前n项和为
，若对于所有大于1的自然数n都有
，且
，求数列的通项公式；
（Ⅲ）令
，求：
南昌十六中2006届高三数学周考试卷（14） 考试时间：2005-12-29
| 题号 | 一 | 二 | 三 | 总分 | |||||
| 得分 | 17 | 18 | 19 | 20 | 21 | 22 | |||
|
|
|
|
|
|
| ||||
一、选择题答题表：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题答题表：
13、 14、
15、 16、
三、解答题（本题17—21小题每题12分，22小题14分，共74分）
17、(本小题满分12分)
18、(本小题满分12分)
19、(本小题满分12分)
20、(本小题满分12分)
21、(本小题满分12分)
22、(本小题满分14分)
参考答案及部分解答
一、选择题（每小题5分，共60分）：
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| B | A | C | C | D | B | A | D | A | B | C | A |
二、填空题（每小题4分，共16分）
13. 
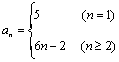14. 
15、4 16、102
三、解答题（共74分，按步骤得分）
17、（Ⅰ）由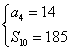
∴ 
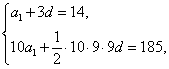
……3分
由
……………………………6分
（Ⅱ）设新数列为{
}，由已知，
………………… 9分
……………………………………12分
18．解：（1）∵（2－3）·（2+）=61，∴
又=4，=3，∴·=－6.
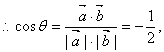
∴θ=120°.
（2）设存在点M，且
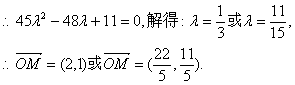
∴存在M（2，1）或
满足题意.
19.（1）
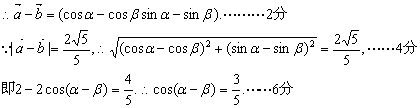
（2）
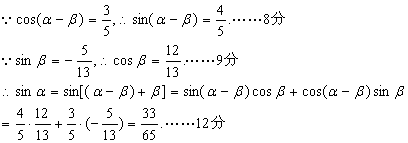
20、分析：①利用公式an=Sn－Sn－1代入得出an与an－1之间的关系.②令ak=bm ，再找出k，m之间的联系.
解：①当n=1时，由a1=S1=
，得出a1=3.当n≥2时，
………6分
②由an=3n，得：
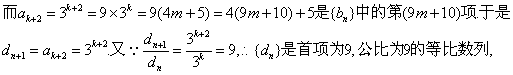
因此dn=9×9n—1、=9n. ……………………………………………………12分
评注：本题中的①，由Sn和Sn—1作两式相减，这是处理类似的关系式的重要的方法，特别是对于an+1=pan+q（p，q为常数）也是有效的.②的解法提供了一种求公共项的方法，若两个数列都是等差数列，则它们的公共项也为等差数列，公差为它们的最小公倍数.若都为等比数列，请读者思考公共项是否仍为等比数列
21．解：（1）设函数y= f (x)的图像上任一点Q(x
，y )关于原点的对称点为P（x, y）则 
即 x=-x
y=-y
∵点Q（x,y）在函数y= f (x)的图像上，∴-y = x-2 x,即y = - x+ 2 x , 故g (x) = - x+ 2 x.
(2)由g (x) ≥ f (x)－︱x -1︱可得 , 2 x- ︱x - 1︱≤0
当x ≥1时, 2 x- x + 1 ≤0, 此时不等式无解.
当x ＜1时, 2 x+ x – 1 ≤0 , ∴ - 1 ≤ x ≤
原不等式的解集为［ -1, ］
(3) h(x) =-( 1+λ)x+ 2(1-λ) x + 1
①当λ=-1时, h(x) = 4x+1在［-1,1］上是增函数, ∴λ = - 1
②当λ≠-1时 ,对称轴的方程为 x =
.
(i)当λ＜- 1时, ≤- 1, 解得λ＜ - 1
(ii)当λ＞- 1时, ≥ 1, 解得 - 1＜λ≤ 0. 综上, λ ≤ 0.
22解：（I）设y = f (x)，
，（x≥0）。
……………………………………………………………………………………………2分
∵x ≥0， ∴y ≥2.
∴
. ∴
.
∴f (x) 的反函数为
，（x≥2）.…………………………4分
（II）∵
，，
∴
，
.
即
.
数列
是等差数列，公差为
，
.
∴
.
即
（n∈N）.……………………………………………………8分
当n≥2时，
，
当n = 1时，，满足
∴（n∈N）.………………………………………………10分
（III）∵
，
∴
.
……………………………………………………………………………12分
∴
.………………………………14分