南昌十六中2005-2006年高三周练卷(15)
一、 选择题:(本题每小题5分,共60分)
1.已知集合A =![]() ,且B
,且B![]() A,则集合B的个数为
( )
A,则集合B的个数为
( )
A. 3个 B. 4个 C. 8个 D.16个
2.如果![]() ,则下式正确的是
(
)
,则下式正确的是
(
)
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3、关于x的不等式![]() 的解集为(1,+∞),则关于x的不等式
的解集为(1,+∞),则关于x的不等式![]() >0的
>0的
解集为 ( )
A.(-1,2) B.(1,2) C.(-∞,-1)∪(2,+∞) D.(―∞,―2)∪(1,+∞)
4、等差数列![]() 各项都为正数,且
各项都为正数,且![]() .则此数列前
.则此数列前
12 项之和为 ( )
A.16 B.24 C.48 D.64
5、若关于![]() 的方程
的方程![]() 有一根为1,则
有一根为1,则![]() 中一定有
中一定有
A.![]() B.
B.
![]() C.
C.![]() D.
D.![]() 。
。
6、已知![]() ,则向量
,则向量![]() 与向量
与向量![]() 的夹角是 ( )
的夹角是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
7、已知函数![]() 则
则![]() 的大小关系为( )
的大小关系为( )
A. ![]() B.
B. ![]()
C.![]() D.
D.![]()
8、将函数![]() 的图象按向量
的图象按向量![]() (其中,
(其中,![]() )平移后
)平移后
与![]() 的图象重合,则向量
的图象重合,则向量![]() 坐标为 ( )
坐标为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9、已知数列{an},如果a1,a2-a1,a3-a2,…,an-an-1,…,是首项为1,公比为的等比数列,则an=( )
A.(1-) B.(1-) C.(1-) D.(1-)
10、在等差数列![]() 中,a1=1,a7=4,数列
中,a1=1,a7=4,数列![]() 是等比数列,已知b2=a3,b3=
是等比数列,已知b2=a3,b3=![]() ,则满足
,则满足
bn<![]() 的最小自然数n是 ( )
的最小自然数n是 ( )
A.8 B.7 C.6 D.5
11、定义运算:![]() ,若数列
,若数列![]() 满足
满足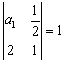 ,且
,且![]() (
(![]() ),则
),则![]() 为( )
为( )
A.34 B.36 C.38 D.40
12、设![]() 是定义在
是定义在![]() 上恒不为零的函数,对任意实数
上恒不为零的函数,对任意实数![]() 皆有
皆有![]() ,若
,若![]() ,则数列
,则数列![]() 前
前![]() 项和
项和![]() 的取值范围是
( )
的取值范围是
( )
A.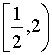 B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题:(本大题每小题4分,共16分)
13、等差数列{an}中,a1=,前n项和为Sn,且S3=S12.则a8= .
14、已知![]() .
.
15、![]() ,则
,则![]() =_____________.
=_____________.
16、定义“等和数列”:在一个数列中,如果每一项与它的后一项的和都为同一个常数,那么这个数列叫做等和数列,这个常数叫做该数列的公和。
已知数列![]() 是等和数列,且
是等和数列,且![]() ,公和为5,那么这个数列的前21项和
,公和为5,那么这个数列的前21项和![]() 的值为__ 。
的值为__ 。
三、解答题:(本大题共6小题,共74分)
17、已知![]() ,
,![]() (
(![]() ),
),
(1)求![]() 关于
关于![]() 的表达式,并求
的表达式,并求![]() 的最小正周期;
的最小正周期;
(2)若![]() ,且
,且![]() 的最小值为5,求
的最小值为5,求![]() 的值.
的值.
18.设![]() 为公差大于0的等差数列,
为公差大于0的等差数列,![]() 为数列
为数列![]() 的前n项的和. 已知S4=24,
的前n项的和. 已知S4=24,
![]()
(1)求数列![]() 的通项公式
的通项公式![]() (2)若
(2)若![]() 的前n项和Tn.
的前n项和Tn.
19.数列{an}的前n项和为![]() 若将此数列按如下规律编组:
若将此数列按如下规律编组:
(a1), (a2, a3), (a4, a5, a6)……,(1)求:数列{an}的通项公式。(2)求第n组的n个数之和。
20. 已知![]() 成等差数列(n为正偶数).又
成等差数列(n为正偶数).又![]() (1)求:数列{an}的通项公式。(2)
(1)求:数列{an}的通项公式。(2)![]() 的3的大小。
的3的大小。
21.设双曲线![]() 的焦点分别为F1、F2,离心率为2
的焦点分别为F1、F2,离心率为2
(Ⅰ)求此双曲线的渐近线L1、L2的方程。
(Ⅱ)若A、B分别为L1、L2的动点,且2│AB│=5│F1F2│。求线段AB的中点M的轨迹方程。并说明轨迹是什么曲线?
22. 已知函数![]()
(Ⅰ)用![]() 表示
表示![]()
(Ⅱ)求数列![]() 的通项公式;
的通项公式;
(Ⅲ)令![]() ,求数列
,求数列![]() 的最大项和最小项
的最大项和最小项
南昌十六中2006届高三数学周考试卷(15) 考试时间:2006-01-05
![]()
| 题号 | 一 | 二 | 三 | 总分 | |||||
| 得分 | 17 | 18 | 19 | 20 | 21 | 22 | |||
|
|
|
|
|
|
| ||||
一、选择题答题表:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题答题表:
13、 14、
15、 16、
三、解答题(本题17—21小题每题12分,22小题14分,共74分)
17、(本小题满分12分)
周练(15)参考答案及部分解答
一、选择题(每小题5分,共60分):
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| C | A | A | C | B | B | A | D | A | B | C | C |
二、填空题(每小题4分,共16分)
13. 13. 0 14.![]() 15、
15、![]() 16、52
16、52
三、解答题(共74分,按步骤得分)
17、解:(1)![]()
![]()
![]() 的最小正周期是
的最小正周期是![]() ……(6分)
……(6分)
(2)![]() ,
, ![]()
![]()
![]() 的最小值是
的最小值是![]()
![]() ……(12分)
……(12分)
18.解:(1)![]() (2分)
(2分)
由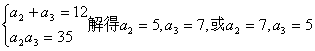 (4分)
(4分)
![]() (6分)
(6分)
![]() (8分)
(8分)
(2)![]() (10分)
(10分)
![]() (12分)
(12分)
19.(1)![]()
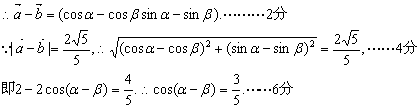
(2)![]()
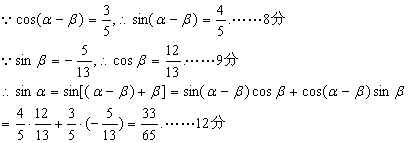
19、解:由![]()
由于n=1也成立,![]() 分组是(5),(9,13),(17,21,25),……,
分组是(5),(9,13),(17,21,25),……,
设{an}:5,9,13,…,所求第n组中n个数的和应为
![]()
![]()
20设等差数列{an}的公差为d,及f(1)=n2,f(-1)=n,得![]()
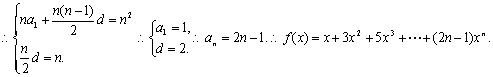
![]()
二式相减得:![]()
![]()