南昌十六中2005-2006年高三周练卷（16）
一、 选择题:（本题每小题5分，共60分）
1、已知
（ ）
A．
B．（
） C．
D．（
）
2、
（ ）
A．
B．
C．
D．
３、已知平面上三点A、B、C满足
，
，
，则
的值等于 （ ）
A．25 B．24 C．－25 D．－24
４、设a，b，c是空间三条直线，
，
是空间两个平面，则下列命题中，逆命题不成立的是（ ）
A．当c⊥时，若c⊥，则∥ B．当
时，若b⊥，则
C．当，且c是a在内的射影时，若b⊥c，则a⊥b
D．当，且
时，若c∥，则b∥c
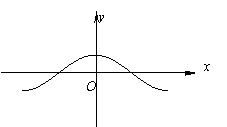
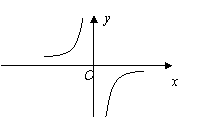5、函数y=f(x)与y=g(x)的图象如下图：
则函数y=f(x)g(x)的图象可能为（ ）
A B C D
6、 
（ ）
A.等腰三角形 B. 直角三角形 C.等腰直角三角形 D.等腰三角形或直角三角形7、 若(x
–
)6的展开式中的第五项是
, 设Sn = x –1
+ x –2 + … + x –
n , 则
Sn等于
（ ）
A．1 B． 
C． 
D．
8、设双曲线
的一条准线方程为
，则k的值为 （ ）
A．
B．
C．
D．
9、将函数
的图象按向量a
平移，得到
的图象，那么函数
可以是（ ）
A．
B．
C．
D．
10、已知函数
在区间
上是增函数，则实数
的取值范围是（ ）A．
B．
C．
∪ D．
11、将3种农作物都种植在如图的4块试验田里，
每块种植一种农作物，要求相邻的试验田不能
种植同一种作物，则不同的种植方法共有（ ）
A．6种 B．12种 C．18种 D．24种
12、现有一块正三棱锥形石料，其三条侧棱两两互相垂直，且侧棱长为1m，若要将这块石料打磨成一个石球，则所得石球的最大半径约为（ ）
A．0.18m B．0.21m C．0.24m D．0.29m
二、填空题：（本大题每小题4分，共16分）
13、已知直线
的方程为
，若直线
上有相异两点关于直线
对称，则
的值为 ．
14、已知
，
，且
，则
．
15在数列
在直线
上，
，则
。
16、在正方体
中，
与
交于点
，点
在线段
上运动，异面直线
与
所成的角为
，则的取值范围是 ．
三、解答题：（本大题共6小题，共74分）
17、已知f (x ) = 2cos2x +2
sinx cosx + a (a为常数)
（1）求f (x)的最小正周期 （2）求f (x)的单调递增区间
（3）若f (x)在[
, 
]上最大值与最小值之和为3，求a的值.
18、已知向量
，
，其中O为坐标原点．
（1）若
，求向量
与
的夹角；
（2）若
≥
对任意实数
都成立，求实数
的取值范围．
19、在直三棱柱
中，
，
,
分别是
，
的中点，点
在
上，且
．
（1）求证:
；（2）求二面角
的正切值．
（3）求点
到平面EFG的距离．
20、已知函数f (x) = a·bx的图像过点A（1, 
）, B (2 , 
)
(1 ) 求函数f ( x ) 的解析式.
（2）设
, n∈N+, Sn 是数列
前n项和，求S20.
（3）在(2 )的条件下，若 
，求数列{bn}的前n项和Tn.
21、设
、
，
、
为直角坐标平面内、轴正方向上的单位向量，若向量
且
求点
的轨迹
的方程
过点
作直线与曲线交于
、
两点，设
。是否存在这样的直线
，使得四边形
是矩形？若存在，求出直线的方程；若不存在，说明理由。
22. 已知函数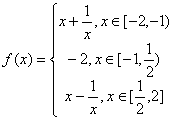
（I）
求
的值域；
（II）设函数
，若对于任意
总存在
，使得
成立，求实数
的取值范围。
南昌十六中2006届高三数学周考试卷（16）
| 题号 | 一 | 二 | 三 | 总分 | |||||
| 得分 | 17 | 18 | 19 | 20 | 21 | 22 | |||
|
|
|
|
|
|
| ||||
一、选择题答题表：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题答题表：
13、 14、
15、 16、
三、解答题（本题17—21小题每题12分，22小题14分，共74分）
17、(本小题满分12分)
18、(本小题满分12分)
19、(本小题满分12分)
周练（16）参考答案及部分解答
一、选择题（每小题5分，共60分）：
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| A | B | C | B | A | D | A | B | D | A | C | B |
二、填空题（每小题4分，共16分）
13．
14．
15、2 16、[ ，
]
三、解答题（共74分，按步骤得分）
17.解：f (x) =sin2 x + cos2 x + a + 1 = 2sin (2 x +) + a +1……………………（2分）
（1）T = π…………………………………………………………………………… (4分)
（2）由2kπ－
≤2x +≤2 kπ+ 得kπ－≤x≤kπ+
f (x)单调递增区间为[kπ－ , kπ+] (k∈ z ) ……………………………（8分）
（3）由（2）知f (x)在[－ ，]为增函数
f () + f (－) = 3
a = 0 ……………………………………………………………………………（12分）
18、（1）设向量
与
的夹角为
，
则
， ……………2分
当
时，
，
； ……………………………4分
当
时，
，
．
故当时，向量与的夹角为
；
当时，向量与的夹角为
． ……………………………6分
（另法提示：
，它可由向量
绕O点逆时针旋转而得到，然后分
和
进行讨论．）
（2）
对任意的
恒成立，
即
对任意的恒成立，
即
对任意的恒成立，
……………………………8分
所以，
或
，
……………………………10分
解得
或
．
故所求实数
的取值范围是
∪
． ……………………………12分
（另法一提示：由对任意的恒成立，可得
，解得
或
，由此求得实数的取值范围；
另法二提示：由
，可得
的最小值为
，然后将已知条件转化为
，由此解得实数的取值范围）
19、1）因图像过点A（1，）, B（2, ）
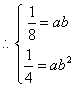
解之得 a = 
, b = 2 …………………………………………………………(2分)
f (x) == 
……………………………………………………… (4分)（2）
是首项为－3公差为1的等差数列………………………………………（6分）
Sn = －3n+
= 
n (n－7)
= 130 …………………………………………………………………(8分)
（3）
Tn = －3·+ (－2)· ()2 + …… + (n－ 4) () n
…………①
Tn = (－3)· ()2 + …… + (n－5) () n + (n－4 ) ()n+1
……②
①－②得：Tn = －3·+ ()2 + …… + ()n－(n－4) ()n+1
Tn = －2－ (n－2) ()n ………………………………………………… (12分)
20．解：（1）连结
，
，
∵
分别是
的中点，
∴
∥，且
．
在直三棱柱中，由
可知侧面
是正方形，∴
．……２分
∵
，
，∴
平面
，
∴
在平面上的射影是
，
由三垂线定理可得
，
∴.
……………………………………………………4分
（2）取
的中点
，连结
，则
平面
．
作
于点
，连结
，由三垂线定理可知
，
∴
为二面角
的平面角，
……………………………6分
易知Rt
∽Rt
，∴
， ……………………………7分
在Rt
中，求得
，
∴所求二面角
的正切值为
．
……………………………9分
（3）在Rt中，作
于点
，
由（2）可知，
平面
，
∴
，∴
平面
，
的长是点到平面的距离．
在Rt
中，
，
……………………………12分
又
，点
是的中点，
∴点
到平面的距离为
．
……………………………14分
（另法提示：利用体积法，由
求解．）
解法二：（1）建立如图的空间直角坐标系O -xyz，则
，
，
，
∴
，
，
…………………………………………2分
∵
·
，
∴⊥
，即
．…………………4分
（2）设n= (x,y,1)是平面EFG的一个法向量，
则有n⊥, n ⊥
,∴n ·=0, n ·=0,
即
,且
,
解得
,故n= (
,1)． ………6分
易知向量m =
是侧面
的一个法向量．
设向量m与向量n的夹角为，
则
，∴
， ……………………………………8分
而二面角的平面角大于直角，
所以二面角的平面角与互补．故所求二面角的正切值为
．……9分
（3）设点到平面EFG的距离为d，则d等于向量
在向量n上的投影，…………11分
即d=()·
·
．
故点到平面EFG的距离为
． ………………14分
21、解：⑴ 设
所以点
的轨迹是以
为焦点的椭圆，其方程为：
⑵设存在这样的直线 椭圆交于
，
ⅰ.当直线的倾斜角为
时，经检验，不合题意
ⅱ.当直线的斜率存在时，设直线方程为：
与椭圆方程
联立得：
又由题意知：
解得 
存在这样的直线：
，使得四边形是矩形
解：（I）当
时，
在
上是增函数，此时
当
时，
当
时，
在
上是增函数，此时
的值域为
……………………………6 分
（II）（1）若
，
对于任意
，
，不存在 使得 成立
（2）若当
时， 
在[-2，2]是增函数，
任给，，
若存在，使得成立，
则
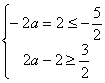
……………………………………10分
（3）若
，在[-2，2]是减函数，
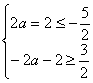
综上，实数的取值范围是
………………………………14