南昌十六中2005-2006年高三周练卷(17)
一、 选择题:(本题每小题5分,共60分)
1.已知a>b>0,全集为R,集合![]() ,
,![]() ,
,![]() ,则有( )
,则有( )
A.![]() (
(![]()
![]() ) B.
) B.![]() (
(![]()
![]() )
)![]() C.
C.![]() D.
D.![]()
2.已知实数a,b均不为零,![]() ,且
,且![]() ,则
,则![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.已知函数![]() 的图像关于点(-1,0)对称,且当
的图像关于点(-1,0)对称,且当![]() (0,+∞)时,
(0,+∞)时,![]() ,则当
,则当![]() (-∞,-2)时
(-∞,-2)时![]() 的解析式为( )
的解析式为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.在坐标平面上,不等式组![]() 所表示的平面区域的面积为
( )
所表示的平面区域的面积为
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.二次函数f(x)满足f(3+x)=f(3-x),又f(x)是[0,3]上的增函数,且f(a)≥f(0),那么实数a的取值范围是( )
A. a≥0 B. a≤0 C. 0≤a≤6 D. a≤0或a≥6
6.函数![]() 的图象一个对称中心的坐标是 ( )
的图象一个对称中心的坐标是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.两个非零向量a,b互相垂直,给出下列各式:
①a·b=0; ②a+b=a-b; ③a+b=a-b; ④a![]() +b
+b![]() =
=![]() a+b
a+b![]() ;
;
⑤(a+b)·(a-b)=0.其中正确的式子有( )
A.2个 B.3个 C.4个 D.5个
8.已知数列![]() 的前n项和为
的前n项和为![]() ,
,![]() ,现从前m项:
,现从前m项:![]() ,
,![]() ,…,
,…,![]() 中抽出一项(不是
中抽出一项(不是![]() ,也不是
,也不是![]() ),余下各项的算术平均数为37,则抽出的是( )
),余下各项的算术平均数为37,则抽出的是( )
A.第6项 B.第8项 C.第12项 D.第15项
9.已知双曲线![]() (a>0,b>0)的两个焦点为
(a>0,b>0)的两个焦点为![]() 、
、![]() ,点A在双曲线第一象限的图象上,若△
,点A在双曲线第一象限的图象上,若△![]() 的面积为1,且
的面积为1,且![]() ,
,![]() ,则双曲线方程为( )
,则双曲线方程为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.函数y=sin2x+5sin(![]() +x)+3的最小值为( )
+x)+3的最小值为( )
A. -3 B. -6 C.![]() D. -1
D. -1
11.在正三棱锥A-BCD中,E,F分别是AB,BC的中点,EF⊥DE,且BC=1,则正三棱锥A-BCD的体积等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.已知![]() 是定义在R上的偶函数,且对任意
是定义在R上的偶函数,且对任意![]() ,都有
,都有![]() ,当
,当![]() [4,6]时,
[4,6]时,![]() ,则函数
,则函数![]() 在区间[-2,0]上的反函数
在区间[-2,0]上的反函数![]() 的值
的值![]() 为( )
为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题:(本大题每小题4分,共16分)
13.若实数a,b均不为零,且![]() ,则
,则![]() 展开式中的常数项等于________.
展开式中的常数项等于________.
14.复数![]() ,
,![]() ,则复数
,则复数![]() 的虚部等于_______ .
的虚部等于_______ .
15.函数![]() 的单调递减区间为
.
的单调递减区间为
.
16.给出下列4个命题:
①函数![]() 是奇函数的充要条件是m=0:
是奇函数的充要条件是m=0:
②若函数![]() 的定义域是
的定义域是![]() ,则
,则![]() ;
;
③若![]() ,则
,则![]() (其中
(其中![]() );
);
④圆:![]() 上任意点M关于直线
上任意点M关于直线![]() 的对称点,
的对称点,![]() 也在该圆上.
也在该圆上.
填上所有正确命题的序号是________.
三、解答题:(本大题共6小题,共74分)
17、已知![]() ,
,![]() (
(![]() ),
),
(1)求![]() 关于
关于![]() 的表达式,并求
的表达式,并求![]() 的最小正周期;
的最小正周期;
(2)若![]() ,且
,且![]() 的最小值为5,求
的最小值为5,求![]() 的值.
的值.
18、已知二次函数![]() 对任意
对任意![]() ,都有
,都有![]() 成立,设向量
成立,设向量![]() (sinx,2),
(sinx,2),![]() (2sinx,
(2sinx,![]() ),
),![]() (cos2x,1),
(cos2x,1),![]() (1,2),当
(1,2),当![]() [0,
[0,![]() ]时,求不等式f(
]时,求不等式f(![]() )>f(
)>f(![]() )的解集.
)的解集.
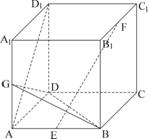
19、如图正方体在ABCD-A1B1C1D1中,E,F,G分别为AB,B1C1,AA1的中点,
(1) 求证:EF⊥平面GBD;
(2) 求异面直线AD1与EF所成的角 .
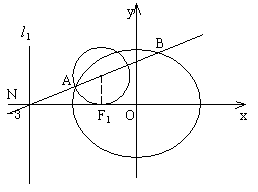
20、
![]()
![]()
![]()
![]()
![]()
圆中,求面积最小的圆的半径长。
21、已知非零向量![]() ,
,![]() ,
,![]() 满足
满足![]() ,记
,记![]() 与
与![]() 之间关系式为
之间关系式为![]() 。
。
(1)当![]() 时,求
时,求![]() 最小值;
最小值;
(2)设数列![]() 前
前![]() 项和
项和![]() ,且满足
,且满足![]() ,
,![]() ,求数列通项
,求数列通项![]() 。
。
22. 设![]() =
=![]() (a>0)为奇函数,且
(a>0)为奇函数,且
![]() min=
min=![]() ,数列{an}与{bn}满足 如下关系:a1=2,
,数列{an}与{bn}满足 如下关系:a1=2, ![]() ,
,![]() .
.
(1)求f(x)的解析表达式;
(2) 证明:当n∈N+时, 有bn![]()
![]() .
.
南昌十六中2006届高三数学周考试卷(17)
![]()
| 题号 | 一 | 二 | 三 | 总分 | |||||
| 得分 | 17 | 18 | 19 | 20 | 21 | 22 | |||
|
|
|
|
|
|
| ||||
一、选择题答题表:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题答题表:
13、 14、
15、 16、
三、解答题(本题17—21小题每题12分,22小题14分,共74分)
17、(本小题满分12分)
18、(本小题满分12分)
19、(本小题满分12分)
周练(17)参考答案及部分解答
一、选择题(每小题5分,共60分):
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| A | B | B | B | C | B | A | B | A | D | B | B |
二、填空题(每小题4分,共16分)
13. -672 14.![]() 15、(0,1) 16、①,④
15、(0,1) 16、①,④
三、解答题(共74分,按步骤得分)
17.解:(1)![]()
![]()
![]() 的最小正周期是
的最小正周期是![]() ……(6分)
……(6分)
(2)![]() ,
, ![]()
![]()
![]() 的最小值是
的最小值是![]()
![]() ……(12分)
……(12分)
18.解析:设f(x)的二次项系数为m,其图象上两点为(1-x,![]() )、B(1+x,
)、B(1+x,![]() )因为
)因为![]() ,
,![]() ,所以
,所以![]() ,由x的任意性得f(x)的图象关于直线x=1对称,若m>0,则x≥1时,f(x)是增函数,若m<0,则x≥1时,f(x)是减函数.
,由x的任意性得f(x)的图象关于直线x=1对称,若m>0,则x≥1时,f(x)是增函数,若m<0,则x≥1时,f(x)是减函数.
∵ ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,
∴ 当![]() 时,
时,![]()
![]()
![]()
![]()
![]()
![]() ,
,![]() .
.
∵ ![]() , ∴
, ∴ ![]() .
.
当![]() 时,同理可得
时,同理可得![]() 或
或![]() .
.
综上:![]() 的解集是当
的解集是当![]() 时,为
时,为![]() ;
;
当![]() 时,为
时,为![]() ,或
,或![]() .
.
19、异面直线AD1与EF所成的角为30º
20.![]() ………………1分
………………1分
![]()
![]() ………………3分
………………3分
![]() ………………4分
………………4分
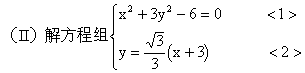
![]() …………6分
…………6分
![]()
![]() ………………7分
………………7分
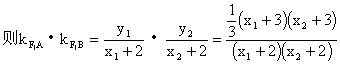
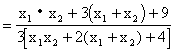
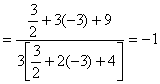 ………………11分
………………11分
![]()
![]() ………………12分
………………12分
(III)面积最小的圆的半径应是点F到直线l的距离,设为r………………13分
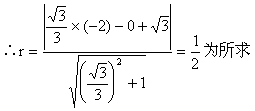 ………………14分
………………14分
21、①
![]()
![]() ,由
,由![]() 得,
得,
![]()
![]()
② ∵ ![]() ∴
∴ ![]()
∴ ![]() ∴
∴ ![]()
∴ ![]() 是以
是以![]() 为首项,1为公差的等差数列
为首项,1为公差的等差数列
∴ ![]() ∴
∴ ![]()
∴ ![]() (
(![]() )
)
∴ 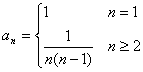
22.解:由f(x)是奇函数,得 b=c=0, (3分)
由f(x)min=![]() ,得a=2,故f(x)=
,得a=2,故f(x)= ![]() (6分)
(6分)
(2) ![]() =
=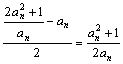 ,
,
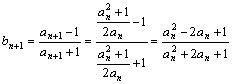 =
=![]() =
=![]() (8分)
(8分)
∴![]() =
=![]() =
=![]() =…=
=…=![]() ,而b1=
,而b1=![]()
∴![]() =
=![]() (10分)
(10分)
当n=1时, b1=![]() ,命题成立,
(12分)
,命题成立,
(12分)
当n≥2时
∵2n-1=(1+1)n-1=1+![]() ≥1+
≥1+![]() =n
=n
∴![]() <
<![]() ,即 bn≤
,即 bn≤![]() .
(14分)
.
(14分)
注:不讨论n=1的情况扣2分.