江苏省南师大附中2006年高考预测卷
数学试题 2006.05.25
第Ⅰ卷(选择题共50分)
一、选择题：每小题5分，共50分．
1．下列四个函数中，值域是(－∞，－2]的一个函数是 （ D ）
(A)y＝－2x＋1(x＞) (B)y＝－(x＋1)2－2(－1≤x≤0)
(C)y＝x＋(x＜－1) (D)y＝log0.5(x＋＋1)(x＞1)
2．某工人1天出废品的概率为0.2，工作4天，恰有2天出废品的概率为 ( A )
A．0.1536 B．0.0256 C．0.24 D．0.384
3．已知直线m，n和平面α，则m∥n的一个必要不充分条件是 ( D )
(A)m∥α，n∥α (B)m⊥α，n⊥α (C)m∥α，n
α (D)m，n与α所成角相等
４．已知向量a＝(2cosα，2sinα)，b＝(3cosβ，3sinβ)，a与b的夹角为60o，则直线xcosα－ysinα＋1＝0与圆(x－cosβ)2＋(y＋sinβ)2＝1的位置关系是 ( C )
(A)相切 (B)相交 (C)相离 (D)随α，β的值而定
５．已知x，y满足约束条件则z＝2x＋4y的最小值为 ( D )
(A)10 (B)－10 (C)6 (D)－6
６．进入21世纪，肉食品市场对家禽的需求量大增，发展家禽养殖业成了我国一些地区发展农村经济的一个新举措．下列两图是某县2000～2005年家禽养殖业发展规模的统计结果，那么，此县家禽养殖数最多的年份是 ( B )
 |
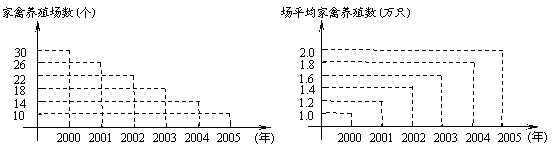(A)2000年 (B)2001年 (C)2003年 (D)2004年
７．已知椭圆＋＝1上有n个不同的点P1，P2，P3，…，Pn．设椭圆的右焦点为F，数列｛PnF｝是公差大于的等差数列，则n的最大值为 ( B )
(A)2007 (B)2006 (C)1004 (D)1003
８．用平面
截半径为R的球，如果球心到截面的距离为
，那么截得小圆的面积与球的表面积的比值为
( D )
A．1：3 B．3：4 C．4：3 D．3：16
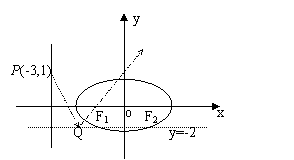9．点P（－3，1）在椭圆
的左准线上．过点P且方向向量为a＝(2，－5)的光线，经直线y＝－2反射后通过椭圆的左焦点，则这个椭圆的离心率为 ( A )
A． 
B．
C． 
D．
10．若
并且
，则实数对（m，n）表示平面上不同点的个数为 ( C )
A．60个 B．70个 C．90个 D．120个
第Ⅱ卷(非选择题共100分)
二、填空题：本大题共6小题；每小题5分，共30分．把答案填在题中横线上．
11．抛物线
的准线方程是________ x=－1 ____________________．
1２． 已知向量a
，b
，若
a -b与a垂直，实数等于
．
1３． 已知m≥2，n≥2且m、n为正整数，对m的n次幂进行如下方式的“分裂”，
仿此，以下几个关于“分裂”的叙述：
 |
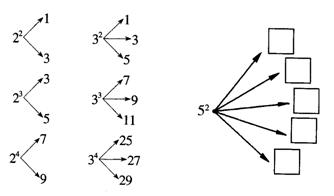（1）52 的“分裂”中最大的数是9；（2）44 的“分裂”中最小的数是13；（3）若m3的“分裂”中最小的数是211，则m的值为15。上述关于“分裂”的正确叙述的序号是（1）（3） 。（写出所有正确的叙述的序号）
１４．将一张画有直角坐标系的图纸折叠一次，使得点A(0，2)与点B(4，0)重合．若此时点C(7，3)与点D(m，n)重合，则m＋n的值是
１５．有下列命题：
①G＝（G≠0）是a，G，b成等比数列的充分非必要条件；
②若角α，β满足cosαcosβ=1，则sin(α+β)＝0；
③若不等式x－4+x－3＜a的解集非空，则必有a≥1；
④函数y=sinx+sinx的值域是［－2，2］．
其中正确命题的序号是①②④ ．（把你认为正确的命题的序号都填上）
１６．设{an}为等差数列，从{a1，a2，a3，…，a10}中任取4个不同的数，使这4个数仍成等差数列，则这样的等差数列最多有 24 个．
三、解答题：本大题6小题，共70分．解答应写出文字说明，证明过程或演算步骤．
１７．(本小题满分12分)在△ABC中，a，b，c分别为角A，B，C的对边，且a，b，c成等比数列．(I)求∠B的范围；(II)求y＝2sin2B＋sin(2B＋)的取值范围．
解：(1)因为a，b，c成等比数列，所以b2＝ac．
根据余弦定理，得cosB＝＝≥＝．
又因为0＜B＜，所以0＜B≤．
所以∠B的范围是(0，]．
(2)y＝2sin2B＋sin(2B＋)＝1－cos2B＋sin2Bcos＋cos2Bsin
＝1＋sin2Bcos－cos2Bsin＝1＋sin(2B－)．
因为0＜B≤，所以－＜2B－≤，所以－＜sin(2B－)≤1，所以＜y≤2．
所以y＝2sin2B＋sin(2B＋)的取值范围是(，2]．
１８．(本小题满分14分)如图，在多面体ABCDE中，AE⊥面ABC，BD∥AE，且AC＝AB＝BC＝BD＝2，AE＝1，F为CD的中点．
(I)求证：EF⊥面BCD；
(II)求多面体ABCDE的体积；
(III)求面CDE与面ABDE所成的二面角的余弦值．
解：(I)取BC中点G，连FG，AG．
因为AE⊥面ABC，BD∥AE，所以BD⊥面ABC．
又AGÌ面ABC，所以BD⊥AG．
又AC＝AB，G是BC的中点，所以AG⊥BC，所以AG
平面BCD．
又因为F是CD的中点且BD＝2，所以FG∥BD且FG＝BD＝1，所以FG∥AE．
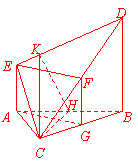又AE＝1，所以AE＝FG，所以四边形AEFG是平行四边形，所以EF∥AG，所以EF⊥BCD．
(II)设AB中点为H，则由AC＝AB＝BC＝2，可得CH⊥AB且CH＝．
又BD∥AE，所以BD与AE共面．
又AE⊥面ABC，所以平面ABDE⊥平面ABC．
所以CH⊥平面ABDE，即CH为四棱锥C－ABDE的高．
故四棱锥C－ABDE的体积为VC－ABDE＝SABDE·CH＝[(1＋2)×2×]＝．
(III)过C作CK⊥DE于K，连接KH．
由三垂线定理的逆定理得KH⊥DE，所以∠HKC为二面角C－DE－B的平面角．
易知EC＝，DE＝，CD＝2．
由S△DCE＝×2×＝×CK，可得CK＝．
在Rt△CHK中，sin∠HKC＝＝，所以cos∠HKC＝，
所以面CDE与面ABDE所成的二面角的余弦值为．
19．某汽车厂有一条价值为a万元的汽车生产线，现要通过技术改造来提高该生产线的生产能力，提高产品的增加值，经过市场调查，产品的增加值y万元与技术改造投入x万元之间满足：①y与(a－x)和x2的乘积成正比；②当
时，y=a3；③
，其中t是常数，且t
（1）设y=f(x)，求f(x)的表达式及定义域；
（2）求出产品增加值y的最大值及相应的x的值。
解：（1）设y=f(x)=k(a－x)x2
∵当时，y=a3，即
∴k=8
∴f(x)=8(a－x)·x2
∵
∴函数的定义域是
（2）f(x)=－24x2+16ax，令f’(x)=0，则x=0（舍），x=
当0<x<时，f’(x)>0，∴f(x)在
上是增函数
当x>时，f’(x)<0，∴f(x)在
上是减函数
所以x=为极大值点
当
时，即1≤t≤2，
当
时，即0<t<1，
综上：当1≤t≤2时，投入万元，最大增加值
当0<t<1时，投入
万元，最大增加值
２０．(本小题满分14分)设椭圆＋＝1(a＞b＞0)的离心率为e，A为椭圆上一点，弦AB，AC分别过焦点F1，F2．
(I)若∠AF1F2＝α，∠AF2F1＝β，试用α，β表示椭圆的离心率e；
(II)设→＝λ1→，→＝λ2→，当A在椭圆上运动时，求证：λ1＋λ2为定值．
.解：(I)设F1(－c，0)，F2(c，0)．在△AF1F2中，由正弦定理得
＝＝，
即 AF1＝，AF2＝，
所以 2a＝AF1＋AF2＝＋
＝2c(＋)＝2c·，
得 e＝．
(II)设A(x0，y0)，B(x1，y1)，C(x2，y2)．
①当y0＝0时，λ1＋λ2＝2＝；当AB或AC与x轴垂直时，λ1＋λ2＝．
②当AB，AC都不与x轴垂直且y0≠0时，AC的方程为y＝(x－c)，
由消x得[b2(x0－c)2＋a2y]y2＋2b2y0(x0－c)y＋c2b2y－a2b2y＝0．
由韦达定理得 y2y0＝，
所以 y2＝，
所以 λ2＝＝－＝－ ，
同理可得 λ1＝＝－＝－，
故 λ1＋λ2＝－[＋]
＝－＝＝＝，
综上可知 λ1＋λ2＝．
2１．
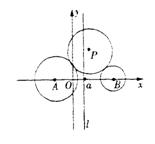已知两圆A：
，B：
，如图所示，动圆P与圆A和圆B都相外切，直线l的方程为x=a
（a
）
（1）求动圆P的圆心的轨迹方程，并证明：当a=
时，点P到点B的距离与到定直线l的距离之比为定值。
（2）延长PB与点P的轨迹交于另一点Q，求PQ的最值。
（3）延长PB与点P的轨迹交于另一点Q，如果存在某一位置，使得PQ的中点R在l上的射影C满足PC⊥QC，求a的取值范围。
．解：（1）设动圆P的半径为r，则PA=r+
，PB=r+，∴PA－PB=2，∴点P的轨迹是以A、B为焦点，焦距为4，实轴长为2的双曲线的右支，其方程为
若a=，则l为双曲线的右准线，∴点P到点B的距离与到l的距离之比为双曲线的离心率e=2
（2）若PQ的斜率存在，设斜率为k，则直线PQ的方程为y=k(x－2)，代入双曲线方程得(3－k2)x2+4k2x－4k2－3=0
由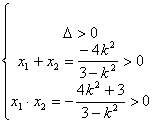
，解得k2>3
∴PQ=
当直线斜率不存在时，x1=x2=2得，y1=3，y2=－3，PQ=6
∴PQ的最小值为6
（3）当PC⊥QC时，P、C、Q构成直角三角形
∴R到直线l的距离RC=
=xR－a
1
又点P、Q都在双曲线
上
∴
，
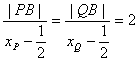即PQ=4xR－2，xR=
2
将②代入①得
PQ=2－4a≥6 ∴a≤－1