文科数学高考复习作业（1）
班级 姓名 座号
1、给出两个命题：
：
的充要条件是
为正实数；
：不等式
取等号的条件是
异号，则下列哪个复合命题是真命题 （ ）
A．
B．
C．
D．
2、函数
的图象大致是 （ ）
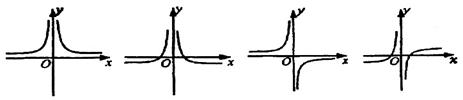
A． B． C． ．
3、△ABC中，C=2B，则
等于
（ ）
A．
B．
C．
D．
4、数
的图象按向量
平移，得到
的图象，则
（ ）
A．
B．
C. 
D. 
5、6支签字笔与3本笔记本的金额之和大于24元，而4支签字笔与5本笔记本的金额之和小于22元，则2支签字笔与3本笔记本的金额比较结果是（ ）
A．3本笔记本贵 B．2支签字笔贵 C．相同 D．不确定
6、如图，在
中，
，AC、BC边
上的高分别为BD、AE，则以A、B为焦点，且过D、E的椭圆
与双曲线的离心率的倒数和为（ ）
A．
B．
C．
D．
7、用火柴棒按下图的方法搭三角形，则按图示的规律搭下去，则所用火柴棒数an与所搭三角形的个数n之间的关系式可以是
.
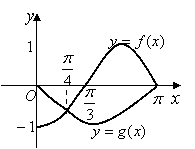8、已知函数
是偶函数，
是奇函数，
它们的定义域是
，且它们在
上的图象
如图所示，则不等式
的解集是
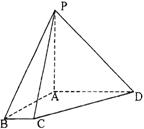
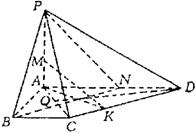
9、已知四边形ABCD中，
，
平面ABCD，
|
的比为2，求二面角M—CD—A的正切值.
10、一种电路控制器在出厂时每四件一等品装成一箱，工人在装箱时不小心把两件二等品和两件一等品装入了一箱，为了找出该箱中的二等品，对该箱中的产品逐一取出进行测试.
（1）求前两次取出的都是二等品的概率；
（2）求第三次取出全部二等品的概率.
作业（1）答案：1、D2、D3、A4、C5、B6、A7、
8、 
9.解法一：（1）过D作DQ⊥AC于点Q，
平面ABCD，
.………………（1分） 
平面PAC.………………（2分）
∴又由
|
……………（4分）
………（5分）
∴D到平面PAC的距离为
…………（6分）
（2）过A作AK⊥DC于K点，连MK. ∵PA⊥平面ABCD，∴MK⊥CD.∴∠MKA为M—CD—A的平面角.…（9分）
中，
由面积相等，得
（12分）
解法二：以A为坐标原点，分别以
所在直线为x、y、z轴建立坐标系.
……………………………………（1分）
（1）过D作
就是D到平面PAC
的距离.………………（2分）
设
…………（4分）
由
…………（5分）
……………………（6分）
（2）过A作
………………（7分）
则
………………（9分）
就是M—CD—A的平面角.……（11分）
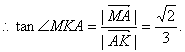………………………………（12分）
10. 解：（1）四件产品逐一取出排成一列共有A
种方法，前两次取出的产品都是二等品的共有
种方法，∴前两次取出的产品都是二等品的概率为
；…………………………6分
（2）四件产品逐一取出排成一列共有A种方法，第二次取出的产品是四等品的共有
种方法，∴前三次取出全部产品是二等品的概率为1－
；……………………13分