最新高考数学模拟试卷(文科)(06 年 08月29 )
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分.考试用时120分钟.
第Ⅰ卷 选择题(共50分)
一、选择题:本大题共10小题,每小题5分,共50分. 在每小题给出的四个选项中,只有一项是符合题目要求的.
1、
已知集合![]() ,
,![]() ,则
,则![]()
A .![]() ; B .
; B .![]() ; C .
; C .![]() ;
D .
;
D .![]()
2、 函数![]() 的定义域是
的定义域是
A .![]() ; B .
; B .![]() ; C
.
; C
.![]() ; D .(-1,0)
; D .(-1,0)
3、
若把函数![]() 的反函数记为
的反函数记为![]() ,则
,则![]()
A .![]() ;
B .2; C .
;
B .2; C .![]() ;
D .
;
D . ![]()
4、已知函数![]() ,则
,则![]()
A .0;
B .1;
C .3;
D .![]()
5、
二次函数![]() 在
在![]() 上是减函数,则实数
上是减函数,则实数![]() 的取值范围是
的取值范围是
A .![]() ; B .
; B .![]() ; C .
; C .![]() ; D .
; D .![]()
6、设![]() ,
,![]() ,
,![]() ,则
,则
A .![]() ; B .
; B .![]() ; C
.
; C
.![]() ; D .
; D .![]()
7、计算![]()
A.2.9; B.3.1 C.4.9 D.5.1
8、方程![]() 的一个实根存在的区间是(参考:
的一个实根存在的区间是(参考:![]() )
)
A .![]() ; B .
; B .![]() ; C.
; C.![]() D .
D .![]() ;
;
9、已知映射![]() ,其中
,其中![]() ,
,![]() ,对应法则为
,对应法则为![]() ;对于
;对于![]() ,但在集A中找不到原像,则实数
,但在集A中找不到原像,则实数![]() 的取值范围为
的取值范围为
A .![]() ;
B .
;
B .![]() ;
C .
;
C .![]() ; D .
; D .![]()
10、已知![]() ,
,![]()
![]() 且
且![]() ,且
,且![]() ;则
;则![]() 在同一坐标系内的图象大致是
在同一坐标系内的图象大致是
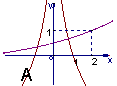
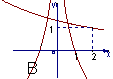
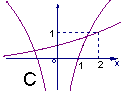
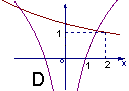
第Ⅱ卷非选择题(共100分)
二、填空题:本大题共4小题,每小题5分,共20分.
11、已知![]() ,
,![]() ,若
,若![]() ,则
,则![]()
12、若复数![]() 满足
满足![]() ,则
,则![]() ;若复数
;若复数![]() 满足
满足![]() ,则
,则![]()
13、已知等比数列![]() 中,
中,![]() ,
,![]() ,则公比
,则公比![]()
14、规定记号“![]() ”表示一种运算,即
”表示一种运算,即![]()
![]() ,且
,且![]() 。若函数
。若函数![]() 的最小值为
的最小值为![]() ,则
,则![]()
三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.
15、(12分)已知函数![]() ,
,
①若![]() ,求函数
,求函数![]() 的最大值与最小值。
的最大值与最小值。
②若![]() ,且
,且![]() ,求
,求![]() 的值。
的值。
16、(13分)某人依次抛出两枚均匀骰子(它们的六个面分别标有点数1、2、3、4、5、6),
①(6分)求两次点数相同的概率。 ②(7分)求两次点数之和为4的概率。
17、(13分)已知函数![]() ,设
,设![]() ,
,![]()
![]()
(1)(6分)求![]() ,
,![]() 的表达式,并猜想
的表达式,并猜想![]()
![]() 的表达式(直接写出猜想结果)
的表达式(直接写出猜想结果)
 (2)(7分)求关于
(2)(7分)求关于![]() 的二次函数
的二次函数![]()
![]()
![]() 的最小值。
的最小值。
18、(14分)已知函数![]() 为自然对数的底数
为自然对数的底数![]() ,
,
①(3分)判断函数![]() 的奇偶性。
的奇偶性。
②(3分)若![]() ,求常数
,求常数![]() 的值与函数
的值与函数![]() 的表达式。
的表达式。
③(4分)求证:![]() 。
。
④(4分)求函数![]() 的反函数。
的反函数。
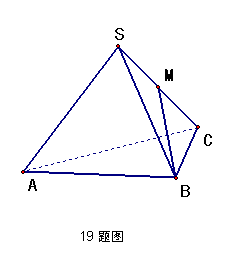
19、(14分)已知边长为2的正四面体![]() (六条棱的长均相等)中,
(六条棱的长均相等)中,
点![]() 为棱
为棱![]() 的中点,
的中点,
①求证:![]()
②若异面直线![]() 与
与![]() 所成的角为
所成的角为![]() ,求
,求![]() 的值。
的值。
20、(14分)已知椭圆![]() 的焦点分别为
的焦点分别为![]() 、
、![]() ,长轴长为6,设直线
,长轴长为6,设直线![]() 交椭圆
交椭圆![]() 于A、B两点。
于A、B两点。
①(8分)求线段AB的中点坐标;②(6分)求![]() 的面积。
的面积。
附中高三 文 科 暑假补课 数学答案(时间: 06、08、25 )
一、选择题答题卡(10![]() 5=50)
5=50)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | D | C | C | B | A | D | C | C | A | B |
二、填空题答题卡(4![]() 5=20)
5=20)
11 3
; 12 ![]() ;
; ![]()
13 ![]() ; 14
0
;
; 14
0
;
三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.
15题( 12 分):
解:① ![]() ,
,![]() ,
,![]() ,
,![]() (6分)
(6分)
②
解一、![]() ,
,![]() ,
,![]() ,又
,又![]() ,
,
![]() ,
, ![]() 。 (12分)
。 (12分)
解二、![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() 。 (12分)
。 (12分)
16题( 13 分):
解:①设“两次点数相同”为事件![]() ,则
,则![]() 。(6分)
。(6分)
②设“两次点数之和为4”为事件![]() ,则
,则![]() 。(13分)
。(13分)
17题( 13 分):
解:① ![]()
![]() ,
,![]() ,
,![]()
![]()
![]() ,
,
同理![]() 。从而猜想
。从而猜想![]() 。(6分)
。(6分)
② ![]()
![]()
![]()
![]()
由①知,![]()
![]()
![]() ,
,![]() ,
,
![]() 关于
关于![]() 的二次函数
的二次函数![]()
![]()
![]() 的最小值为
的最小值为![]() 。(13分)
。(13分)
18题( 14分):
解:① ![]() 的定义域为
的定义域为![]() 关于原点对称,
关于原点对称,![]()
![]() 为奇函数。(3分)
为奇函数。(3分)
② ![]()
![]()
又![]() ,
,![]() ,
,![]() 。(6分)
。(6分)
③ 解一、由②知![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,即
,即![]() ,
,![]() 。(10分)
。(10分)
解二、设![]() ,则
,则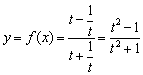 ,
,![]() ,
,
![]()
![]() 。(10分)
。(10分)
解三、由②知![]() ,
,![]() ,(10分)
,(10分)
④ 由②知![]() ,
,![]() ,
,![]() ,
,![]() 的反函数为
的反函数为
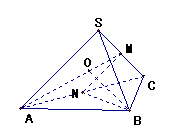
![]() 。(14分)
。(14分)
19题( 14分):
①:
证法一、如图连接![]() ,在正四面体
,在正四面体![]()
(六条棱的长均相等)中,有![]() 与
与![]() 均是正三角形,
均是正三角形,
![]() ,
,![]() ,
,![]() 面
面![]() ,
,![]() 面
面![]() ,
,
![]() 。(7分)
。(7分)
证法二、在正四面体![]() (六条棱的长均相等)中,有
(六条棱的长均相等)中,有![]() 是正三角形,设点
是正三角形,设点![]() 为正
为正![]() 的中心,连接
的中心,连接![]() 、
、![]() ,则
,则![]() 面
面![]() ,
,![]() ,由三垂线定理得
,由三垂线定理得![]() 。(7分)
。(7分)
②
解:在边长为2的正四面体![]() (六条棱的长均相等)中,取棱
(六条棱的长均相等)中,取棱![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,在
,在![]() 中,
中,![]() ,
,![]() 是
是![]() 的中位线,
的中位线,![]() ,
,![]() ,则
,则![]() ,
,![]() ,从而
,从而![]() 是锐角三角形,
是锐角三角形,![]() ,由余弦定理得
,由余弦定理得
![]() 。(14分)
。(14分)
20题( 14分):
解:①设椭圆C的方程为![]() (1分),由题意
(1分),由题意![]() ,于是
,于是![]() ,所以椭圆C的方程为
,所以椭圆C的方程为![]() (4分)。由
(4分)。由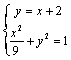 ,得
,得![]() (6分),由于该二次方程的
(6分),由于该二次方程的![]() ,所以点A、B不同。设
,所以点A、B不同。设![]() ,则
,则![]() ,故线段AB的中点坐标为
,故线段AB的中点坐标为![]() (8分)。
(8分)。
②
解一、设点O到直线![]() 的距离为
的距离为![]() ,则
,则![]() (10分),又
(10分),又![]() ,所以
,所以![]() (13分),
(13分),
所以![]() (14分)
(14分)
解二、设直线![]() 与
与![]() 轴交于点
轴交于点![]()
![]() ,则
,则![]() ,
,
由①可知,![]() ,
,![]()
,则![]()
![]() 。(14分)
。(14分)