保定市2006年高考模拟考试
数学试题(文史财经类)
命题人:蒋文利 陈云平 冯振好2006.4.7
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。共150分,考试用时120分钟。
(第Ⅰ卷选择题部分,共60分)
一、选择题:(本大题共12小题,每个小题5分,共60分,在每小题给出的四个选项中,只有一个是符合要求的)
1、已知全集![]() ,集合
,集合![]()
![]() 则
则![]() 为 A.
为 A.![]() B.{1,2} C.
B.{1,2} C. ![]() D.
D. ![]()
2、在等差数列![]() 中,
中,![]() ,
,![]() 成等比数列, 则等差数列的公差是( ) A、–5或1 B、1 C、 –3 D、–3或3
成等比数列, 则等差数列的公差是( ) A、–5或1 B、1 C、 –3 D、–3或3
3、甲、乙各掷一次飞镖,假设二人击中目标的概率均为0.6,则至少有一人击中目标的概率为
A 0.36 B 0.16 C 0.48 D 0.84
4、给出下列条件(其中![]() 和
和![]() 为直线,
为直线,![]() 为平面)
为平面)
①![]() 内的一凸五边形的两条边,②
内的一凸五边形的两条边,②![]() 内三条不都平行的直线,
内三条不都平行的直线,
③![]() 内无数条直线,④
内无数条直线,④![]() 内正六边形的三条边。
内正六边形的三条边。
其中是![]() 的充分条件的所有序号是( )
的充分条件的所有序号是( )
A ② B ①③ C ②④ D ③④
5、不等式![]() 的解集是( )
的解集是( )
A.![]() B.
B. ![]()
![]()
![]()
C. ![]()
![]() D.
D. ![]()
![]()
![]()
![]()
![]()
6、样本(0,2,4,6,8)是随机地从总体M中抽取的,则总体的方差是( )
A.8 B.6 C.4. D.10
7、已知正三棱柱ABC-A1B1C1中,E是BC的中点,D是AA1上的一个动点,且![]() ,若
,若![]() ∥平面DB1C,则
∥平面DB1C,则![]() 的值等于
的值等于 ![]()
8、![]() 展开式的第三项为10,则y关于x的函数图象的大致形状为
展开式的第三项为10,则y关于x的函数图象的大致形状为
 |
9、用0、1、2、3、4的五个数组成无重复数字的五位数,奇数数字相邻,偶位数也全相邻的有
A、32个 (B)24个 (C)20个 (D)36个
10、两个正数m,n的等差中项是5,等比中项是4,且m>n,则椭圆![]() 的离心率e等于
的离心率e等于
A.![]() B.
B.
![]() C.
C. ![]() D.
D.
![]()
11、已知二次函数![]() 在点
在点![]() 处的切线为
处的切线为![]() ,设函数
,设函数![]() 若
若![]() 恒成立,则
恒成立,则
A.![]() B.
B.![]() C.
C.![]() ; D.
; D.![]()
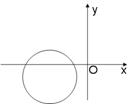 12、若右图,定圆的半径为a,圆心为(b,c)则直线
12、若右图,定圆的半径为a,圆心为(b,c)则直线
![]() 与直线
与直线![]() 的交点在
的交点在
A.第一象限 B.第二象限 C.第三象限D. 第四象限
第Ⅱ卷(非选择题部分,共90分)
二、填空题:(本题共4个小题,每小题4分,共16分。把正确的答案填在题后的横线上。)
13、向量a,b满足a=1,b=2,且3a+2b=(1,2),则a与b的夹角的余弦值为
14、与抛物线x2=4y关于直线x+y=0对称的抛物线的焦点坐标是 .
15、十届全国人大四次会议,提出了建设资源节约型、环境友好型社会的战略目标.为此,某企业决定,要在未来几年里,力争通过技术创新,使企业平均每年比上一年总产值增长10%、总成本降低20%.若去年的总产值和总成本分别为3百万元和1百万元,则从今年起,大约经过 年,可使企业纯利润比去年翻一番.
16给出下列命题:
①若α,β是三角形内角,且α>β,则cosα<cosβ;
②函数![]() 的单调增区间是
的单调增区间是![]()
③![]() 是以
是以![]() 为周期且在
为周期且在![]() 上单调递增的偶函数
上单调递增的偶函数
④把函数![]() 的图象按向量
的图象按向量![]() 平移,得到函数
平移,得到函数![]() 的图象.其中正确命题的序号有
(把你认为正确的都填上)
的图象.其中正确命题的序号有
(把你认为正确的都填上)
三、解答题:(本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤。)
17、(本小题满分12分)
已知![]() ,
,
⑴求tan![]() 的值
的值
⑵求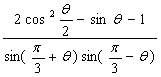 的值
的值
18、(本小题满分12分)
已知Sn为数列{an}的前n项和, ![]() = (
= (![]() , 2)与
, 2)与 ![]() = (
= (![]() -1, 1)共线
-1, 1)共线
(1) 求数列{n![]() }的前 n项和
}的前 n项和![]()
(2)若对任意n![]() N* ,K
N* ,K![]() +
+![]() ≤4
≤4![]() +14成立,试求实数K的最大值。
+14成立,试求实数K的最大值。
 19、(本小题满分12分)
19、(本小题满分12分)
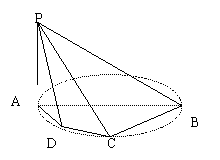
已知:如图,PA![]() ⊙o,PA=2,AB为直径,
⊙o,PA=2,AB为直径,
其长为4,四边形ABCD内接于圆O,且![]()
⑴求证:PB2=PC2+BC2
⑵求点C到平面PAB的距离;
⑶若D为![]() 的中点,求二面角D-PC-B的大小.
的中点,求二面角D-PC-B的大小.
20、(本小题满分12分)
要将甲、乙两种大小不同的钢板截成A、B两种规格,每张钢板可同时截得A、B两种规格的小钢板的块数如下表所示:
|
钢板类型 | A | B |
| 甲 | 2 | 1 |
| 乙 | 1 | 3 |
已知库房中现有甲、乙两种钢板的数量分别为5张和10张,市场急需A、B两种规格的成品数分别为15块和27块.
⑴问各截这两种钢板多少张可得到所需的成品数,且使所用的钢板张数最少?
⑵若某人对线性规划知识了解不多,而在可行域的整点中随意取出一解,求其恰好取到最优解的概率.
21、(本小题满分12分)
已知函数![]() ,
, ![]() 为其图像上任意一点,过点
为其图像上任意一点,过点![]() 的切线的斜率
的切线的斜率![]() ,且函数
,且函数![]() 有极小值1,
有极小值1,
(1)求函数![]() 的表达式及其函数
的表达式及其函数![]() 的极大值.
的极大值.
(2)当-2≤x≤4时,讨论方程f(x)=m的解的个数
22、(本小题满分14分)
已知曲线![]() 及直线
及直线![]() ,
,
(1)若![]() 与曲线
与曲线![]() 的右支有两个不同的交点,求实数
的右支有两个不同的交点,求实数![]() 的取值范围;
的取值范围;
(2)若![]() 与
与![]() 交于A、B两点,O为坐标原点,且满足
交于A、B两点,O为坐标原点,且满足![]() ,求实数
,求实数![]() 的值。
的值。
参考答案:
一、选择CDDCD ACBDC BA
二、填空 13
![]() 14
.(-1,0) 15. 4 16. ① ②③
14
.(-1,0) 15. 4 16. ① ②③
三、解答题
17、解![]() 由已知得
由已知得![]() ①,平方得1-2
①,平方得1-2![]() 即
即![]() ②,联立①②得
②,联立①②得![]()
![]()
![]()
⑵原式=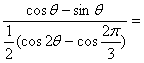
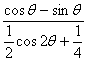 =
=![]()
18、解:本题注重考察数列、向量、不等式知识间的综合运用。
(1)∵ ![]() =(Sn,
2) 与
=(Sn,
2) 与 ![]() =(an-1,1)共线 ∴Sn-2(an-1)=0
=(an-1,1)共线 ∴Sn-2(an-1)=0
∴Sn=2an-2 又a1=s1 ∴a1=2 当n≥2时 Sn-1=2an-1-2
∴Sn-Sn-1=2an-2an-1 ∴an=2an-2an-1
![]()
![]() ∴
∴ ![]() = 2 即{an}是以2为首项2为公比的等比数列∴an=2n
= 2 即{an}是以2为首项2为公比的等比数列∴an=2n
∴Tn=1·2+2·22+3·23+…+n·2n
2Tn=1·22+2·23+…(n-1)·2n+n·2n+1
∴-Tn=2+22+……+2n -n·2n+1
∴Tn+(n-1)2n+1+2
(2)∵an=2n Sn=2n+1-2 Kan+Sn≤4n+14
K2n+2n+1-2≤4n+14 ∴(K+2)2n≤4n+16
∴K≤2n+![]() -2又2n+
-2又2n+![]() -2≥6
-2≥6
(当且仅当n=2时取等号)∴K≤6,即K的最大值为6
19、⑴连结AC, 因为AB为直径,所以![]()
又PA![]() ⊙o,AC是PC在圆面上的射影,
⊙o,AC是PC在圆面上的射影,
所以![]() ,
,
即 PB2=PC2+BC2
⑵过C点作CE![]() AB,垂足为E,因为PA
AB,垂足为E,因为PA![]() ⊙o面,所以,面ABC⊥面PAB
⊙o面,所以,面ABC⊥面PAB
,于是![]() ,即CE就是点C到平面PAB的距离,
,即CE就是点C到平面PAB的距离,
因为AB为直径,![]() ,所以
,所以![]()
又AB=4,所以,BC=2,AC=2![]() ,
,
所以CE=AC×BC/AB=![]()
⑶因为![]() 又D为
又D为![]() 的中点,连AC,
的中点,连AC,
作![]() 于M,过M做
于M,过M做![]() 由三垂线定理得∠MND为二面角D-PC-A的平面角,
由三垂线定理得∠MND为二面角D-PC-A的平面角,
在三角形MND中可求得∠MND=arctan![]() 由第⑴问知二面角B-PC-A是直二面角
由第⑴问知二面角B-PC-A是直二面角![]() 面角D-PC-B的大小为
面角D-PC-B的大小为![]()
20、解:设需截甲、乙两种钢板的张数分别为x、y,则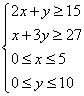
作出可行域如图 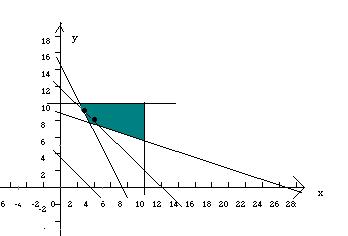
⑴因为,目标函数为z=x+y(x、y为整数),所以在一组平行直线x+y=t(t为参数)中,经过可行域内的整点且与原点距离最近的直线是x+y=12,其经过的整点是(3,9)和(4,8),它们都是最优解.
⑵因为可行域内的整点个数为8个,而最优解有两个,所以所求的概率为p=2/8=0.25
答:两种钢板的张数分别为3、9或4、8.概率为0.25
21、

(2)由(1)知f(x)在![]()
![]() 是增函数,(0,2)上是减函数,
是增函数,(0,2)上是减函数,
易得m=1或![]() 时两个根;m
时两个根;m![]() 三个根;
三个根;![]() 或
或![]() 一个解,其他无解
一个解,其他无解
22(1)解:由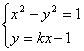 ,消去
,消去![]() 得
得![]() ,
,
由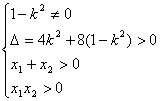 ,
,
∴![]() 的取值范围为
的取值范围为![]() 。
。
(2)设![]()
由(1)得![]()
而![]()
即![]()
也即![]()
又![]() 过点
过点![]() ,∴
,∴![]()
即![]()
∴![]() .
.