第二章 数列
考试内容：
数列。
等差数列及其通项公式。等差数列前n项和公式。
等比数列及其通项公式。等比数列前n项和公式。
教学目标
（1）理解数列的概念，了解数列通项公式的意义；了解递推公式是给出数列的一种方法，并能根据递推公式写出数列的前几项。
（2）理解等差数列的概念，掌握等差数列的通项公式与前n项和公式，并能解决简单的实际问题。
（3）理解等比数列的概念，掌握等比数列的通项公式与前n项和公式，并能解决简单的实际问题。
1985——2002年高考试题集锦
一、选择题
1. 给出20个数:87，91，94，88，93，91，89，87，92，86，90，92，88，90，91，86，89，92，95，88.它们的和是( )(86年(5)3分)
(A)1789 (B)1799 (C)1879 (D)1899
2. 设命题甲:△ABC的一个内角为60o，命题乙:△ABC的三个内角的度数成等差数列.那么( )(88年(11)3分)
(A)甲是乙的充分不必要条件 (B)甲是乙的必要不充分条件
(C)甲是乙的充要条件 (D)甲不是乙的充分条件也不是乙的必要条件
3. 已知{an}是等比数列,如果a1＋a2＋a3＝18,a2＋a3＋a4＝－9,Sn＝a1＋a2＋……＋an,那么
的值等于( )(89年(5)3分)
(A)8 (B)16 (C)32 (D)48
4. 已知{an}是等比数列,且an＞0,a2a4＋2a3a5＋a4a6＝25,那么a3＋a5＝( )(91年(7)3分)
(A)5 (B)10 (C)15 (D)20
5. 在各项均为正数的等比数列{an}中,若a5a6＝9,则log3a1＋log3a2＋……＋log3a10＝( )(93年(7)3分)
(A)12 (B)10 (C)8 (D)2＋log35
6. 某种细菌在培养过程中,每20分钟分裂一次(一个分裂为两个),经过3个小时,这种细菌由一个可繁殖成( )(94年(5)4分)
(A)511个 (B)512个 (C)1023个 (D)1024个
7. 等差数列{an}，{bn}的前n项和分别为Sn,Tn,若
＝( )(95年(12)5分)
(A)1 (B)
(C)
(D)
8. 等比数列an的首项a1＝－1，前n项和为Sn，已知
等于( )(96年(10)4分)
(A) (B)－ (C)2 (D)－2
9. 等差数列{an}的前m项和是30，前2m项和是100，则它的前3m项和是( )(96年(12)5分)
(A)130 (B)170 (C)210 (D)260
10. 在等比数列{an}中,a1＞1,且前n项和Sn满足
,那么a1的取值范围是( )(98年(15)5分)
(A)(1,＋∞) (B)(1,4) (C)(1,2) (D)(1,
)
二、填空题
1. 已知等比数列{an}的公比q＞1，a1＝b(b≠0)，则
＝_______.(88年(24)4分)
2. 已知等差数列{an}的公差d≠0，且a1，a3，a9成等比数列，则
的值是_________.(92年(23)3分)
三、解答题
1. 设a
(n＝1,2,3……),
Ⅰ.证明不等式
对所有的正整数n都成立;
Ⅱ.设b
(n＝1,2,3……),用极限定义证明
.(85年(16)10分)
2. 已知x1＞0,x1≠1,且x
(n＝1,2,3……).试证:数列{xn}或者对任意的自然数n都满足xn＜xn＋1,或者对任意的自然数n都满足xn＋1＜xn.(86年(22)12分)
3. 设数列a1,a2,……an,……的前项和Sn与an的关系是Sn＝－ban＋1－
,其中b是与n无关的常数,且b≠－1,
Ⅰ.求an和an＋1的关系式;
Ⅱ.写出用n和b表示an的表达式;
Ⅲ.当0＜b＜1时,求极限
Sn.(87年(20)12分)
4. 是否存在常数a,b,c,使得等式1·22＋2·32＋……＋n(n＋1)2＝
(an2＋bn＋c)对一切自然数n成立？并证明你的结论.(89年(23)10分)
5. 有四个数,其中前三个数成等差数列,后三个数成等比数列,并且第一个数与第四个数的和是16,第二个数与第三个数的和是12,求这四个数.(90年(21)10分)
6. 设等差数列{an}的前n项和为Sn,已知a3＝12,S12＞0,S13＜0,
Ⅰ.求公差d的取值范围;
Ⅱ.指出S1,S2,……S12中哪一个值最大,并说明理由.(92年(27)10分)
7. 设{an}是正数组成的数列,其前n项的和为Sn,并且对所有的自然数n,an与2的等差中项等于Sn与2的等比中项,
Ⅰ.写出数列{an}的前3项;
Ⅱ.求数列{an}的通项公式(写出推导过程);
Ⅲ.令b
,(n∈N),求(b1＋b2＋……＋bn－n).(94年(25)14分)
8. 设{an}是由正数组成的等比数列,Sn是其前n项和,
Ⅰ.证明:
(lgSn＋lgSn＋2)＜lgSn＋1;
Ⅱ.是否存在常数c＞0,使得[lg(Sn－c)＋lg(Sn＋2－c)]＜lg(Sn＋1－c)成立?并证明你的结论.(95年(25)12分)
9. 已知数列{an},{bn}都是由正数组成的等比数列,公比分别为p,q,其中p＞q,且p≠1,q≠1.设cn＝an＋bn,Sn为数列{cn}的前项和,求
.(97年(21)11分)
10. 已知数列{bn}是等差数列,b1＝1,b1＋b2＋……＋b10＝145.
①求数列{bn}的通项bn;
②设数列{an}的通项an＝loga(1＋
)(其中a>0且a≠1),记Sn是数列{an}的前n项和.试比较Sn与
的大小,并证明你的结论.(98年(25)12分)
11. 
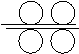右图为一台冷轧机的示意图,冷轧机由若干对轧辊
组成,带钢从一段输入,经过各队轧辊逐步减薄后输出
(1)输入带钢的厚度为α,输出带钢的厚度为β,若每对轧辊
的减薄率不超过r0,问冷轧机至少需要安装多少对轧辊?
(一对轧辊减薄率＝
)
(2)已知一台冷轧机共有4对减薄率为20%的轧辊,所有轧辊周长均为1600mm,若第k对轧辊有缺陷,每滚动一周在带钢上压出一个疵点,在冷轧机输出的带钢上,疵点的间距为Lk,为了便于检修,请计算L',L2,L3并填入下表(轧钢过程中,带钢宽度不变,且不考虑损耗)(99年(22)12分)
| 轧辊序号k | 1 | 2 | 3 | 4 |
| 疵点间距Lk(单位:mm) | 1600 |
12. 已知函数y＝f(x)的图象是自原点出发的一条折线,当n≤y≤n＋1(n＝0,1,2,…)时,该图象是斜率为bn的线段(其中正常数b≠1),设数列{xn}有f(xn)＝n(n＝1,2,…)定义
(1)求x1,x2和xn的表达式;(2)求f(x)的表达式,并写出其定义域
(3)证明y＝f(x)的图象与y＝x的图象没有横坐标大于1的交点(99年(23)14分)