浙江温州市省一级重点中学高三3月份联考
数学 (文科) 试卷
注意事项:
本试卷分为第Ⅰ卷(选择题)第Ⅱ卷(非选择题)两部分,共8页,满分为150分,考试时间为120分钟。
参考公式:如果事件A、B互斥,那么 球的表面积公式
P(A+B)=P(A)+P(B)
S=4![]() R2
R2
如果事件A、B相互独立,那么 其中R表示球的半径
P(A•B)=P(A)•P(B) 球的体积公式
如果事件A在一次试验中发生的概率是P,
![]()
那么n次独立重复试验中恰好发生k次的概率 其中R表示球的半径
![]()
一. 选择题 : (本大题共10小题, 每小题5分, 共50分. 在每小题给出的四个选项中, 有且只有一项是符合题目要求的,请将答案填写在答卷纸上)
1.设全集U={2,4,6,8}、集合A={2,a-2},![]() ,则实数a的值为( )
,则实数a的值为( )
A.-2或-6 B.-2或6 C.2或-6 D.2或6
2.“两条直线没有公共点”是“这两条直线异面”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3.已知函数![]() 的反函数为
的反函数为![]() ,则
,则![]() (1)等于( )
(1)等于( )
A.0 B.1 C.-1 D.4
4.等差数列{an}的前n项和为Sn,若a3+a7+a11=6,则S13=( )
A.24 B.25 C.26 D.27
5.若函数![]() 的图象按向量
的图象按向量![]() 方向平移可得到函数y=sin2
方向平移可得到函数y=sin2![]() 的图象,则
的图象,则![]() 可以是( )
可以是( )
A. (![]() ,0) B. (
,0) B. (![]()
![]() ,0) C. (
,0) C. (![]() ,0) D. (
,0) D. (![]()
![]() ,0)
,0)
6.对于一组数据![]() (
(![]() ,如果将它们改变为
,如果将它们改变为![]() ,则下面结论中正确的是( )
,则下面结论中正确的是( )
A.平均数与方差均不变 B. 平均数变了,而方差不变
C. 平均数与方差均变了 D. 平均数不变,而方差变了
7.在![]() 的展开式中,
的展开式中,![]() 3项的系数是
3项的系数是![]() 2项系数与
2项系数与![]() 5项系数的等比中项,则
5项系数的等比中项,则![]() 的值是( )
的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.在圆![]() 上的所有点中,到直线
上的所有点中,到直线![]() 的距离最大的点的坐标是( )
的距离最大的点的坐标是( )
A.(![]() ) B.(
) B.(![]() ) C.(
) C.(![]() ) D.(
) D.(![]() )
)
9.若![]() 的值域为
的值域为![]() ,则实数a的值是( )
,则实数a的值是( )
A.16 tx B.-16 C.32 D.-32
10.无论m为任何实数,直线![]() 与双曲线
与双曲线![]() (b>0)恒有公共点,则双曲线C的离心率e的取值范围是( )
(b>0)恒有公共点,则双曲线C的离心率e的取值范围是( )
A.(1,+∞) B.![]() C.
C.![]() D.(2,+∞)
D.(2,+∞)
二、填空题:(tx本大题共4小题,每小题4分,共16分.把答案填在答题卷上)
11.已知函数![]() 是一个以6为最小正周期的奇函数,则
是一个以6为最小正周期的奇函数,则![]() (3)= ▲
(3)= ▲
12.在半径为6的球面上有A、B两点,若线段AB=6,则A、B两点的球面距离为 ▲
13.有女学生5名,男学生2名,现从中选4人参加社区服务,必须有男学生参加的选法种数是 ▲ (用数字作答).
14.设抛物线![]() 的焦点为F,经过点P(2,1)的直线
的焦点为F,经过点P(2,1)的直线![]() 与抛物线相交于A、B两点且点P恰为AB的中点,则AF+BF= ▲
与抛物线相交于A、B两点且点P恰为AB的中点,则AF+BF= ▲
三、解答题(本大题共6个小题,共84分,解答应写出文字说明,证明过程或演算步骤)
15、(本小题满分14分)
设![]() ,
,![]()
(Ⅰ)求![]() 的最大值;
的最大值;
(Ⅱ)若![]() ,求
,求![]() 的值.
的值.
16.(本小题满分14分)
已知数列{an}的前n项和![]() ,其中a、b为常数
,其中a、b为常数
(Ⅰ)求出数列{an }的通项公式;
(Ⅱ)若数列{an }是等比数列,求a、b应满足的条件.
17.(本小题满分14分)
如图所示, ![]() VAD是等边三角形,ABCD是矩形, AB=
VAD是等边三角形,ABCD是矩形, AB=![]() BC,平面VAD
BC,平面VAD![]() 平面ABCD,F为AB中点.
平面ABCD,F为AB中点.
(Ⅰ)求VC与平面ABCD所成角的大小;
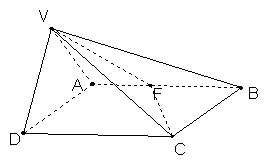 (Ⅱ)当V到平面ABCD的距离为3时,求B到平面VFC的距离.
(Ⅱ)当V到平面ABCD的距离为3时,求B到平面VFC的距离.
18.(本小题满分14分)
一台仪器每启动一次都随机地出现一个5位的二进制数![]() ,其中A的各位数字中,
,其中A的各位数字中,![]() 出现
出现![]() 的概率为
的概率为![]() ,出现1的概率为
,出现1的概率为![]() .例如:A=10001,其中
.例如:A=10001,其中![]() .记
.记![]() ,当启动仪器一次时,
,当启动仪器一次时,
(Ⅰ)设![]() 为事件B,求事件B的概率
为事件B,求事件B的概率![]() ;
;
(Ⅱ)设![]() 不大于3为事件C,求事件C的概率
不大于3为事件C,求事件C的概率![]() .
.
19.(本小题满分14分)
已知函数![]() ,
,![]()
![]()
(Ⅰ)若![]() 的图象与
的图象与![]() 的图象在x=2处的切线互相平行,求a的值;
的图象在x=2处的切线互相平行,求a的值;
(Ⅱ)若函数![]() 的两个极值点
的两个极值点![]() 恰是方程
恰是方程![]() 的两个根,求a、b的值;并求此时函数
的两个根,求a、b的值;并求此时函数![]() 的单调区间.
的单调区间.
20.(本小题满分14分)
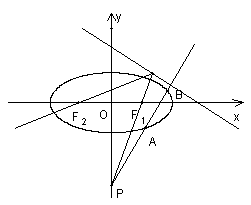
已知椭圆![]() 中心在原点,焦点在
中心在原点,焦点在![]() 轴上,离心率
轴上,离心率![]() ,光线从点
,光线从点![]() 出发经过右焦点
出发经过右焦点![]() ,到直线:
,到直线:![]() 后被它反射,反射光线经过左焦点
后被它反射,反射光线经过左焦点![]()
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)经过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
, ![]() 为
为![]() 轴上一点,若(
轴上一点,若(![]() )
)![]()
![]() ,求
,求![]() 的取值范围.
的取值范围.
数学 (文科) 参考答案
一、选择题 : (本大题共10小题, 每小题5分, 共50分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | B | C | C | A | B | D | A | D | B |
二、填空题:(本大题共4小题,每小题4分,共16分.把答案填在题中横线上)
11. 0 12.![]() 13. 30 14.
8
13. 30 14.
8
三、解答题(本大题共6个小题,共84分,解答应写出文字说明,证明过程或演算步骤)
15.解:(Ⅰ)![]() =
=![]()
![]() 的最大值为
的最大值为![]() ………………6分
………………6分
(Ⅱ)![]()
![]() ……9分
……9分
![]()
![]() =
=![]()
![]() ,
,![]()
![]()
![]() …………………………14分
…………………………14分
16.解:(Ⅰ)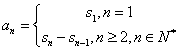 …………3分
…………3分
![]()
所以![]() ……………………7分
……………………7分
(Ⅱ)因为![]() 为等比数列
为等比数列![]() …………10分
…………10分
即![]() …………………………14分
…………………………14分
17.解法一:(Ⅰ)![]() ,
,
![]()
![]()
![]() ……………………3分
……………………3分
![]()
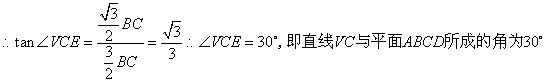 …………7分
…………7分
(Ⅱ)![]()
![]()
![]()
![]() ………………11分
………………11分
![]() 。……14分
。……14分
解法二:![]() ,取BC中点G,连EG,设BC=
,取BC中点G,连EG,设BC=![]() ,则AB=
,则AB=![]()
以E为原点,![]() 得:
得:
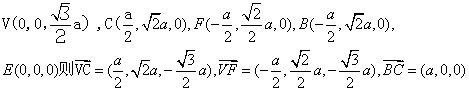 ……3分
……3分
设面VFC的一个法向量是![]()
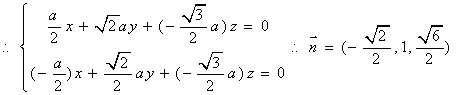 ……5分
……5分
B到平面VFC的距离为: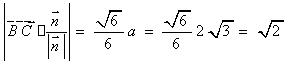 ……7分
……7分
18.解(Ⅰ)由题意得:![]() ……………………7分
……………………7分
(Ⅱ)![]() ………………14分
………………14分
19.解:![]() ………………1分
………………1分
(Ⅰ)![]() …………4分
…………4分
(Ⅱ)令![]()
分别代入![]() ……7分
……7分
![]() ………………10分
………………10分
此时![]()
![]()
![]() ................14分
................14分
20.解:(Ⅰ)设椭圆![]() 的方程为:
的方程为:![]() ,点
,点![]() 关于直线:
关于直线:![]() 的对称点
的对称点![]() 的坐标分别为
的坐标分别为![]() , 则点
, 则点![]() 三点共线,
三点共线,
![]() ,
,![]() ,………3分
,………3分
又椭圆的离心率![]() ,
,![]() ,椭圆
,椭圆![]() 的方程为:
的方程为:![]() .……5分
.……5分
(Ⅱ)因为(![]() )
)![]() ,所以
,所以![]() ,
,
D是线段AB的中垂线与![]() 轴的交点,……7分,
轴的交点,……7分,
设:![]() ,AB的中点
,AB的中点![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,
,
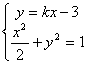 消去
消去![]() 得:
得:![]() ,…………9分
,…………9分
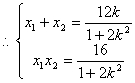
![]()
线段AB的中垂线方程为:![]() ,……12分
,……12分
![]()
又当![]() 轴时,
轴时,![]() ………………14分
………………14分