南京市中华中学2006高三综合练习1(90分钟)
一、选择题:
1. 已知i,j为互相垂直的单位向量,a = i – 2j,b = i + λj且a与b的夹角为锐角,则实数![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2. 设集合M={-1,1,0},N={1,2,3,4,5}, 映射f: M→N,使对任意的x∈M,都有x+f(x)是奇数,这样的映射f的个数为( )
A.10 B.11 C.12 D.13
3. 设函数f(x)是定义在R上的以3为周期的奇函数,若f(1)>1,f(2)=![]() ,则( )
,则( )
![]()
4. 已知数列![]() 的通项公式
的通项公式![]() ,设其前n项和为Sn,则使
,设其前n项和为Sn,则使![]() 成立的自然数n
( )A.有最小值63 B.有最大值63 C.有最小值31 D.有最大值31
成立的自然数n
( )A.有最小值63 B.有最大值63 C.有最小值31 D.有最大值31
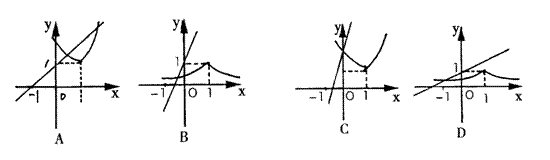 5. 已知函数
5. 已知函数![]() ,在同一直角坐标系中,
,在同一直角坐标系中,![]() 的图象可能是( )
的图象可能是( )
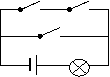
6. 设函数![]() ,若
,若![]() ,则下列不等式必定成立的是(
)
,则下列不等式必定成立的是(
)
A.![]() B.
B.![]() C.
C.
![]() D.
D. ![]()
7. 椭圆![]() 的长轴为A1A2,短轴为B1B2,将坐标平面沿y轴折成一个二面角,使A1点的平面B1A2B2上的
的长轴为A1A2,短轴为B1B2,将坐标平面沿y轴折成一个二面角,使A1点的平面B1A2B2上的
射影恰好是该椭圆的右焦点,则此二面角的大小为( )
A.30° B.45° C.60° D.75°
8. 已知α、β都是第二象限角,且cosα>cosβ,则( )
A.α<β B.sinα>sinβ C.tanα>tanβ D.cotα<cotβ
9.函数![]() 的图像按向量
的图像按向量![]() 平移后,所得函数的解析式是
平移后,所得函数的解析式是![]() ,则
,则![]() =(
)
=(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.设函数f(x+1)=x2-3x+2的定义域是(-∞,![]() ,则y=f-1(x)的表达式是( )
,则y=f-1(x)的表达式是( )
A![]() B
B![]() C.
C.![]() D.
D.![]()
11.已知函数![]() 在区间[-1,2
]上是减函数,那么b+c( )
在区间[-1,2
]上是减函数,那么b+c( )
A.有最大值![]() B. 有最大值
B. 有最大值![]() C.有最小值
C.有最小值![]() D. 有最小值
D. 有最小值![]()
二、填空题
12.如图,已知电路中![]() 个开关闭合的概率都是
个开关闭合的概率都是![]() ,且互相是独立的,则灯泡亮的概率是_____
,且互相是独立的,则灯泡亮的概率是_____
13.已知方程![]() 的四个根组成一个首项为
的四个根组成一个首项为![]() 的等比数列,则
的等比数列,则![]() _____
_____
14.已知有公共端点的向量a、b不共线,a=1,b=2.则与向量a、b的夹角平分线平行的单位向量是___
15.已知点P(2,-3),Q(3,2),直线ax+y+2=0与线段PQ相交,则实数a的范围是
16.符号![]() 表示不超过
表示不超过![]() 的最大整数,如
的最大整数,如![]() ,定义函数
,定义函数![]() ,那么下列命题中正确的是______
,那么下列命题中正确的是______
(1)函数![]() 的定义域为R,值域为
的定义域为R,值域为![]() ; (2)方程
; (2)方程![]() ,有无数解;
,有无数解;
(3)函数![]() 是周期函数; (4)函数
是周期函数; (4)函数![]() 是增函数; (5)函数
是增函数; (5)函数![]() 具有奇偶性。
具有奇偶性。
三、解答题
17.已知数列{![]() }满足前n项和为
}满足前n项和为![]() =n
=n![]() +1,数列{
+1,数列{![]() }满足
}满足![]() =
=![]() ,且前n项和为
,且前n项和为![]() .设
.设![]() =
=![]()
⑴求数列{![]() }的通项公式;⑵判断数列{
}的通项公式;⑵判断数列{![]() }的增减性;
}的增减性;
⑶当n≥2时![]() <
< ![]() -
-![]() 恒成立,求a的取值范围.
恒成立,求a的取值范围.
18.已知![]() 、
、![]() 分别是与x轴、y轴正方向相同的单位向量,
分别是与x轴、y轴正方向相同的单位向量,![]() (aÎR),对任意正整数n,
(aÎR),对任意正整数n,![]()
(1) 若![]() ,求a的值; (2) 求向量
,求a的值; (2) 求向量![]() ;
;
(3) 设向量![]() ,求最大整数a的值,使对任意正整数n,都有xn<yn成立。
,求最大整数a的值,使对任意正整数n,都有xn<yn成立。
19.若F1、F2分别为双曲线 -=1下、上焦点,O为坐标原点,P在双曲线的下支上,点M在上准线上,
且满足:![]() ,
,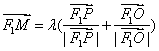 (
(![]() >0)。
>0)。
(1)求此双曲线的离心率; (2)若此双曲线过N(,2),求此双曲线的方程;
(3)若过N(,2)的双曲线的虚轴端点分别B1,B2(B2在x轴正半轴上),点A、B在双曲线上,
且![]() ,求
,求![]() 时,直线AB的方程。
时,直线AB的方程。
答案:
1. B
2. C
3. D
4. A
5. D
6. B
7. C
8. B
9. B
10. B
11. B
12.
![]()
13.
![]()
14.
![]()
15.
[-![]() ,
,![]() ]
]
16. ②③
![]() 17.解⑴
17.解⑴![]()
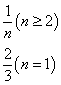
⑵![]() …
…![]() …
…![]() ,
,![]()
![]() 成递减数列。
成递减数列。
⑶由⑵![]() 为最大,
为最大,![]() 。
。
18.
(1) 由题意![]() ,∴51a120得
,∴51a120得![]()
(2) ![]()
![]()
![]()
(3)![]() ,由
,由![]() 恒成立,得
恒成立,得![]() 恒成立,令
恒成立,令![]() ,只需求数列{an}得最小项。由
,只需求数列{an}得最小项。由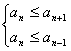 得6£n£6,即n=6,a6160
∴a=161
得6£n£6,即n=6,a6160
∴a=161
19.
(1) ![]()
![]() ,∴PF1OM为平行四边形,
,∴PF1OM为平行四边形,
又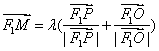 知M在∠PF1O的角平分线上,
知M在∠PF1O的角平分线上,
∴四边形PF1OM为菱形,且边长为![]() =c
=c
∴![]() =2a+
=2a+![]() =2a+c,由第二定义=e即=e,∴+1=e且e>1∴e=2
=2a+c,由第二定义=e即=e,∴+1=e且e>1∴e=2
(2)由e=2,∴c=2a即b2=3a2,双曲线方程为 -=1
又N(,2)在双曲线上,∴-=1,∴a2=3∴双曲线的方程为-=1
(3)由![]() 知AB过点B2,若AB⊥x轴,即AB的方程为x=3,此时AB1与BB1不垂直;
知AB过点B2,若AB⊥x轴,即AB的方程为x=3,此时AB1与BB1不垂直;
设AB的方程为y=k(x-3)代入-=1得(3k2-1)x2-18k2x+27k2-9=0
由题知3k2-1≠0且△>0即k2> 且k2≠,
设交点A(x1,y1),B(x2,y2),![]() =(x1+3,y1),
=(x1+3,y1),![]() =(x2+3,y2),
=(x2+3,y2),
∵![]() ,∴
,∴![]() =0即x1x2+3(x1+x2)+9+y1y2=0
=0即x1x2+3(x1+x2)+9+y1y2=0
此时x1+x2=,x1·x2=9,
y1y2=k2(x1-3) (x2-3)=k2[x1x2-3(x1+x2)+9]= k2[18-]=-
∴9+3+9-=0,∴5 k2=1,∴k=±
∴AB的方程为y=±(x-3),a<-1,∴a=-8