苏州市2006届高三教学调研测试
2006.1.21
一、选择题:
1、已知集合![]() ,集合
,集合![]() ,
,![]() ,则集合
,则集合![]()
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
2、已知等差数列![]() 的前
的前![]() 项和为
项和为![]() ,若
,若![]() ,则
,则![]() 等于
等于
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
3、不等式![]() 的解集是
的解集是
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
4、若函数![]() 的图象与
的图象与![]() 轴有两个交点,则实数
轴有两个交点,则实数![]() 的取值范围是
的取值范围是
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
5、抛物线![]() 的焦点坐标是
的焦点坐标是
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
6、设双曲线![]() 的右焦点为
的右焦点为![]() ,直线
,直线![]() 过点
过点![]() 且斜率为
且斜率为![]() ,若直线
,若直线![]() 与双曲线
与双曲线![]() 的左、右两支都相交,则直线
的左、右两支都相交,则直线![]() 的斜率的取值范围是
的斜率的取值范围是
A、![]() 或
或![]() B、
B、![]() 或
或![]() C、
C、![]() D、
D、![]()
7、若一系列函数的解析式和值域相同,但定义域互不相同,则称这些函数为“同族函数”,例如函数![]() ,
,![]() 与函数
与函数![]() ,
,![]() 即为“同族函数”。下面4个函数中,能够被用来构造“同族函数”的是
即为“同族函数”。下面4个函数中,能够被用来构造“同族函数”的是
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
8、已知函数![]() 是偶函数,则一定是函数
是偶函数,则一定是函数![]() 图象的对称轴的直线是
图象的对称轴的直线是
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
9、设![]() 、
、![]() 是不同的直线,
是不同的直线,![]() 、
、![]() 、
、![]() 是不同的平面,有以下四个命题:(1)
是不同的平面,有以下四个命题:(1)![]()
(2)![]() (3)
(3)![]() (4)
(4)![]() ,其中,假命题是
,其中,假命题是
A、(1)(2) B、(2)(3) C、(1)(3) D、(2)(4)
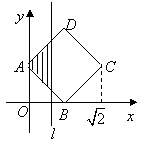 10、如图,正方形
10、如图,正方形![]() 的顶点
的顶点![]() ,
,![]() ,顶点
,顶点![]() 位于第一象限,直线
位于第一象限,直线![]() 将正方形
将正方形![]() 分成两部分,记位于直线
分成两部分,记位于直线![]() 左侧阴影部分的面积为
左侧阴影部分的面积为![]() ,则函数
,则函数![]() 的图象大致是
的图象大致是
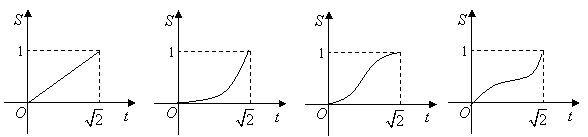 |
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
11、、已知直线![]() 是函数
是函数![]() 图象的一条对称轴,则函数
图象的一条对称轴,则函数![]() 图象的一条对称轴方程是
图象的一条对称轴方程是
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
12、已知等差数列![]() 的前
的前![]() 项的和为
项的和为![]() ,且
,且![]() ,
,![]() ,则过点
,则过点![]() 和
和![]() 的直线的一个方向向量的坐标是
的直线的一个方向向量的坐标是
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
二、填空题:
13、直角坐标系![]() 中,若定点
中,若定点![]() 与动点
与动点![]() 满足
满足![]() ,则点
,则点![]() 的轨迹方程是_
的轨迹方程是_
14、记地球的赤道的周长为![]() ,则地球北纬
,则地球北纬![]() 的纬线圈的周长用
的纬线圈的周长用![]() 表示等于______
表示等于______![]()
15、在右侧棋子堆放的示意图中,最上层(记为第一层)有一颗棋子,第二层有3颗,第三层有6颗,……,如果按图示的方式摆放,那么堆放满5层需要的棋子总数是_____颗
16、已知椭圆![]() 与双曲线
与双曲线![]() 在第一象限内的交点为
在第一象限内的交点为![]() ,则点
,则点![]() 到椭圆右焦点的距离等于______
到椭圆右焦点的距离等于______
17、设![]() ,
,![]() 是两个不共线的向量,若
是两个不共线的向量,若![]() ,
,![]() ,
,![]() ,且
,且![]() 三点共线,则
三点共线,则![]() _______
_______
18、若函数![]() 的图象与直线
的图象与直线![]() 有且仅有四个不同的交点,则
有且仅有四个不同的交点,则![]() 的取值范围是__________
的取值范围是__________
三、解答题:
19、已知函数![]()
(1)求![]() 的单调增区间
的单调增区间
(2)在直角坐标系中画出函数![]() 在区间
在区间![]() 上的图象。
上的图象。
20、已知函数![]() ,设
,设![]() ,
,![]()
![]()
(1)求![]() ,
,![]() 的表达式,并猜想
的表达式,并猜想![]()
![]() 的表达式(直接写出猜想结果)
的表达式(直接写出猜想结果)
(2)若关于![]() 的函数
的函数![]() 在区间
在区间![]() 上的最小值为6,求
上的最小值为6,求![]() 的值。
的值。
(符号“![]() ”表示求和,例如:
”表示求和,例如:![]() 。)
。)
21、如图,梯形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起,使点
折起,使点![]() 折到点
折到点![]() 的位置,且二面角
的位置,且二面角![]() 的大小为
的大小为![]()
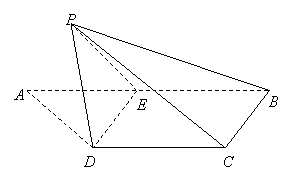 (1)求证:
(1)求证:![]()
(2)求直线![]() 与平面
与平面![]() 所成角的大小
所成角的大小
(3)求点![]() 到平面
到平面![]() 的距离
的距离
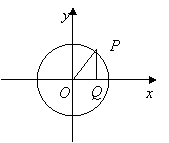 22、已知点
22、已知点![]() 是圆
是圆![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴于点
轴于点![]() ,设
,设![]()
(1)求点![]() 的轨迹方程
的轨迹方程
(2)求向量![]() 和
和![]() 夹角的最大值,并求此时
夹角的最大值,并求此时![]() 点的坐标
点的坐标
(3)判断函数![]() 的单调性,并用单调性的定义证明你的结论。
的单调性,并用单调性的定义证明你的结论。
23、已知曲线![]() ,过
,过![]() 上的点
上的点![]() 作曲线
作曲线![]() 的切线
的切线![]() 交
交![]() 轴于点
轴于点![]() ,再过点
,再过点![]() 作
作![]() 轴的平行线交曲线
轴的平行线交曲线![]() 于点
于点![]() ,再过点
,再过点![]() 作曲线
作曲线![]() 的切线
的切线![]() 交
交![]() 轴于点
轴于点![]() ,再过点
,再过点![]() 作
作![]() 轴的平行线交曲线
轴的平行线交曲线![]() 于点
于点![]() ,……,依次作下去,记点
,……,依次作下去,记点![]() 的横坐标为
的横坐标为![]()
![]()
(1)求数列![]() 的通项公式
的通项公式
(2)设数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:
,求证:![]()
(3)求证:![]()
参考答案:
一、选择题: ABDDDC ACDCBB
二、填空题: ![]() ;
; ![]() ; 35; 2;
; 35; 2; ![]() ;
;
![]()
三、解答题:
19、解:(1)![]()
![]()
![]() 函数
函数![]() 的单调增区间为
的单调增区间为![]()
(2)图象(略)
20、(1)![]() ,
,![]()
![]() ,
,![]() 猜想
猜想![]()
(2)![]() ,
,![]()
![]()
(1)当![]() ,即
,即![]() 时,函数
时,函数![]() 在区间
在区间![]() 上是减函数
上是减函数
![]() 当
当![]() 时,
时,![]() ,即
,即![]() ,该方程没有整数解
,该方程没有整数解
(2)当![]() ,即
,即![]() 时,
时,![]() ,解得
,解得![]() ,综上所述,
,综上所述,![]()
21、(1)连结![]() 交
交![]() 于
于![]() ,连结
,连结![]() ,
,![]() ,
,![]() ,又
,又![]() ,
,
![]() ,
,![]() ,即
,即![]() 平分
平分![]() ,
,![]() 是正三角形,
是正三角形,
![]() ,即
,即![]() ,
,![]() ,
,![]() ,
,![]()
(2)过![]() 作
作![]() 于
于![]() ,连结
,连结![]() ,设
,设![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() 就是直线
就是直线![]() 与平面
与平面![]() 所成的角。
所成的角。
![]() 是二面角
是二面角![]() 的平面角,
的平面角,![]() ,在
,在![]() 中,
中,
![]() ,
,![]() 直线
直线![]() 与平面
与平面![]() 所成角是
所成角是![]()
(3)![]() ,
,![]() 在平面
在平面![]() 外,
外,![]() ,
,![]() 点到面
点到面![]() 的距离即为点
的距离即为点![]() 到面
到面![]() 的距离,过点
的距离,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]() 的长即为点
的长即为点![]() 到面
到面![]() 的距离,菱形
的距离,菱形![]() 中,
中,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]()
22、解:(1)设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]()
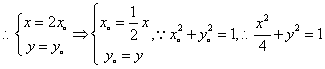
(2)设向量![]() 与
与![]() 的夹角为
的夹角为![]() ,则
,则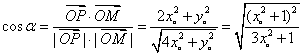
令![]() ,则
,则![]()
当且仅当![]() 时,即
时,即![]() 点坐标为
点坐标为![]() 时,等号成立。
时,等号成立。
![]() 与
与![]() 夹角的最大值是
夹角的最大值是![]()
23、解(1)![]() 曲线
曲线![]() 在点
在点![]() 处的切线
处的切线![]() 的斜率是
的斜率是![]() ,
,![]() 切线
切线![]() 的方程是
的方程是![]() ,由于点
,由于点![]() 的横坐标等于点
的横坐标等于点![]() 的横坐标
的横坐标![]() ,所以,令
,所以,令![]() ,
,
得![]() ,
,![]() 数列
数列![]() 是首项为1,公比为
是首项为1,公比为![]() 的等比数列,
的等比数列,![]()
(2)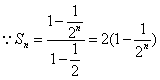 ,
,![]() ,令
,令![]() ,则
,则![]()
![]()
![]() 当
当![]() ,即
,即![]() 时,
时,![]() 有最大值1,即
有最大值1,即![]()
(3)![]() ,
,![]() ,即
,即![]() ,
,
![]() 数列
数列![]() 是首项为1,公比为4的等比数列
是首项为1,公比为4的等比数列
![]()