苏州中学高三数学综合训练(6)
班级 姓名 得分
一. 选择题:
1.将函数![]() 的图象按向量
的图象按向量![]() 平移后所得图象的解析式是 ( )
平移后所得图象的解析式是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2.已知![]() 是平面,
是平面,![]() 是直线.下列命题中不正确的是 ( )
是直线.下列命题中不正确的是 ( )
A.若![]() ,
,![]() ,则
,则![]() B.若
B.若![]() ,
,![]() ,则
,则![]()
C.若![]() ,
,![]() ,则
,则![]() D.若
D.若![]() ,
,![]() ,则
,则![]()
3.已知![]() ,则a+b的值所在的区间是 ( )
,则a+b的值所在的区间是 ( )
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
4.如图,A、B、C是表面积为48π的球面上三点,AB=2,BC=4,∠ABC=60°,O为球心,则直线OA与截面ABC所成的角等于 ( )
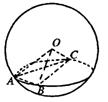 A.arcsin
A.arcsin![]() B.arccos
B.arccos![]()
C.arcsin![]() D.arccos
D.arccos![]()
5.互不相等的三个正数![]() 成等比数列,且点
成等比数列,且点
P1(![]()
![]() 共线
共线
![]() 则
则![]() ,
,![]() ( )
( )
A.等差数列,但不等比数列; B.等比数列而非等差数列
C.等比数列,也可能成等差数列 D.既不是等比数列,又不是等差数列
6.设实数![]() 满足
满足![]() ,
,![]() ,
,![]() ,则
,则![]() 与
与![]() 的大小关系为
( )
的大小关系为
( )
A.![]()
![]()
![]() B.
B.![]()
![]()
![]()
C.![]()
![]()
![]() D.不能确定,它们的大小与
D.不能确定,它们的大小与![]() 有关
有关
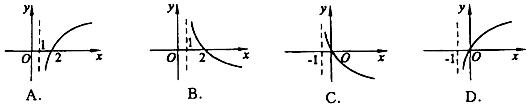 7.若函数
7.若函数![]() 既是奇函数,又是增函数,那么
既是奇函数,又是增函数,那么![]() 的图象是 ( )
的图象是 ( )
8.椭圆![]() 的长轴为A1A2,短轴为B1B2,将坐标平面沿y轴折成一个二面角,使点A1在平面B1A2B2上的射影恰是该椭圆的一个焦点,则此二面角的大小为
( )
的长轴为A1A2,短轴为B1B2,将坐标平面沿y轴折成一个二面角,使点A1在平面B1A2B2上的射影恰是该椭圆的一个焦点,则此二面角的大小为
( )
A.30° B.45° C.60° D.arctan2
9.已知![]() 的反函数为
的反函数为![]() ,则
( )
,则
( )
A. ![]() B.
B. ![]()
C .![]() D.
D. ![]()
10.一个机器人每一秒钟前进一步或后退一步,程序设计师设计的程序是让机器人以先前进3步,然后再后退2步的规律移动,如果将机器人放在数轴的原点,面向正的方向在数轴上移动(1步的距离为1个单位长度).令P(n)表示第n秒时机器人所在位置的坐标,且记P(0)=0,则下列结论中错误的是( )
A.P(3)=3 B.P(5)=1 C. P (2007)>P(2006) D.P(2003)<P(2006)
二、填空题:
11.已知实数x,y满足![]() ,则x的取值范围是 。
,则x的取值范围是 。
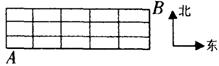 12.如图,小赵从A出发到达B处,他只知道
12.如图,小赵从A出发到达B处,他只知道
B在A的东北方向,图中一短线表示一段
道路,他每到一个交叉点路口时,对路线
作一次选择,每次都以概率p选择向东走,
以概率(1-p)选择向北走,经过8次选择可到达B处的概率是 .
13.在![]() 中,若
中,若![]() ,则
,则![]() ,
,
![]() 。
。
14.函数![]() 的定义域为 ;值域为 .
的定义域为 ;值域为 .
15.把座位编号分别为1,2,3,4,5,6的六张电影票全部分给甲、乙、丙、丁四个人,每人至少分1张,至多分两张,且分得两张票必须是连号的,那么不同的分法种数是 .
16.设函数f(x)的反函数为h(x),函数g(x)的反函数为h(x+1),已知f(2)=5,f(5)=-2,f(-2)=8,那么g(2)、g(5)、g(8)、g(-2)中,一定能求出具体数值的是 .
三.解答题:
17.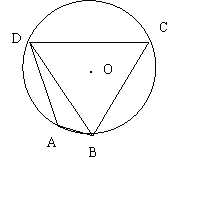 如图圆内接四边形ABCD中,
如图圆内接四边形ABCD中,![]() =
=![]() ,
,![]() ,
,
圆的半径是![]() ,O是圆心 。
,O是圆心 。
(1)求角![]() 和
和![]()
(2)求![]()
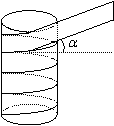 18.水管或煤气管经常需要从外部包扎以便对管道起保护作用.包扎时用很长的带子缠绕在管道外部(如图所示).假定为了节省材料,包扎时要使带子全部包住管道而且带子没有重叠的部分,这就要精确地计算带子的缠绕角度a(如图所示).
18.水管或煤气管经常需要从外部包扎以便对管道起保护作用.包扎时用很长的带子缠绕在管道外部(如图所示).假定为了节省材料,包扎时要使带子全部包住管道而且带子没有重叠的部分,这就要精确地计算带子的缠绕角度a(如图所示).
(1) 包扎时带子的缠绕角度a与哪些量有关?
(2) 用字母表示出上述有关的量,并用它们表示出缠绕角a.
19.如图,正方形A1BA2C的边长为4,D是A1B的中点,E是BA2上的点,将△A1DC及△A2EC分别沿DC和EC折起,使A1A2重合于A,且二面角A—DC—E为直二面角。
(1) 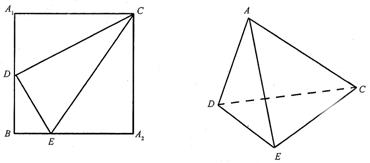 求证:CD⊥DE;
求证:CD⊥DE;
(2) 求AE与面DEC所成角的正弦值;
(3) 求点D到平面AEC的距离。
20. 已知抛物线C的顶点在原点,以双曲线![]() 的左准线为准线,
的左准线为准线,
(1)求抛物线C的方程;
(2)A是抛物线C上任一点,A关于x轴的对称点为B,过A作抛物线的弦AP、AQ,且AP⊥AQ,是否存在常数h,使得![]() ?
?
21.数列![]() 的各项均为正值,
的各项均为正值,![]() ,对任意
,对任意![]() ,
,![]() ,
,![]() 都成立.
都成立.
(Ⅰ)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(Ⅱ)当![]() 且
且![]() 时,证明对任意
时,证明对任意![]() 都有
都有![]() 成立.
成立.
苏州中学高三数学综合训练(6)答案
一、选择题:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| A | B | C | D | C | C | D | A | B | D |
二、填空题:
11.![]() 12. 56p5(1-p)3 13.6 : 2 : 3;
12. 56p5(1-p)3 13.6 : 2 : 3;![]()
14.![]() ;
;![]() 15.144 16.g(2),g(5),g(-2)
15.144 16.g(2),g(5),g(-2)
解析:由h(x)=f-1(x), h(x+1)=g-1(x), ∴g-1(x)=f-1(x+1)=y, 即x=g(y),x+1=f(y). ∴g(x)=f(x)-1.
∴g(2)=f(2)-1=4,g(5)=-3,g(-2)=7.
三、解答题:
17.解:(1)由正弦定理![]() ,得
,得![]() ,又由题意知
,又由题意知
![]() 是锐角,∴
是锐角,∴![]()
由余弦定理![]() 得
得![]()
显然![]() 是锐角,∴
是锐角,∴![]() ,又圆心角
,又圆心角![]()
∴![]()
(2)易见三角形BCD是正三角形 ∴![]()
∴![]()
![]()
![]()
![]()
18.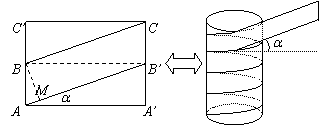 解 (1)缠绕角a显然与管子的直径、带子的宽度有关.
解 (1)缠绕角a显然与管子的直径、带子的宽度有关.
(2) 设管子的直径为D,带子的宽度为W.
把管子看作圆柱体,设想将侧面沿某一母线剪开后展开,其展开图如图所示.由题意,包扎时要使带子全部包住管道而且带子没有重叠的部分,这就意味着点B与B¢必在同一水平线上.
过点B作BM^AB¢,M为垂足,则BM=W;同时,AA¢=pD,∠A¢AB¢=a.
\在RtΔBMB¢中,sin a=BM:BB¢=W:pD
\![]()
解: 19.(1)∵A1、A2重合于A
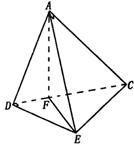 ∴AC⊥AD,AC⊥AE,故AC⊥面ADE ∴AC⊥DE
∴AC⊥AD,AC⊥AE,故AC⊥面ADE ∴AC⊥DE
∵A-DC-E为直二面角, ∴过A作AF⊥CD于F,则AF⊥面CDE,
故CD为AC在面CDE上的射影,由三垂线定理的逆定理有:CD⊥DE.
(2)∵AF⊥面CDE,∴∠AEF为AE与面DEC所成的角,
在Rt△CAD中,AD=2,AC=4,∴DC=2![]() ,AF=
,AF=![]() ,
,
又∵CD⊥DE,∴在正方形A1BA2C中,△DBE~△CA1D
故![]() ,∴DE=
,∴DE=![]() 又∵DE⊥CD,DE⊥AC,∴DE⊥面ACD,则
又∵DE⊥CD,DE⊥AC,∴DE⊥面ACD,则
DE⊥AD,∴在Rt△ADE中,AE=3,故在Rt△AFE中,![]() ∴AE与面DEC所成角的正弦值为
∴AE与面DEC所成角的正弦值为![]() .
.
(3)设D到面AEC的距离为d,则由VD—AEC=VA—DEC有:![]()
∴3×4d=2![]() 故
故![]() ,即点D到平面AEC的距离为
,即点D到平面AEC的距离为![]() .
.
20.解:(1)双曲线的左准线为x=-1,![]() 抛物线方程是
抛物线方程是![]() ;
;
(2)设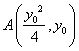 ,AP的直线方程为
,AP的直线方程为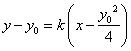 ,
,
将抛物线方程![]() 代入AP的直线方程,得
代入AP的直线方程,得![]() ,
,
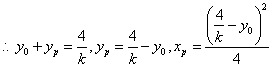 ,
,
同理:![]() ,
,
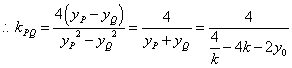 ,
,
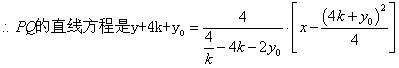 ,
,
令![]() ,
,
![]()
![]() 点的坐标是
点的坐标是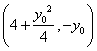 ,
,
∴存在h=4,使得![]() 且
且![]()
21.解:由![]() 得,
得,
![]()
数列![]() 的各项为正值,
的各项为正值,![]()
![]()
![]()
又![]()
∴数列![]() 为等比数列. ∴
为等比数列. ∴![]() ,
, ![]() ,
,
![]()
(2)设![]()
∴![]() (1)
(1)
当![]() 时,
时,![]() ,
,![]()
∴![]() ,
,![]() , 当且仅当
, 当且仅当![]() 时等号成立.
时等号成立.
上述(1)式中,![]() ,
,![]() ,
,![]() 全为正,所以
全为正,所以
![]()
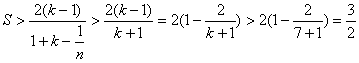
得证.