英山一中2007届高三8月月考试题
时间:2006.8.20
一、选择题:本大题共10小题,每小题5分,共50分.
1.命题“若![]() ,则
,则![]() ”的否命题是
( )
”的否命题是
( )
A.若![]() ,则
,则![]() B.若
B.若![]() ,则
,则![]()
C.若![]() ,则
,则![]() D.若
D.若![]() ,则
,则![]()
2.若![]() ,则下列结论不正确的是
( )
,则下列结论不正确的是
( )
![]()
![]()
![]()
![]()
3. 已知函数y=f(n),(n![]() N*),如果7f(n)=f(n-1),f (1)=3,则
N*),如果7f(n)=f(n-1),f (1)=3,则![]() [f(1)+f(2)+…+f(n)]=( )
[f(1)+f(2)+…+f(n)]=( )
A.0 B.![]() C.
C.![]() D.3
D.3
4.已知l,m,表示直线,![]() 表示平面,下列条件中能推出结论的正确的是( )
表示平面,下列条件中能推出结论的正确的是( )
条件:①l⊥m,l⊥![]() ,m⊥
,m⊥![]() ②
②![]() ∥
∥![]() ,
,![]() ∥
∥![]() ③l⊥
③l⊥![]() ,
,![]() ∥
∥![]() ; ④ l⊥
; ④ l⊥![]() ,m⊥
,m⊥![]()
结论:a: l ⊥![]() b:
b: ![]() ⊥
⊥![]() c: l∥m d:
c: l∥m d: ![]() ∥
∥![]()
A ①![]() a,②
a,②![]() b,③
b,③![]() c,④
c,④![]() d
B ①
d
B ①![]() b,②
b,②![]() d,③
d,③![]() a,④
a,④![]() c
c
C ①![]() c,②
c,②![]() d,③
d,③![]() a,④
a,④![]() b
D ①
b
D ①![]() d,②
d,②![]() b,③
b,③![]() a,④
a,④![]() c
c
5. 当n∈N且n≥2时,1+2+22+…+24n-1=5p+q,其中p,q为非负整数,且0≤q<5,则q的值为 ( )
A.0 B.2 C.2 D.与n有关
6. 已知数列{an}中,a1=8, a2 =4且满足an+1-2an+ an-1=0(n∈N*,n≥2),则数列{an}的前
30项的绝对值的和为( )
(A)870 (B)830 (C)1524 (D)1512
|
|
|
|
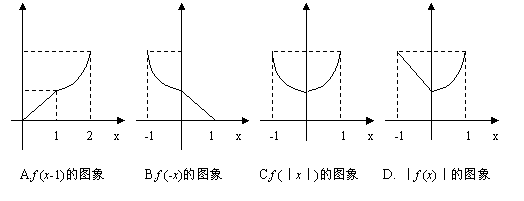 7.已知
7.已知
8定义运算![]()
![]() ,若复数
,若复数![]() ,
,![]()
![]() ,则
,则![]() ( )
( )
A. -4 B.4 C.2 D.-2
9.如果 (sinx) ′=cosx , (cosx) ′=-sinx,设 f0(x)=sinx,f1(x)=f0′(x),f2(x)=f1′(x),…,fn+1(x)=fn′(x),n∈N,则f2006(x)= ( )
A.sinx B.-sinx C.cosx D.-cosx
10. 已知点A(1,0),B(1,![]() ),将线段OA, AB 均n等分,设OA 上从左至右的第k个分点为Ak, AB上从下至上的第k个分点为Bk(1≤k≤n),过点Ak,且垂直于x轴的直线为lk,OBk交lk于点Pk在同一 ( )
),将线段OA, AB 均n等分,设OA 上从左至右的第k个分点为Ak, AB上从下至上的第k个分点为Bk(1≤k≤n),过点Ak,且垂直于x轴的直线为lk,OBk交lk于点Pk在同一 ( )
A圆上 B椭圆上 C双曲线上 D抛物线上
二、填空题:本大题共5小题,每小题5分,共25分.
11.已知集合![]() ,若
,若![]() ,则a 的取值范围为
.
,则a 的取值范围为
.
12.对于正整数![]() 和
和![]() ,定义
,定义![]() !=
!=![]() ,其中
,其中![]() ,且
,且![]() 是满足
是满足![]() 的最大整数,则(
的最大整数,则(![]() !)/(10
!)/(10![]() !)=___________
!)=___________
13.设正数数列{ an}为等比数列,且a2=4,a4=16,则![]()
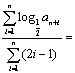
14.对于长和宽分别是2和1的矩形来说,总存在另外一个矩形,它的周长和面积都是已知矩形的m倍,则m的取值范围是________
15.对于任意实数x
, y ,定义运算![]() ,其中a,
b, c为常数,等号右边的运算是通常意义的加、乘运算.现已知1*2=3, 2*3=4,且有一个非零的实数m,使得对任意实数x,都有x*
m=x,则m=
.
,其中a,
b, c为常数,等号右边的运算是通常意义的加、乘运算.现已知1*2=3, 2*3=4,且有一个非零的实数m,使得对任意实数x,都有x*
m=x,则m=
.
三、解答题:本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.
16.(本小题满分12分)
若方程![]() (其中
(其中![]() 的两实根为α、β,数列1,
的两实根为α、β,数列1,
![]() ,(
,(![]() ,……的所有项的和为2-
,……的所有项的和为2-![]() ,试求θ的值。
,试求θ的值。
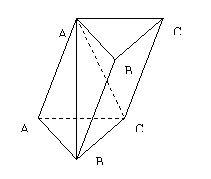 17. 在三棱柱ABC—A1B1C1中,A1B1是A1C和B1C1的公垂线段,A1B与平面ABC成60°角,AB=
17. 在三棱柱ABC—A1B1C1中,A1B1是A1C和B1C1的公垂线段,A1B与平面ABC成60°角,AB=![]() ,A1A=AC=2
,A1A=AC=2![]()
(1)求证:AB⊥平面A1BC;
(2)求A1到平面ABC的距离;
(3)求二面角A1—AC—B的大小.
18.(12分)某种比赛的规则是5局3胜制,甲乙两人在比赛中获胜的概率分别是![]() 和
和![]() 。 (1)若前三局中乙以2:1领先,已成定局,求乙获胜的概率。
。 (1)若前三局中乙以2:1领先,已成定局,求乙获胜的概率。
(2)若胜一局得2分,负一局得-1分,求甲得分![]() 的数学期望。
的数学期望。
19. (12分)设函数f(x)=-![]() x3+2ax2-3a2x+
x3+2ax2-3a2x+![]() a(0<a<1)
a(0<a<1)
(1) 求函数f(x)的单调区间
(2)
若当x![]() [a, 2]时,恒有f(x)≤0,试确定a的取值范围
[a, 2]时,恒有f(x)≤0,试确定a的取值范围
20.(13分)已知点A(1,0),B(0,1),C(1,1)和动点P(x,y)满足![]() 的等差中项. (1)求P点的轨迹方程;
的等差中项. (1)求P点的轨迹方程;
(2)设P点的轨迹为曲线C1按向量![]() 平移后得到曲线C2,曲线C2上不同的两点M,N的连线交y轴于点Q(0,b),如果∠MON(O为坐标原点)为锐角,求实数b的取值范围;
平移后得到曲线C2,曲线C2上不同的两点M,N的连线交y轴于点Q(0,b),如果∠MON(O为坐标原点)为锐角,求实数b的取值范围;
(3)在(2)的条件下,如果b=2时,曲线C2在点M和N处的切线的交点为R,求证:R在一条定直线上.
21.(14分)已知二次函数![]() 的图象过点
的图象过点![]() ,且
,且![]()
(1)求![]() 的解析式;
的解析式;
(2)若数列![]() 满足
满足![]() ,且
,且![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(3)对于(2)中的数列![]() ,求证:①
,求证:①![]() ;②
;②![]() 。
。
答案
CCBBA CDBBD 11.(-![]() ,+∞); 12、
,+∞); 12、![]() ;
13.
;
13.![]() ; 14. [
; 14. [![]() , +
, +![]() ] 15.4
] 15.4
16.解:
![]() 、
、![]() 是方程
是方程![]() 的两实根
的两实根
![]() (1)
(1) ![]() ……4分
……4分
![]()
由已知![]() 而
而![]()
![]() ……
……![]()
![]()
![]() 满足(2)
满足(2) ![]() 不满足(1)故
不满足(1)故![]() ……12分
……12分
17.解(1)∵三棱柱ABC—A1B1C1中A1B1是A1C与B1C1的公垂线段,A1C1⊥B1C1
AB⊥BC,AB⊥A1C又A1C∩A1B=A1 ∴AB⊥平面A1BC…………………4分
(2)∵AB![]() 平面ABC,AB⊥平面A1BC ∴面ABC⊥面A1BC作A1O⊥BC垂足为O,则A1O⊥平面ABC … 6分 ∠A1BC为A1B与平面ABC所成角即∠A1BC=60°在Rt△A1AB中, A1B=
平面ABC,AB⊥平面A1BC ∴面ABC⊥面A1BC作A1O⊥BC垂足为O,则A1O⊥平面ABC … 6分 ∠A1BC为A1B与平面ABC所成角即∠A1BC=60°在Rt△A1AB中, A1B=![]()
![]() 即A1到平面ABC的距离为
即A1到平面ABC的距离为![]()
(3) 由O引垂线OH⊥AC垂足为H,连接A1H由三垂线定理可证AC⊥A1H
∴∠A1HO为二面角A1—AC—B平面角 ………………………11分
在△ABC中解得OH=![]() ,在△OA1H中解得
,在△OA1H中解得![]()
∴二面角A1—AC—B大小为![]() ………………14分
………………14分
18解:(1)在以后的比赛中,
乙胜一场或两场都胜, 故乙获胜的概率P1=C![]() ×
×![]() ×
×![]() +(
+(![]() )2=
)2=![]()
(2)![]() =6,表示甲连续胜三场P(
=6,表示甲连续胜三场P(![]() =6)=(
=6)=(![]() )3=
)3=![]()
![]() =5 表示甲以3:1胜,P(
=5 表示甲以3:1胜,P(![]() =5)=C
=5)=C![]() (
(![]() )2×
)2×![]() ×
×![]() =
=![]()
![]() =4,表示甲以3:2胜利,P(
=4,表示甲以3:2胜利,P(![]() =4)=C
=4)=C![]() (
(![]() )2×(
)2×(![]() )2×
)2×![]() =
=![]()
![]() =1,表示甲以2:3失败,P(
=1,表示甲以2:3失败,P(![]() =1)= C
=1)= C![]() (
(![]() )2×(
)2×(![]() )2×
)2×![]() =
=![]()
![]() =-1,表示甲以1:3失败,P(
=-1,表示甲以1:3失败,P(![]() =-1)=C
=-1)=C![]()
![]() ×(
×(![]() )2×
)2×![]() =
=![]()
![]() =-3,表示甲以0:3失败,P(
=-3,表示甲以0:3失败,P(![]() =-3)=(
=-3)=(![]() )3=
)3=![]()
E![]() =6×
=6×![]() +5×
+5×![]() +4×
+4×![]() +1×
+1×![]() -1×
-1×![]() -3×
-3×![]() =
=![]()
19![]() 20.解:(1)f’(x)=-x2+4ax-3a2=-(x-a)(x-3a)
20.解:(1)f’(x)=-x2+4ax-3a2=-(x-a)(x-3a)
因为0<a<1,所以,f’(x)>0![]() a<x<3a
a<x<3a
f’(x)<0![]() x<a或x>3a
x<a或x>3a
所以递增区间为(a,3a);递减区间为(3a,+![]() ),(-
),(-![]() ,a)
,a)
(2)∵x![]() [a, 2]
[a, 2]
∴①当2≤3a,即![]() ≤a<1时,f(x)在区间[0,2]内是增函数。
≤a<1时,f(x)在区间[0,2]内是增函数。
∴f(x)max=f(2)=-![]() +
+![]() a-6a2
a-6a2
∴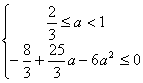
![]()
![]()
②当2>3a即0<a<![]() 时,f(x)max=f(3a)=
时,f(x)max=f(3a)=![]() a
a
∴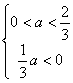 无解。综上所述,a的取值范围是
无解。综上所述,a的取值范围是![]()
20.(1)由题意可得![]() 则
则
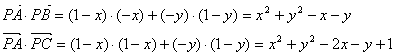
又![]() 的等差中项
的等差中项
![]()
整理得点![]() 的轨迹方程为
的轨迹方程为![]() ……………………………4分
……………………………4分
(2)由(1)知![]()
又![]() 平移公式为
平移公式为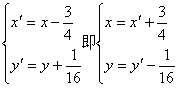 ,代入曲线C1的方程得到曲线C2的方程为:
,代入曲线C1的方程得到曲线C2的方程为:![]()
即![]() ………………………………………………… 6分
………………………………………………… 6分
曲线C2的方程为![]() . 如图由题意可设M,N所在的直线方程为
. 如图由题意可设M,N所在的直线方程为![]() ,
,
由 令
令
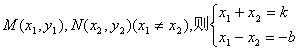 ………………………8分
………………………8分
点M,N在抛物线上![]()
![]()
又![]() 为锐角
为锐角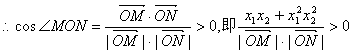
![]() ………10分
………10分
(3)当b=2时,由(2)可得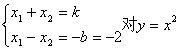 求导可得
求导可得![]()
![]() 抛物线C2在点
抛物线C2在点![]() 处的切线的斜率分别为
处的切线的斜率分别为![]() ,
,
![]() 在点M、N处的切线方程分别为
在点M、N处的切线方程分别为
![]()
由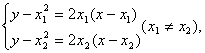 解得交点R的坐标
解得交点R的坐标![]()
满足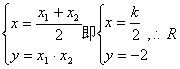 点在定直线
点在定直线![]() 上……………………15分
上……………………15分
21.(1)![]() ;
;
(2)![]() ;
;
(3)①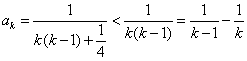 (
(![]() )
)
当![]() 时,显然成立;
时,显然成立;
当![]() 时,
时,![]() ;
;
②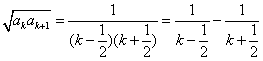 ,
,
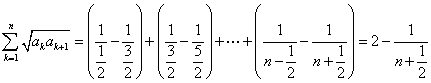 ,所以不等式成立
,所以不等式成立