黄冈市重点中学2006届高三(十一月)联考
数学试题 (理科)
一.选择题(每小题5分,共60分)
1.已知集合![]()
![]() ,则
,则![]() =( )
=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.“![]() ”是“
”是“![]() ”的
( )
”的
( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
3.已知![]() ,
,![]() ,则
,则![]() 所在的象限为
( )
所在的象限为
( )
A.第四象限 B.第三象限 C.第二象限 D.第一象限
4.等比数列![]() 的各项均为正数,
的各项均为正数,![]() ,则
,则![]() 的值为
( )
的值为
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.已知![]() ,则
,则![]() 的值为
( )
的值为
( )
A.![]() B.
B. ![]() C.
C.![]() D.
D.![]()
6.![]() 为平面内的动点,A、B、C是平面内不共线的三点,满足
为平面内的动点,A、B、C是平面内不共线的三点,满足![]() ,则
,则![]() 点轨迹必过的
( )
点轨迹必过的
( )
A.垂心 B.外心 C.重心 D.内心
7.设函数若对于任意,均有成立,则的最小值为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.命题![]() :函数
:函数![]() 的值域为
的值域为![]() ,则
,则![]() ;
;
命题![]() :函数
:函数![]() 的定义域为
的定义域为![]() ,则 ( )
,则 ( )
A.“![]() 或
或![]() ”为假 B.“
”为假 B.“![]() 且
且![]() ”为真 C.
”为真 C.![]() 真
真![]() 假 D.
假 D.![]() 假
假![]() 真
真
9.如图所示,有一广告气球,直径为6m,放在公司大楼上空,当行人仰望气球中心的仰角![]() 时,测得气球的视角
时,测得气球的视角![]() ,若
,若![]() 很小时可取
很小时可取![]() ,试估算该气球离地高度BC的值约为( )
,试估算该气球离地高度BC的值约为( )
A.72m B.86m C.102m D.118m
10.在![]() 中,若
中,若![]() ,
,![]() ,则角C的大小为( )
,则角C的大小为( )
A.![]() B.
B.![]() C.
C.![]() 或
或![]() D.
D.![]() 或
或![]()
11.设![]() 若
若![]() 、
、![]() ,且
,且![]() 则下列结论成立的是( )
则下列结论成立的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.2003年3月,全世界爆发“非典”,科学家经过深入的研究,终于发现了一种细菌M在杀死“非典”病毒N的同时能够自身复制,已知1个M可以杀死一个病毒N,并且生成2个细菌M,那么1个细菌M和2048个“非典”病毒N最多可生成细菌M的数值是( )
A.1024 B.2048 C.2049 D.无法确定
选择题答题卡:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题:(每小题4分,共16分)
13.定义运算![]() ※
※![]() ,则函数
,则函数![]() ※
※![]() 的最大值为
。
的最大值为
。
14.设![]() ,
,![]() ,
,![]() 则a、b、c 大小关系为
。
则a、b、c 大小关系为
。
15已知函数![]() 的图象沿
的图象沿![]() 轴方向向左平移1个单位后与
轴方向向左平移1个单位后与![]() 的图象关于直线
的图象关于直线![]() 对称,且
对称,且![]() ,则函数
,则函数![]() 的值域为
。
的值域为
。
16.计算机执行以下程序:
①初始值![]() ;
;
②![]() ;
;
③![]() ;
;
④如果![]() ,则进行⑤,否则从②继续运行;
,则进行⑤,否则从②继续运行;
⑤打印![]() ;
;
⑥![]() 。
。
那么由语句⑤打印出的数值为 。
三、解答题:(共6小题,74分,解答题应写出文字说明,证明过程及演算步骤)
17、(12分)已知![]() ,
,![]()
![]() 。
。
(1)求![]() 。 (2)求
。 (2)求![]() 的值。
的值。
18、(12分)数列![]() 对所有正整数
对所有正整数![]() ,满足:
,满足:
![]() 。
。
(1)求![]() 及
及![]()
(2)当![]() 时,设
时,设![]() ,求
,求![]()
19、(12分)已知锐角![]() 中,角
中,角![]() 、
、![]() 、
、![]() 的对边分别为
的对边分别为![]() 、
、![]() 、
、![]() ,且
,且![]() 。
。
(1)求![]() ;
(2)求
;
(2)求![]() 。
。
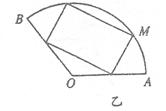
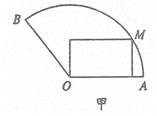 20、(12分)将一块圆心角为
20、(12分)将一块圆心角为![]() ,半径为
,半径为![]() 的扇形的铁片截成一块矩形,如图,有2种裁法:让矩形一边在扇形的一半径OA上或让矩形一边与弦
的扇形的铁片截成一块矩形,如图,有2种裁法:让矩形一边在扇形的一半径OA上或让矩形一边与弦![]() 平行,请问哪种裁法能得到最大面积的矩形,并求出这个最大值。
平行,请问哪种裁法能得到最大面积的矩形,并求出这个最大值。
 |
21、(12分)已知![]() ,函数
,函数![]() 在
在![]() 上是单调函数。
上是单调函数。
①求函数![]() 的最小值。
的最小值。
②设![]() 且
且![]() ,求证:
,求证:![]()
22、(14分)设函数![]() 是定义在
是定义在![]() 上的函数,当
上的函数,当![]() 时,
时,![]() ,对任意实数
,对任意实数![]() 、
、![]() ,有
,有![]()
(I)求证:![]() 且当
且当![]() 时,有
时,有![]()
(II)若数列![]() 满足
满足![]() ,且
,且![]() ,
,![]()
①求![]() ;
;
②若不等式![]() 对于
对于![]() 都成立,求
都成立,求![]() 的最大值。
的最大值。
数学试题(理科)答案
一、选择题答题卡:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | D | A | B | A | C | B | D | B | A | D | C |
二、填空题答题卡:
13. ![]() 14. a<c<b
14. a<c<b
15. ![]() 16. 23
16. 23
三、解答题:(共6小题,74分,解答题应写出文字说明,证明过程及演算步骤)
17、
解:(1)设![]()
(2)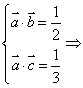
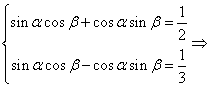
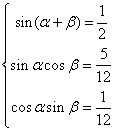
![]() 原式
原式![]()
18、
解:(1)当![]() 时,
时,![]()
当![]() 时,
时,![]()
![]()
![]() 当
当![]() ,
,![]() 即
即![]()
故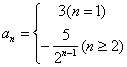
(2)![]()
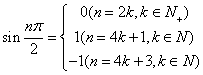
![]()
![]()
![]()
![]()
![]() =
=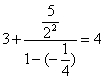
19、
解:(1)![]() (2)原式=
(2)原式=![]()
![]() =
=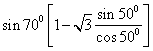
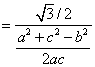 =
=![]()
=![]() =
=![]()
![]() =
=![]()
![]() =
=![]()
![]() 在锐角
在锐角![]() 中
中![]()
20、解:在甲图中:连结OM,设![]()
![]() S矩=
S矩=![]()
![]() 当
当![]() 时
S矩/max=
时
S矩/max=![]()
在乙图中,同理连结MO,设![]() 则由
则由![]() 可知:
可知:
![]()
![]()
![]() =
=![]()
同理![]() 又在
又在![]() 中,CD=
中,CD=![]()
![]()
![]() 矩
矩![]()
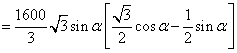
![]()
![]() 当
当![]() 时S’矩/max
时S’矩/max![]()
故乙方案裁法能得到最大面积矩形,最大值为![]()
21、
解:①![]()
![]()
由![]() ,即
,即![]()
但![]() 对
对![]() 不可能恒成立
不可能恒成立
![]() 对
对![]() 不可能恒成立
不可能恒成立
![]() 在
在![]() 不能单调递减,只能单增
不能单调递减,只能单增
又由![]() ,得
,得![]() ,对
,对![]() 恒成立,
恒成立,![]()
![]()
又![]()
![]()
![]()
![]() 在
在![]() 单增 且
单增 且 ![]() 而
而![]()
![]() 当且仅当
当且仅当![]() ,即
,即![]() 时,
时,![]()
证②:设![]() ,则
,则![]()
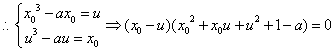
![]() ,且
,且![]()
![]()
![]()
![]() ,即
,即![]() 故
故![]()
注:①可用定义法 ②可用反证法
22、
证(I):![]() 、
、![]() 有
有![]()
![]() 取
取![]() 则
则![]()
![]() 时
时![]()
![]()
又设![]() 则
则![]()
![]()
![]()
而当![]() 时,
时,![]()
![]() 当
当![]() 时
时 ![]()
(II):①![]()
由![]() 得
得![]()
![]()
![]()
可证![]() 是R的递减函数,证明如下:
是R的递减函数,证明如下:
设![]() 、
、![]() 且
且![]() 则
则![]()
![]()
即![]()
![]() 是
是![]()
![]() 即
即![]()
![]()
②设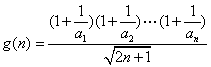 ,得
,得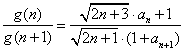
![]()
![]()
![]() 即
即![]()
![]() 对
对![]() 单增
单增
而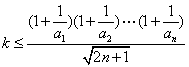 即
即![]() 对
对![]() 恒成立
恒成立
![]() 即
即![]()