2006年温州市高三第二次适应性测试
数学（文科）试卷 2006.4
注意事项：
本试卷分为第Ⅰ卷（选择题）第Ⅱ卷（非选择题）两部分，共8页，满分为150分，考试时间为120分钟。
| 参考公式：如果事件A、B互斥，那么 | 球的表面积公式 |
| P(A+B)=P(A)+P(B) | S=4 |
| 如果事件A、B相互独立，那么 | 其中R表示球的半径 |
| P(A•B)=P(A)•P(B) | 球的体积公式 |
| 如果事件A在一次试验中发生的概率是P， 那么n次独立重复试验中恰好发生k次的概率 |
|
|
| 其中R表示球的半径 |
R2
一、选择题：（本大题共10小题, 每小题5分, 共50分. 在每小题给出的四个选项中, 有且只有一项是符合题目要求的，请将答案填写在答卷纸上）
1．
是
成立的( )条件
A．充分不必要 B．必要不充分 C．充要 D．既不充分也不必要
|
B．
C．9 D．
，则
( )
3．抛物线
的焦点也是椭圆
的一个焦点，则
( )
A．
B．
C．4
D．
4．已知
，则满足条件的集合
的个数为 ( )
A．2 B．3 C．4 D．7
5．点O是ΔABC所在平面内一点，且满足
，则点O必在 ( )
A．边AC的垂直平分线上 B．边AC的中线所在的直线上
C．边AC的高所在直线上 D．
的内角平分线所在的直线上
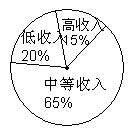
6．2005年底，某地区经济调查队对本地区居民收入情况进行抽样调查，抽取1000户，按
|
本地区在“十一五”规划中明确
提出要缩小贫富差距，到2010年
要实现一个美好的愿景，由右边圆图显示，则中等收入家庭的数
量在原有的基础要增加的百分比和低收入家庭的数量在原有的基
础要降低的百分比分别为 ( )
A．25% , 27.5% B．62.5% , 57.9% C．25% , 57.9% D．62.5%,42.1%
7．某学校要从10位优秀学生中选出6位参加全市研究性学习成果汇报会，其中甲、乙两位学生不同时入选，则不同的选法总数是( )
A．84 B．98 C．112 D．140
8．已知直线
，平面
，则下列命题正确的是 ( )
A．
B．
C．
D．
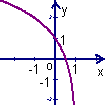
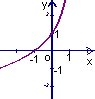
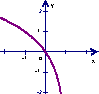
9．已知函数
的反函数是
，则函数
的图象是 ( )
 | |||||||
 | |||||||
 | |||||||
 | |||||||
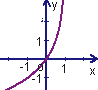A B C D
10．已知函数
的最小正周期为
，且为偶函数
则
的一个递减区间为
(
)
A．
B．
C．
D．
二、填空题：（本大题共4小题，每小题4分，共16分.把答案填在答题卷上）
11．
，则
▲
12．已知
，
若
，则
的取值范围是 ▲ 。
13．把一个体积为
的球放在一个正三棱柱的盒子里，这个球面恰好与这正三棱柱的所有面都相切，则这正三棱柱的底面边长为 ▲ 。
14．已知点
是由四条直线
所围成的矩形区域（包括边界）内的动点，则动点
形成的平面区域的面积为 ▲ 。
2006年温州市高三第二次适应性测试
数学（文科）答卷纸 2006.4
| 题号 | 一 | 二 | 三 | 总分 | |||||
| 15 | 16 | 17 | 18 | 19 | 20 | ||||
|
| |||||||||
得分一、选择题（本大题共10个小题，每小题5分，共50分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 总分 |
| 答案 |
|
填在题中横线上）
11． 12．
13． 14．
三、解答题（本大题共6个小题，共84分，解答应写出文字说明，证明过程或演算步骤）
|
已知
分别为
的角A、B、C的对应边，
且
∥
，
（Ⅰ）求：角
的大小；
（Ⅱ）若
，且
，求
的值。
|
已知等比数列
中，公比
，且
是
与
的等差中项，
前
项和为
，数列
满足：
（Ⅰ）若
，求数列的前项的和
；
（Ⅱ）若
＋
＝
，求的值。
|
甲、乙两人进行两种游戏，两种游戏的规则由下表给出：
（球的大小都相同）
| 游戏1 | 游戏2 |
| 裁判的口袋中有4个白球和5个红球 | 甲的口袋中有6个白球和2个红球 乙的口袋中有3个白球和5个红球 |
| 由裁判摸两次，每次摸一个，记下颜色后放回 | 每人都从自己的口袋中摸一个球 |
| 摸出的两球同色→甲胜 摸出的两球不同色→乙胜 | 摸出的两球同色→甲胜 摸出的两球不同色→乙胜 |
（Ⅰ）分别求出在游戏1中甲、乙获胜的概率；
（Ⅱ）求出在游戏2中甲获胜的概率，并说明这两种游戏哪种游戏更公平。
|
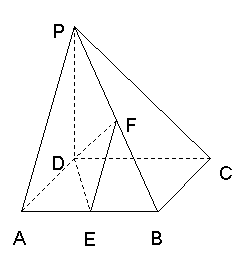
如图：在四棱锥
中，
⊥底面
，
底面为正方形，
分别是
的中点，
（Ⅰ）求证：
⊥
；
（Ⅱ）求面
与面
所成二面角的大小；（用反三角表示）
 |
|
已知函数
的定义域为
，
（Ⅰ）当
时，若函数的导数
满足关系
，求
的取值范围；
（Ⅱ）若函数
同时满足以下两个条件：①函数在
上单调递增；②函数，
的图象的最高点落在直线
上，求
的值。
|
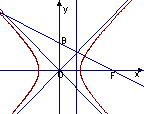
已知点A、F分别为双曲线C：
的右顶点、右焦点，点B的坐标为
，且
（其中O为坐标原点）．
（Ⅰ）求双曲线C的离心率；
（Ⅱ）求证：三条直线
、双曲线C的渐近线
、右准线交于一点；
（Ⅲ）是否存在直线
经过点F，与双曲线C的右支交于点Ｐ，与
轴交于点Q，使点Ｐ恰是线段FQ的中点，若存在，求出直线的斜率，若不存在，请说明理由。
2006年温州市高三第二次适应性模拟测试
数学（文科）参考答案与评分标准 2006.4
一、选择题（本大题共10小题, 每小题5分, 共50分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | A | B | A | C | Ｃ | Ｂ | Ｄ | Ｂ | Ａ | Ｄ |
二、填空题（本大题共4小题，每小题4分，共16分.把答案填在题中横线上）
11． ０ 12．
13．． 14．16
三、解答题（本大题共6个小题，共84分，解答应写出文字说明，证明过程或演算步骤）
15．解：（Ⅰ）
…5分
…７分
（Ⅱ）
………９分
或
，
，
………12分
又
（由正弦定理得）………14分
16.（Ⅰ）解：因为是与的等差中项，
……３分
或
，因为，所以
………５分
………８分
（Ⅱ）解：
，
又
所以，
∴ｋ＝２………14分
解：（Ⅰ）有放回的取球就是独立重复试验，裁判取出两球都是白球为事件A，都是红球为事件B，A、B为互斥事件，
,即甲获胜的概率为
……5分，因为乙获胜是甲获胜的对立事件，所以乙获胜的概率为
。…7分
（Ⅱ）设甲摸出白球且乙也摸出白球为事件C，甲摸出红球且乙也摸出红球为事件D， C、D 为
互斥事件
。
∴甲获胜的概率为
……12分 。因为和比和
更接近
，所以游戏1更公平。（也可以看这两个对立事件的概率差的绝对值哪个小哪个就更公平）……14分
18．（Ⅰ）证明：因为
分别是的中点，
所以
，为正方形
⊥底面，
平面
……6分
证法二：分别以直线
为x轴，y轴，z轴
建立空间直角坐标系
，
………６分
（Ⅱ）解：过点F作
为垂足，过H作
为垂足，连接
，
⊥底面，
………８分
。………９分
………12分
即为所求的二面角的平面角。………14分
解法二：设：
为平面
的一个法向量，
，…８分
取
，………12分
取平面的法向量
，设：面与面所成二面角为
，
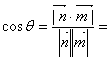
………14分
19．解：（Ⅰ）=
或
且
，………４分
或
，所以的取值范围为：
…………６分
（Ⅱ）=
，
当
时，
，因为函数在上单调递增，所以
，
，………９分
当
时，
在上恒有
，所以函数在上为增函数
，舍去。………11分
当
时，
，在
上和在
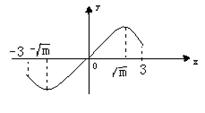
都单调递减，在
单调递增，所以在上
………14分
20．（Ⅰ）解：因为
即：
………6分
(Ⅱ) 解：直线：
与渐近线
的交点
………8分
所以在右准线上，
即直线、渐近线、右准线交于一点。………10分
（Ⅲ）若直线存在，设直线的斜率为，直线
，则
………11分
点P在双曲线C上，
，
而
，故
，这是不可能的，所以直线不存在。
………14分
命题、审稿人：谢树光 胡云华（执笔）
朱 彤 丁 蝶 施雪云