南通四县市2006届高三联合考试(数学试题)
一、选择题: 06.02.09.
1、若集合![]() ,
,![]() ,则
,则![]() 中元素个数为 ( )
中元素个数为 ( )
A、1个 B、2个 C、3个 D、4个
2、函数![]() 在区间
在区间![]() 上存在反函数的充要条件是
( )
上存在反函数的充要条件是
( )
A、![]() 或
或![]() B、
B、![]() 或
或![]() C、
C、![]() D、
D、![]()
3、有下列四个判断:
(1)若![]() ,则
,则![]()
(2)若![]() 、
、![]() 为向量,则一定有
为向量,则一定有![]()
(3)从某班54名同学中任意抽6人参加一项活动,则每位同学被抽到的概率都等于![]()
(4)设双曲线![]() 的右准线与
的右准线与![]() 轴的交点为
轴的交点为![]() ,右顶点为
,右顶点为![]() ,右焦点为
,右焦点为![]() ,则数列
,则数列![]() ,
,![]() ,
,![]() 是公比大于1的等比数列,其中正确的判断是
( )
是公比大于1的等比数列,其中正确的判断是
( )
A、(1)(2)(3) B、(2)(3)(4) C、(1)(3)(4) D、(1)(2)(4)
4、过点![]() 作圆
作圆![]() 的两切线,设两切点为
的两切线,设两切点为![]() 、
、![]() ,圆心为
,圆心为![]() ,则过
,则过![]() 、
、![]() 、
、![]() 的圆方程是
( )
的圆方程是
( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
5、若![]() 的值能被5整除,则
的值能被5整除,则![]() 的可取值的个数有
A、2个 B、3个
C、4个 D、5个
( )
的可取值的个数有
A、2个 B、3个
C、4个 D、5个
( )
6、设![]() ,
,![]() 是两条不同的直线,
是两条不同的直线,![]() ,
,![]() ,
,![]() 是不同的平面,给出如下四个命题: ( )
是不同的平面,给出如下四个命题: ( )
(1)若![]() ,则
,则![]() (2)若
(2)若![]() ,则
,则![]()
(3)若![]() ,则
,则![]() (4)若
(4)若![]() ,则
,则![]()
7、若![]() 是
是![]() 上的减函数,并且
上的减函数,并且![]() 的图象经过点
的图象经过点![]() 和
和![]() ,则不等式
,则不等式
![]() 的解集是 A、
的解集是 A、![]() B、
B、![]() C、
C、![]() D、
D、![]() ( )
( )
8、已知实数![]() 同时满足(1)
同时满足(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,则
,则![]() 的最大值是
A、
的最大值是
A、![]() B、
B、![]() C、
C、![]() D、
D、![]() ( )
( )
9、在![]() 中,若
中,若![]() ,
,![]() ,
,![]() ,则
,则![]() 的值为 ( )
的值为 ( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
10、已知椭圆![]() 与双曲线
与双曲线![]() 有相同的准线,则动点
有相同的准线,则动点![]() 的轨迹为( )
的轨迹为( )
A、椭圆的一部分 B、双曲线的一部分 C、抛物线的一部分 D、直线的一部分
11、已知![]() 为
为![]() 的边
的边![]() 的中点,
的中点,![]() 所在平面内有一点
所在平面内有一点![]() ,满足
,满足![]() ,设
,设![]() ,则
,则![]() 的值为
A、1 B、
的值为
A、1 B、![]() C、2 D、
C、2 D、![]() ( )
( )
12、已知正六棱柱的12个顶点都在一个半径为3的球面上,当正六棱柱的体积最大(柱体体积=底面积![]() 高)时,其高的值为 A、
高)时,其高的值为 A、![]() B、
B、![]() C、
C、![]() D、
D、![]() ( )
( )
二、填空题:
13、函数![]() 的单调减区间为_____________________
的单调减区间为_____________________
14、某高级中学高一有20个班级,高二有18个班级,高三有16个班级,每班都有54名学生。“神舟”报告团应邀在该校为学生作报告。现在采用分层抽样法选取324名学生代表,则高一、高二、高三出席的人数分别为_____________________
15、有甲、乙、丙三项任务,甲需要2人去完成,乙、丙各需要1人去完成,现从10人中选派4人去完成这三项任务,不同的选派方法共有______________种(用数字作答)
16、双休日,小明和小岳经过父母同意后去登山,小明以每小时![]() 公里的速度上山,以每小时
公里的速度上山,以每小时![]() 公里的速度沿原路下山,小岳上山和下山的速度都是每小时
公里的速度沿原路下山,小岳上山和下山的速度都是每小时![]() 公里,若两人在同一起点同时出发走同一条路,则先回到起点的是____________
公里,若两人在同一起点同时出发走同一条路,则先回到起点的是____________
17、已知曲线![]() 在
在![]() 处的切线恰好与抛物线
处的切线恰好与抛物线![]()
![]() 相切,则该抛物线的通径长为___________
相切,则该抛物线的通径长为___________
18、知定义在![]() 上的函数
上的函数![]() 是以2为周期的奇函数,则方程
是以2为周期的奇函数,则方程![]() 在
在![]() 上至少有__________个实数根。
上至少有__________个实数根。
三、解答题:
19、已知数列![]() 是等比数列,其首项
是等比数列,其首项![]() ,公比为2;数列
,公比为2;数列![]() 是等差数列,其首项
是等差数列,其首项![]() ,公差为
,公差为![]() ,且其前
,且其前![]() 项的和
项的和![]() 满足
满足![]()
(1)求数列![]() 的前
的前![]() 项的和
项的和![]() ;
;
(2)在数列![]() 中任取一项
中任取一项![]() ,在数列
,在数列![]()
![]() 中任取一项
中任取一项![]() ,试求满足
,试求满足![]() 的概率。
的概率。
20、如图,在矩形![]() 中,
中,![]() ,
,![]() ,此矩形沿地面上一直线滚动,在滚动过程中始终与地面垂直,设直线
,此矩形沿地面上一直线滚动,在滚动过程中始终与地面垂直,设直线![]() 与地面所成角为
与地面所成角为![]() ,矩形周边上最高点离地面的距离为
,矩形周边上最高点离地面的距离为![]() 。求(1)
。求(1)![]() 的取值范围
(2)
的取值范围
(2)![]() 的解析式
(3)
的解析式
(3)![]() 的值域
的值域

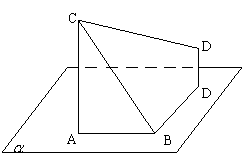 21、如图,已知线段
21、如图,已知线段![]() 在平面
在平面![]() 内,线段
内,线段![]() ,线段
,线段![]() ,
,![]() 与
与![]() 所成的角是
所成的角是![]() ,如果
,如果![]() ,
,![]() 在平面
在平面![]() 上的射影为
上的射影为![]() ,求:
,求:
(1)线段![]() 与
与![]() 所成的角
所成的角
(2)线段![]() 的长
的长
(3)二面角![]() 的余弦值
的余弦值
22、已知抛物线![]() 过椭圆
过椭圆![]() 的两焦点,且与椭圆有三个不同的公共点。
的两焦点,且与椭圆有三个不同的公共点。
(1)求抛物线方程
(2)当![]() 时,设过椭圆右焦点且与抛物线相切的直线
时,设过椭圆右焦点且与抛物线相切的直线![]() 与椭圆交于
与椭圆交于![]() 、
、![]() 两点,试求
两点,试求![]() 的面积(其中
的面积(其中![]() 是坐标原点)
是坐标原点)
23、二次函数![]() (
(![]() )的图象按向量
)的图象按向量![]() 平移后关于
平移后关于![]() 轴对称,方程
轴对称,方程![]() 的两实根为
的两实根为![]() ,且
,且![]() ,
,![]() 。
。
(1)求函数![]() 的解析式
的解析式
(2)设![]() ,若
,若![]() ,
,![]() 时,都有
时,都有![]() ,求
,求![]() 的取值范围。
的取值范围。
参考答案
一、CACADB BBDDCB
二、![]() ; 120,108,96; 2520; 小岳; 32; 5
; 120,108,96; 2520; 小岳; 32; 5
三、19、(1)解:由题意得:![]() ,由
,由![]() ,得
,得![]()
![]()
(2)解:![]() ,为1,2,4,8;
,为1,2,4,8;![]() ,为1,4,7,10
,为1,4,7,10
有序实数对![]() 共有16个,
共有16个,
当![]() 时,
时,![]() 取1,4,7共3个;当
取1,4,7共3个;当![]() 时,
时,![]() 取1,4,7共3个
取1,4,7共3个
当![]() 时,
时,![]() 取1,4,7共3个;当
取1,4,7共3个;当![]() 时,
时,![]() 取1,4共2个;
取1,4共2个;
满足题意的点共11个,所求的概率为![]()
20、(1)解:![]() 与地面所成的角,就是直线与平面所成的角的范围为
与地面所成的角,就是直线与平面所成的角的范围为![]()
(2)解:连![]() ,则
,则![]() ,过
,过![]() 作地面的垂线,垂足为
作地面的垂线,垂足为![]() ,在
,在![]() 中,
中,![]() ,
,
![]() ,
,![]()
(3)解:![]() ,
,![]() ,
,![]()
即![]() 的值域为
的值域为![]()
21、(1)![]() 在
在![]() 上的射影为
上的射影为![]() ,
,![]() ,又
,又![]()
即![]() 与
与![]() 所成的角就是
所成的角就是![]() 与
与![]() 所成的角,由题意,在
所成的角,由题意,在![]() 中,
中,![]()
即线段![]() 与
与![]() 所成的角为
所成的角为![]()
(2)在![]() 中,
中,![]() ,连
,连![]() ,可证
,可证![]() ,得
,得![]() ,
,
取![]() 中点
中点![]() ,可证
,可证![]() ,在
,在![]() 中,
中,![]() ,即
,即![]()
(3)连![]() ,在
,在![]() 中,
中,![]() ,在等腰三角形
,在等腰三角形![]() 中取
中取![]() 中点
中点![]() ,则
,则![]() ,
,
在![]() 中过
中过![]() 作
作![]() 交
交![]() 于
于![]() ,连
,连![]() ,则
,则![]() 就是面
就是面![]() 与面
与面![]() 所成的角,在
所成的角,在![]() 中,得
中,得![]() ,
,![]() ,连
,连![]() ,得
,得![]() ,在
,在![]() 中,
中,![]() ,在
,在![]() 中,
中,![]() ,
,![]() 所求角的余弦值为
所求角的余弦值为![]()
22、(1)由题意抛物线过![]() 和
和![]() 和
和![]() ,令
,令![]() ,将
,将![]() 代入得
代入得![]()
所求的抛物线方程是![]() 或
或![]()
(2)![]() ,
,![]() 抛物线方程为
抛物线方程为![]() ,
,
在抛物线![]() 上点
上点![]() 处的切线斜率为
处的切线斜率为![]() ,
,![]() 切线方程是
切线方程是![]() ,代入
,代入
![]() ,消去
,消去![]() 得:
得:![]() ,
,![]() ,
,![]() ,
,![]()
![]()
(3)在(2)中的直线![]() 的方程为
的方程为![]() ,向左平移1个单位得
,向左平移1个单位得![]() 为标准双曲线的一条渐近线,当焦点在
为标准双曲线的一条渐近线,当焦点在![]() 轴上时,
轴上时,![]() ,得
,得![]() ,又
,又![]() ,
,
当焦点在![]() 轴上时,
轴上时,![]() 。
。
23、(1)二次函数![]() 的对称轴为
的对称轴为![]() ,
,![]() 左移动1个单位后与
左移动1个单位后与![]() 轴重合,
轴重合,![]() ,
,
![]() ,令
,令![]() ,即
,即![]() 的两根分别在
的两根分别在![]() 和
和![]() 中,
中,
当![]() 时,有
时,有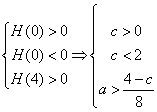 ,由
,由![]() ,由
,由
![]() ,解得
,解得![]() 或
或![]() (舍去)
(舍去)
![]()
当![]() 时,有
时,有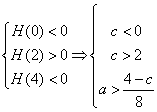 无解
无解
综上所述,![]()
(2)当![]() 时,
时,![]()
![]()
![]() 当
当![]() 时,
时,![]() ,在
,在![]() 上
上![]() 为增函数;
为增函数;
当![]() 时,
时,![]() ,在
,在![]() 上
上![]() 为减函数;
为减函数;
当![]() 时,
时,![]() ,在
,在![]() 上
上![]() 为增函数
为增函数
又![]() ,即
,即![]() ,得
,得![]()