广东省河源市连平县忠信中学高三年级数学检测题(寒假)
考试时间:120分钟 满分150分
 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷(选择题,共50分)
一.选择题:(本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1、设集合![]()
![]() <
<![]() ,
,![]() ∈
∈![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ∪
∪![]() 等于(
)A、
等于(
)A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
2、函数![]() 的图象经过四个象限的充要条件是( )
的图象经过四个象限的充要条件是( )
A、![]() <
<![]() 且
且![]() <0 B、
<0 B、![]() 且
且![]()
C、![]() <
<![]() 且
且![]() >
>![]() D、
D、![]() >
>![]() 且
且![]() >
>![]()
3、函数![]() 是(
)
是(
)
A、周期为![]() 的奇函数 B、周期为
的奇函数 B、周期为![]() 的偶函数
的偶函数
C、周期为![]() 的奇函数 D、周期为
的奇函数 D、周期为![]() 的偶函数
的偶函数
4、已知数列![]() 是等差数列,且
是等差数列,且![]() ,
,![]() ,则
,则![]() 等于( )
等于( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
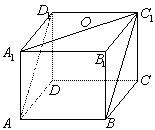 5、如图,正方体
5、如图,正方体![]() 的棱长为1,
的棱长为1,![]() 是底面
是底面
![]() 的中心,则
的中心,则![]() 到平面
到平面![]() 的距离为( )
的距离为( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
6、![]() 名同学排成两排,每排3人,其中甲排在前排的概率为( )
名同学排成两排,每排3人,其中甲排在前排的概率为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
7、在![]() 的展开式中,
的展开式中,![]() 的系数是( )
的系数是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
8、![]() 是△
是△![]() 所在平面上一点,若
所在平面上一点,若![]() ,则点
,则点![]() 是△
是△![]() 的( )
的( )
A、外心 B、内心 C、重心 D、垂心
9、若无穷等比数列![]() 满足
满足![]() ,则数列的公比
,则数列的公比![]() 为( )
为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
10、已知函数![]() 满足:①
满足:①![]() ;②在
;②在![]() 上为增函数。若
上为增函数。若![]() ,且
,且![]() ,则
,则![]() 与
与![]() 的大小关系是( )
的大小关系是( )
A、![]() B、
B、![]()
C、![]() D、 无法确定
D、 无法确定
第Ⅱ卷(非选择题,共100分)
二、填空题(本大题共4个小题,每小题5分,共20分,把答案填在题中的横线上.)
11、某校有教职工200人,男学生1000人,女学生1200人,现用分层抽样的方法从所有师生中抽取一个容量为![]() 的样本,已知从教职工中抽取的人数为10,则
的样本,已知从教职工中抽取的人数为10,则![]() = 。
= 。
12、将时间拔慢![]() 分钟,则分针转了 度,时针转了 度。
分钟,则分针转了 度,时针转了 度。
13、已知![]() ,则不等式
,则不等式![]() 的解集是 。
的解集是 。
14、已知![]() 、
、![]() 是直线,
是直线,![]() 、
、![]() 、
、![]() 是平面,给出下列命题:
是平面,给出下列命题:
①
若![]() ⊥
⊥![]() ,
,![]() ∩
∩![]() =
=![]() ,
,![]() ⊥
⊥![]() ,则
,则![]() ⊥
⊥![]() 或
或![]() ⊥
⊥![]() ;
;
②
若![]() ∥
∥![]() ,
,![]() ∩
∩![]() =
=![]() ,
,![]() ∩
∩![]() =
=![]() ,则
,则![]() ∥
∥![]() ;
;
③
若![]() 不垂直于
不垂直于![]() ,则
,则![]() 不可能垂直于
不可能垂直于![]() 内的无数条直线;
内的无数条直线;
④
若![]() ∩
∩![]() =
=![]() ,
,![]() ∥
∥![]() ,且
,且![]()
![]()
![]() ,
,![]()
![]()
![]() ,则
,则![]() ∥
∥![]() 且
且![]() ∥
∥![]() 。
。
其中正确的命题的序号是 。(注:把你认为正确的命题序号都填上)
三、解答题:(本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤.)
15、(本小题满分13分)
已知△![]() 中,角A、B、C对应的边为a、b、c,A=2B,
中,角A、B、C对应的边为a、b、c,A=2B,![]() ,求sinC的值.
,求sinC的值.
16、(本小题满分13分)
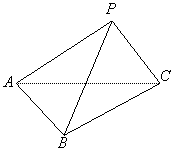 如图,三棱锥
如图,三棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,△
,△![]() 为正三角形,
为正三角形,
(Ⅰ)求证:平面![]() ⊥平面
⊥平面![]() ;
;
(Ⅱ)求棱![]() 与侧面
与侧面![]() 所成的角;
所成的角;
(Ⅲ)求点![]() 到侧面
到侧面![]() 的距离。
的距离。
17、(本小题满分13分)
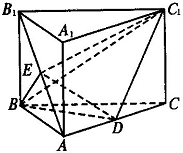
已知![]() 为正三棱柱,
为正三棱柱,![]() 是
是![]() 的中点.
的中点.
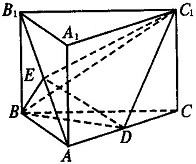 (1)证明:
(1)证明:![]() ∥平面
∥平面![]()
(2)若![]() ⊥
⊥![]() ,
,![]()
①求二面角D—BC1—C的大小;
②若E为AB1的中点,求三棱锥E—BDC1的体积。
18、(本小题满分13分)
某次有奖竞猜活动中,主持人准备了A、B两个相互独立的问题, 并且宣布:观众答对问题A可获奖金a元,答对问题B可获奖金2a元;先答哪个题由观众自由选择;只有第1个问题答对,才能再答第2个问题,否则中止答题。若你被选为幸运观众,且假设你答对问题A、B的概率分别为![]() 、
、![]() 。你觉得应先回答哪个问题才能使你获得奖金的期望较大?说明理由。
。你觉得应先回答哪个问题才能使你获得奖金的期望较大?说明理由。
19、(本小题满分14分)已知![]()
(1)
求证:过曲线 ![]()
![]()
据此证明:![]()
20.(本小题满分14分)
 已知定义域为[0,1]的函数f(x)同时满足三个条件:(1)对于任意
已知定义域为[0,1]的函数f(x)同时满足三个条件:(1)对于任意![]() ;(2)f (1)=1; (3)若x1≥0, x2≥0, x1+x2≤1,则有f (x1+x2) ≥f (x1)+f (x2)
;(2)f (1)=1; (3)若x1≥0, x2≥0, x1+x2≤1,则有f (x1+x2) ≥f (x1)+f (x2)
( I ) 试求f (0)的值;
(Ⅱ) 试求函数![]() 的最大值;
的最大值;
(Ⅲ) 试证明:当![]()
广东省河源市连平县忠信中学高三年级数学检测(寒假)答案
一. 选择题答题栏:(本大题共10小题;每小题5分,共50分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | D | C | B | D | B | A | C | D | B | A |
二、填空题(本大题共4小题,每小题5分,共20分)
11. 120;
12. ![]() 、2.5
13.
、2.5
13.![]() ≤
≤![]() ; 14 . ②④
; 14 . ②④
三、解答题:(本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤.)
15、解:∵A=2B,0<A<![]() ∴0<B<
∴0<B<![]() .
………………………1分
.
………………………1分
由![]() ,得
,得 ![]() …………………………………………3分
…………………………………………3分
∴sinA=sin2B=2sinBcosB=![]() ,cosA=cos2B=
,cosA=cos2B=![]() …………9分
…………9分
∴sinC=sin[![]() -(A+B)]= sin(A+B)=sinAcosB+cosAsinB=
-(A+B)]= sin(A+B)=sinAcosB+cosAsinB=![]() ………………12分
………………12分
解:∵A=2B,0<A<![]() ∴0<B<
∴0<B<![]() .
………………………1分
.
………………………1分
由![]() ,得
,得 ![]() …………………………………………3分
…………………………………………3分
∴sinA=sin2B=2sinBcosB=![]() ,cosA=cos2B=
,cosA=cos2B=![]() …………9分
…………9分
∴sinC=sin[![]() -(A+B)]= sin(A+B)=sinAcosB+cosAsinB=
-(A+B)]= sin(A+B)=sinAcosB+cosAsinB=![]() ………………12分
………………12分
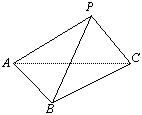 16、(Ⅰ)证明:取BC中点D,连结PD和AD,
16、(Ⅰ)证明:取BC中点D,连结PD和AD,
![]()
![]() 为正三角形
为正三角形 ![]() PD
PD![]() ,且PD=
,且PD=![]()
又![]()
![]() ,
,![]() ,
,![]()
![]() 由余弦定理可知AB=AC=
由余弦定理可知AB=AC=![]()
![]() D为BC中点
D为BC中点
![]() AD
AD![]()
![]()
![]()
又![]() PA=3 PD=
PA=3 PD=![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,
,![]() 平面
平面![]() ⊥平面
⊥平面![]()
(Ⅱ)解:由(Ⅰ)易知AD⊥平面![]() ,故
,故![]() 即为所求角
即为所求角
![]() PD=
PD=![]() ,
,![]() ,
,![]()
![]()
![]() ,
,![]()
![]() ,即PA与平面PBC所成的角为
,即PA与平面PBC所成的角为![]()
(Ⅲ)解: ![]()
![]() ,
,![]() 点B到侧面
点B到侧面![]() 的距离的
的距离的![]()
而PD=![]() ,
, ![]() =
=![]() ,
, ![]()
![]()
![]()
 17、(1)证明:连结CB1交BC1于O,连结OD.
17、(1)证明:连结CB1交BC1于O,连结OD.
∴OD∥AB1,OD在面DBC1内.∴AB1∥平面DBC1. 4分
(2)解:①OD⊥BC1,又O为BC1中点,∴DO=DC1.∴CC1=![]() .
.
过O作OM⊥BC1交BC于H,则OH=![]() ,∠HOD为所求.
,∠HOD为所求.
BH=![]() ,
,![]() ,∴cosθ=
,∴cosθ=![]() .∴θ45°. 8分
.∴θ45°. 8分
②![]() . 12分
. 12分
18.(本小题满分13分)
解:设甲先答A、B所获奖金分别为![]() 元,则有 ------------------------2分
元,则有 ------------------------2分
![]() -----5分
-----5分
![]() ---8分
---8分
![]() -----------10分
-----------10分
由于两种答序获奖金的期望相等,故先答哪个都一样。 -----------------------------12分
19.解:(1)![]() ………………………………5分
………………………………5分
(2) 由(1)知:![]() 故
故![]() 在
在![]() 是增函数…………………………7分
是增函数…………………………7分
又![]() 对于一切
对于一切![]() 恒成立.…………………………………9分
恒成立.…………………………………9分
由定理知:存在![]() ;由(1)知:
;由(1)知: ![]() ;
;
![]() ……………………12分
……………………12分
由![]() 的一般性知:
的一般性知:![]() ………14分
………14分
20.解:(Ⅰ).令![]() ,依条件(3)可得f (0+0)≥f (0)+f (0),即f (0)
,依条件(3)可得f (0+0)≥f (0)+f (0),即f (0)![]() ≤0
≤0
又由条件(1)得f (0) ≥0,则f (0)= 0;
(Ⅱ)任取0≤![]() ≤1,可知
≤1,可知![]() , 则
, 则![]()
![]()
![]() ,
,
即![]() ≥0,故
≥0,故![]()
于是当0≤x≤1时,有f (x) ≤f (1) =1,因此,当x=1时,f (x)有最大值1
(Ⅲ)证明: 当![]() 时,f (2x) ≥f (x)+f
(x)=2 f(x),∴
时,f (2x) ≥f (x)+f
(x)=2 f(x),∴![]() ,
,
显然,当![]() 时,
时,![]() ·
·![]() ·
·![]() 成立
成立
假设当![]() 时,有
时,有![]() 成立,其中k=1,2,…
成立,其中k=1,2,…
那么当![]() 时,
时,![]() ·
·![]() ·
·![]() ·
·![]() ·
·![]()
可知对于 ![]() ,总有
,总有![]() ,其中n∈N*
,其中n∈N*
此时![]() ,故
,故![]() 时,有f (x)<2x (n∈N*)
时,有f (x)<2x (n∈N*)