广东省深圳中学2005—2006学年度高三年级质量检测数学试卷
一、选择题：（本大题共10小题，每小题5分，共50分）
1．已知集合M={－1，1，2，}，集合N=
是 （ ）
A．{1，2，3} B．{1，4} C．{1} D．φ
2．
的 （ ）
A．必要非充分条件 B．充分非必要条件
C．充分必要条件 D．既非充分又非必要条件
3．在等差数列{an}中a1+ a4+ a7=39，a3+ a6+ a9=27，则数列{an}前9项和S9为 （ ）
A．66 B．99 C．144 D．297
4．若
，则 （ ）
A．a<b<c B．c<b<a C．c<a<b D．b<a<c
5．以下命题正确的是 （ ）
A．
、
都是第一象限角，若
.
B．、都是第二象限角，若
C．、都是第三象限角，若
D．、都是第四象限角，若
6．
是定义在R上的以3为周期的偶函数，且
，则方程
在区间（0，6）内解的个数的最小值是 （ ）
A．5 B．4 C．3 D．2
7．下列结论正确的是 （ ）
A．当
B．当
C．当
的最小值为2 D．当
无最大值
8．在100，101，102，…，999这些数中各位数字按严格递增（如“145”）或严格递减（如“321”顺序排列的数的个数是 （ ）
A．120 B．168 YCY C．204 D．216
9．已知k<－4，则函数
的最小值是 （ ）
A．1 B．－1 C．2k+1 D．－2k+1
|
可得n！个不同的排列，
每个排列为一行写成一个n！行的数阵，对第i行
，
i=1，2，3，…，n！.用1，2，3可成数阵如右，由于此数阵中
每一列各数之和都是12，所以，b1+b2+…+b6=－12+2×12－3×12=－24，那么，在用1，2，3，4，5形成的数阵中，b1+b2+…+b120等于（YCY）
A．－3600 B．1800 C．－1080 D．－720
二、填空题：（本大题共4小题，每小题5分，共20分.）
11．在△ABC中，角A、B的对边分别是a、b，且A=2B，则
的取值范围是
.
12．在
展开式中，含
项的系数为
，所有项系数的和为
.
13．设等比数列{an}的公比为q，前n项和为Sn，若
成等差数列，则q的值为 .
14．设奇函数在[－1，1]上是增函数，且
对所有的
时，则t的取值范围是
.
三、解答题：（本大题共6小题，共80分）
15．（满分13分）已知函数
（1）求函数的最小正周期；（2）求函数的单调减区间.
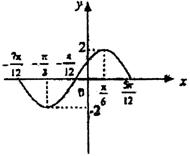
（3）画出函数
的图象，由图象研究并写出g(x)的对称轴和对称中心.
16．（满分13分）口袋里装有大小相同的卡片八张，其中三张标有数字1，三张标有数字2，二张标有数字3，第一次从口袋里任意抽取一张，放回口袋里后第二次再任意抽取一张，记第一次与第二次取到卡片上数字之和为ξ.
（1）ξ为何值时，其发生的概率最大？说明理由；（2）求随机变量ξ的期望Eξ.
17．（满分13分）
设数列
的首项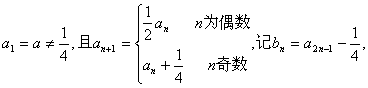
n=1，2，3，….
（1）求a2；a3； （2）判断数列{bn}是否为等比数列，并证明你的结论；
（3）求
18．（满分13分）设函数
（1）求导数
（2）对于（1）中
，若不等式
成立，求a的取值范围.
19．（满分14分）已知函数
（1）若函数的图象关于原点对称，求a的值；
（2）在（1）的条件下，解关于x的不等式
20．（满分14分）把正奇数数列{2n－1}中的数按上小下大、左小右大的原则排成如下三角形数表：
|
设
是位于这个三角形数表中从上往下数第i行，人左往右数第j个数.
（1）若amn=2005，求m，n的值；
（2）已知函数
，若记三角形数表中从上往下数第n行各数的和为bn，求数列
的前n项和Sn.
高三数学参考答案
一、选择题 1.C 2.A 3.B 4.C 5.D 6.B 7.B 8.C 9.A 10.C
二、填空题：11．（1，2） 12．60，1 13．－2 14．
三、解答题：
15．解：
…………4分
（1）
…………5分
（2）
………………8分
（3）
| x |
|
|
|
|
|
|
| － | － | 0 |
|
|
| y | 0 | －2 | 0 | 2 | 0 |
|
从图象上可以直观看出，此函数有一个对称中心
，无对称轴. ……13分
16．解：（1）依题意，随机变量ξ的取值是2、3、4、5、6 …………1分
因为
，
; 
所以，当ξ=4时，其发生的概率
最大. …………10分
（2）
…………13分
17．解：（1）
； …………4分
（2）∵
…………6分
所以
猜想：{bn}是公比为
的等比数列. …………8分
证明如下：因为
所以{bn}是首项为
的等比数列. …………10分
（3）
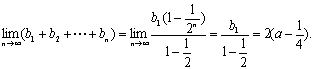…………13分
18．解：（1）∵函数
∴
…………2分
令
则
…………4分
∴
有两个不相同的实数根 
）
则当
∴有两个不同的极值点
处取得极大值，在x2处取得极小值.……6分
（2）∵
的两个根
∴
……………………7分
∴
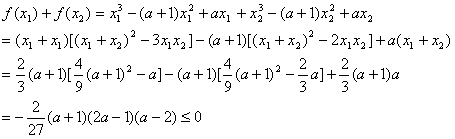
………………12分
又∵a>1 ∴a≥2 ………………13分
19．解；（1）因为函数的图象关于原点对称
∴
…………2分
有
化简得
又∵
…………6分
（2）由（1）知：
…………9分
∵
①当
无解 …………10分
②当－1<m<1时,解不等式
…13分
③当
…………14分
20．解：（Ⅰ）∵三角形数表中前m行共有1+2+3+…+m=
个数，
∴第m行最后一个数应当是所给奇数列中的第项.
故第m行最后一个数是
…………2分
因此，使得
的m是不等式
的最小正整数解.
由
∴
于是，第45行第一个数是442+44－1+2=1981
∴
…………6分
（Ⅱ）∵
故 
…………8分
∵第n行最后一个数是n2+n－1，且有n个数，若将n2+n－1看成第n行第一个数，则
第n行各数成公差为－2的等差数列，故 
∴
…………10分
故 
∵
两式相减得：
…………12分
∴
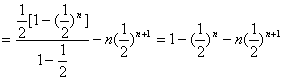
…………14分