杭州西湖高级中学高三3月月考数学试卷(理科卷)
一、选择题(每小题所给的四个选项中,只有一个符合题目要求,每小题5分,共50分)
1.已知函数![]() 的图像经过点
的图像经过点![]() ,则常数
,则常数![]() 的值为 ( )
的值为 ( )
A.2
B.4 C.![]() D.
D. ![]()
2.函数![]() 的最小正周期是 ( )
的最小正周期是 ( )
A.![]() B.
B. ![]() C.
C.![]() D.
D.![]()
3.已知三个力![]() ,
,![]() ,
,![]() 同时作用于某物体上一点,为使物体保持平衡,现加上一个力
同时作用于某物体上一点,为使物体保持平衡,现加上一个力![]() ,则
,则![]() 等于 ( )
等于 ( )
A.(-1,-2) B.(1,-2) C.(-1,2) D.(1,2)
4.![]() 为等差数列
为等差数列![]() 的前n项和,S9=-36,S13=-104,等比数列
的前n项和,S9=-36,S13=-104,等比数列![]() 中,
中, ![]() ,
,![]() ,则
,则![]() 等于 ( )
等于 ( )
A.![]() B.-
B.-![]() C.±
C.± ![]() D.无法确定
D.无法确定
5.![]() 是
是![]() 的 ( )
的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.不充分不必要条件
6.函数![]() 的图象无论经过平移还是关于某条直线对称翻折后仍不能与
的图象无论经过平移还是关于某条直线对称翻折后仍不能与![]() 的图象重合,则
的图象重合,则![]() 是 ( )
是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.以椭圆![]() 的右焦点为圆心,且与双曲线
的右焦点为圆心,且与双曲线![]() 的渐近线相切的圆的方程是 ( )
的渐近线相切的圆的方程是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
8.如果一个点是一个指数函数的图象与一个对数函数的图象的公共点,那么称这个点为“好
点”。在下面五个点M(1,1),N(1,2),P(2,1),Q(2,2),G(2,![]() )中,“好
)中,“好
点”的个数为( ) A.0个 B.1个 C.2个 D.3个
9.已知双曲线的两个焦点为![]() ,
,![]() ,P是此双曲线上的一点,且
,P是此双曲线上的一点,且![]() ,
, ![]() ,则该双曲线的方程是
( )
,则该双曲线的方程是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.由正方体的八个顶点中的两个所确定的所有直线中,取出两条,这两条直线是异面直线的概率为 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
二、填空题(本大题共4小题,每小题4分,共16分,把答案填在题中横线上)
11.若圆锥曲线![]() 的焦距与k无关,则它的焦点坐标是__________.
的焦距与k无关,则它的焦点坐标是__________.
12.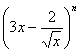 的展开式中第9项是常数项,n的值是
的展开式中第9项是常数项,n的值是
13.若点A(1,2)和B(1,1)在直线3x-y+m=0的异侧,则m的取值范围是______________
14.椭圆![]() +
+![]() =1(a>b>0)上两点A,B与中心O的连线互相垂直,则
=1(a>b>0)上两点A,B与中心O的连线互相垂直,则![]() =
=
三.解答题:(每小题14分,共84分.解答应写出文字说明,证明过程或演算步骤)
15. 已知向量![]() =(sinB,1-cosB),且与向量
=(sinB,1-cosB),且与向量![]() (2,0)所成角为
(2,0)所成角为![]() ,其中A, B, C是⊿ABC的内角.
,其中A, B, C是⊿ABC的内角.
(1)求角B的大小;
(2)求sinA+sinC的取值范围.
16.有红蓝两粒质地均匀的正方体形状骰子,红色骰子有两个面是8,四个面是2,蓝色骰子有三个面是7,三个面是1,两人各取一只骰子分别随机投掷一次,所得点数较大者获胜. ⑴分别求出两只骰子投掷所得点数的分布列及期望;⑵投掷蓝色骰子者获胜的概率是多少?
17.已知抛物线![]() 上两定点A、B分别在对称轴两侧,F为焦点,且
上两定点A、B分别在对称轴两侧,F为焦点,且![]() ,在抛物线的AOB一段上求一点P,使
,在抛物线的AOB一段上求一点P,使![]() 最大,并求面积最大值。
最大,并求面积最大值。
18.已知函数f(x)=(x2+![]() )(x+a)(a
)(x+a)(a![]() R)
R)
(1)若函数f(x)的图象上有与x轴平行的切线,求a的范围;
(2)若![]() (-1)=0,(I)求函数f(x)的单调区间;(II)证明对任意的x1、x2
(-1)=0,(I)求函数f(x)的单调区间;(II)证明对任意的x1、x2![]() (-1,0),不等式f(x1)-f(x2)<
(-1,0),不等式f(x1)-f(x2)<![]() 恒成立。
恒成立。
19.双曲线的中心是原点O,它的虚轴长为![]() ,相应于焦点F(c,0)(c>0)的准线l与x轴交于点A,且 OF = 3 OA 。过点F的直线与双曲线交于P、Q两点。
,相应于焦点F(c,0)(c>0)的准线l与x轴交于点A,且 OF = 3 OA 。过点F的直线与双曲线交于P、Q两点。
(Ⅰ)求双曲线的方程及离心率;(Ⅱ)若![]() =0,求直线PQ的方程。
=0,求直线PQ的方程。
20.设A(x1,y1),B(x2,y2)是函数f(x)=![]() 的图象上任意两点,且
的图象上任意两点,且![]() ,已知点M的横坐标为
,已知点M的横坐标为![]() .
.
(1) 求证:M点的纵坐标为定值;
(2) 若Sn=f(![]() ∈N*,且n≥2,求Sn;
∈N*,且n≥2,求Sn;
(3) 已知an=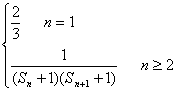 ,其中n∈N*.
,其中n∈N*.
Tn为数列{an}的前n项和,若Tn<λ(Sn+1+1)对一切n∈N*都成立,试求λ的取值范围.
参考答案(理科卷)
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | D | B | D | C | A | D | A | C | C | B |
二、填空题
11.![]() 12. 12 13.(-2,-1) 14.
12. 12 13.(-2,-1) 14. ![]()
三.解答题
15. 解:(1)∵![]() =(sinB,1-cosB)
, 且与向量
=(sinB,1-cosB)
, 且与向量![]() (2,0)所成角为
(2,0)所成角为![]()
∴![]() ∴tan
∴tan![]()
(2)由(1)得![]()
∵![]() ∴
∴![]() ∴
∴![]()
当且仅当![]()
16.(理科) 解:⑴红色骰子投掷所得点数为![]() 是随即变量,其分布如下:
是随即变量,其分布如下:

![]() 8 2
8 2
P ![]()
![]()
E![]() =8·
=8·![]() +2·
+2·![]() =4
=4
蓝色骰子投掷所得点数![]() 是随即变量,其分布如下:
是随即变量,其分布如下:

![]() 7 1
7 1
P ![]()
![]()
E![]() =7·
=7·![]() +1·
+1·![]() =4
=4
⑵∵投掷骰子点数较大者获胜,∴投掷蓝色骰子这若获胜,则投掷后蓝色骰子点数为7,
红色骰子点数为2,∴投掷蓝色骰子获胜概率是![]() =
=![]() ·
·![]() =
=![]()
17. 解:P ![]() ,最大
,最大![]() =
=![]()
18.解:![]() ,
,![]()
⑴![]() 函数
函数![]() 的图象有与
的图象有与![]() 轴平行的切线,
轴平行的切线,![]() 有实数解
有实数解
![]() ,
,![]() ,
,
所以![]() 的取值范围是
的取值范围是![]()
⑵![]() ,
,![]() ,
,![]() ,
,![]()
(Ⅰ)由![]() 或
或![]() ;由
;由![]()
![]() 的单调递增区间是
的单调递增区间是![]() ;单调减区间为
;单调减区间为![]()
(Ⅱ)易知![]() 的最大值为
的最大值为![]() ,
,![]() 的极小值为
的极小值为![]() ,又
,又![]()
![]() 在
在![]() 上的最大值
上的最大值![]() ,最小值
,最小值![]()
![]() 对任意
对任意![]() ,恒有
,恒有![]()
19.(Ⅰ)由题意,设曲线的方程为![]() = 1(a>0b>0)
= 1(a>0b>0)
由已知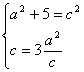 解得a =
解得a =![]() ,c = 3
,c = 3
所以双曲线的方程这![]() = 1离心率e =
= 1离心率e =![]() ……………………………5分
……………………………5分
(Ⅱ)由(Ⅰ)知A(1,0),F(3,0),
当直线PQ与x轴垂直时,PQ方程为x = 3 .此时,![]() ≠0,应舍去.
≠0,应舍去.
当直线PQ与x轴不垂直时,设直线PQ的方程为y = ( x – 3 ).
由方程组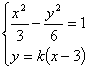 得
得 ![]()
由一过点F的直线与双曲线交于P、Q两点, 则![]() -2≠0,即k≠
-2≠0,即k≠![]() ,
,
由于△=36![]() -4(
-4(![]() -2)(9
-2)(9![]() +6) =48(
+6) =48(![]() +1)>0即k∈R.
+1)>0即k∈R.
∴k∈R且k≠![]() (*)
(*)
设P(![]() ,
,![]() ),Q(
),Q(![]() ,
,![]() ),则
),则
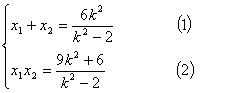
由直线PQ的方程得![]() = k(
= k(![]() -3),
-3),![]() = k(
= k(![]() -3)
-3)
于是![]()
![]() =
=![]() (
(![]() -3)(
-3)(![]() -3)=
-3)=![]() [
[![]()
![]() -3(
-3(![]() +
+![]() )+ 9] (3)
)+ 9] (3)
∵![]() = 0, ∴(
= 0, ∴(![]() -1,
-1,![]() )·(
)·(![]() -1,
-1,![]() )= 0
)= 0
即![]()
![]() -(
-(![]() +
+![]() )+ 1 +
)+ 1 + ![]()
![]() = 0
(4)
= 0
(4)
由(1)、(2)、(3)、(4)得
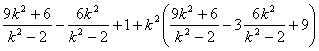 = 0
= 0
整理得![]() =
=![]() ∴k =
∴k =![]() 满足(*)
满足(*)
∴直线PQ的方程为x - ![]() -3 = 0或x +
-3 = 0或x +![]() -3 = 0
-3 = 0
20.(1)证明:∵![]() ∴M是AB的中点.设M点的坐标为(x,y),
∴M是AB的中点.设M点的坐标为(x,y),
由![]() (x1+x2)=x=
(x1+x2)=x=![]() ,得x1+x2=1,则x1=1-x2或x2=1-x1.
,得x1+x2=1,则x1=1-x2或x2=1-x1.
而y=![]() (y1+y2)=
(y1+y2)= ![]() [f(x1)+f(x2)] =
[f(x1)+f(x2)] =![]() (
(![]() +log2
+log2![]()
=![]() (1+log2
(1+log2![]() =
=![]() (1+log2
(1+log2![]()
=![]() (1+log2
(1+log2![]()
∴M点的纵坐标为定值![]() .
.
(2)由(1)知x1+x2=1,f(x1)+f(x2)=y1+y2=1,
Sn=f(![]()
Sn=f(![]() ,
,
两式相加得:
2Sn=[f(![]() )+[f(
)+[f(![]() )+…+[f(
)+…+[f(![]() )
)
=![]()
∴Sn=![]() (n≥2,n∈N*).
(n≥2,n∈N*).
(2)当n≥2时,an=![]()
Tn=a1+a2+a3+…+an=![]() [(
[(![]() )
)
=![]() (
(![]()
由Tn<λ(Sn+1+1)得![]() <λ·
<λ·![]()
∴λ>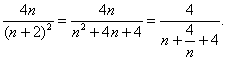
∵n+![]() ≥4,当且仅当n=2时等号成立,
≥4,当且仅当n=2时等号成立,
∴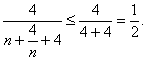
因此λ>![]() ,即λ的取值范围是(
,即λ的取值范围是(![]() +∞)
+∞)