08届高考理科数学第二次质量检测试题
注意事项：
1、本试卷分第I卷（选择题）第II卷（非选择题）两部分，共150分，考试时间20分钟。
2、请将第I卷选择题的答案用2B铅笔填涂在答题卡上，第II卷在各题后直接作答。
第I卷
一、选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的）
1．若集合
。，那么
A．
B．
． C．
D．
2．已知复数
A．2 B．－2 C．1/2 D．－1/2
3．已知
A．
B．
C．
D．
4．已知不等式
对任意正实数x，y恒成立．则正实数a的最小值为
A．2 B．4 C．6 D．8
5．已知
是不共线的向量
那么A、B、C三点共线的充要条件是
A．
B．
C．
D．
6．若P是两条异面直线m，n外的任意一点，则
A．过点P有且仅有一条直线与m，n都平行
B．过点P有且仅有一条直线与m，n都垂直
C．过点P有且仅有一条直线与m，n都相交
D．过点P有且仅有一条直线与m，n都异面
7．已知点F（1，0），直线
，点B是L上的动点，过点B平行于x轴的直线与线段BF的垂直平分线交于点M，则点M的轨迹是
A．圆 B．抛物线 C．椭圆 D．双曲线
8．若圆
。上至少有三个不同的点到直线
的距离为
，则直线z的倾斜角的取值范围是
A．
B．
C．
D．
9．已知
的前n项和
A．67 B．65 C．6l D．56
10．设函数
若对任意x∈R都有
成立，则
的最小为
A．4 B．2 C．1 D．土2
11．函数
的图象是两条直线的一部分，如图所示，其定义域为
，则不等式
的解集为
A．{x—1≤x≤1且x≠0} B．{x一1≤x<0}
C．{x —l≤x<0或1/2<x≤一1} D．{x一1≤x<一1/2或0<x≤1}
12．已知椭圆
，直线
交椭圆于A、B两点，△AOB面积为S（O为原点），则函数
的奇偶性为
A．奇函数 B．偶函数
C．既不是奇函数，也不是偶函数 D．奇偶性与a、b有关
第Ⅱ卷
二、填空题（本大题共4小题，每小题5分，共20分，把答案填在题中的横线上）
13．若
的展开式的各项系数之和为—32，那么展开式的常数项为
。
14．从8盆不同的鲜花中选出4盆排成一排，其中甲、乙两盆有且仅有一盆展出的不同摆法种数 用数字作回答）
15．在坐标平面内，由不等式组
所确定的平面区域的面积为
。
16．在正三棱锥P—ABC中，PC垂直于面PAB，PC=，则过点P、A、B、C的球的体积为
．
三、解答题（本大题有6个小题，共70分．解答应写出文字说明。证明过程或演算步骤）
17．（本小题满分10分）
已知A、B、C是△ABC的内角，向量
，且
（1）求角A；
（2）若
．求
18．（本小题满分12分）
袋中有4个黑球，3个白球，2个红球，从中任取2个球．已知每取到一个黑球得0分，每取到一个白球得1分，每取到一个红球得2分．
（1）求取到2个球的分数和不为0的概率；
（2）用表示任取2个球的分数和，求的分布列和数学期望．
19．（本小题满分12分）
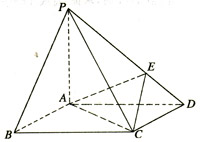如图，在底面是四棱锥P—ABCD中，
，点E在PD上，且PE：ED=2：1
（1）证明：PA⊥平面ABCD；
（2）求二面角P—AC—E的大小．
20．（本小题满分12分）
已知函数
（1）若在x∈（0，1]上是增函数，求a的取值范围；
（2）求在区间（0，1]上的最大值．
21．（本小题满分12分）
已知双曲线方程
的一条渐近线为
，其左焦点到右准线的距离为
（1）求此双曲线的方程；
（2）过点A（
，0）作斜率不为0的直线，交双曲线的右支于点C，交双曲线的左支于点D，过点D作x轴的垂线，交双曲线于点M，证明直线MC过定点．
22．（本小题满分12分）
数列
的首项
= 1，且对任意n∈N，与
恰好为方程
的两个个根．
（1）求数列和数列
的通项公式；
（2）求数列的前n项和
。
参考答案
一、选择题：
l——5 C A C B D 6——10 B B B A B 1l——12 D B
二、填空题：
13．90 14．960
15．16
16．
三、解答题：
17．（1）
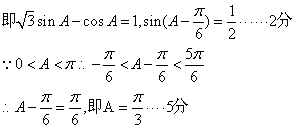
（2）由题意知，整理得
，即
或
即时，使
18．（1）设两球分数之和为0的事件A
分布列是
|
| 0 | 1 | 2 | 3 | 4 |
| P |
|
|
|
|
|
19．（1）证明：因为底面ABCD是菱形，
，
所以AB=AD=AC=a ……1分
在
，
同理，
． 
……4分
（2）
作
7分
20．（1）
，∴在
是增函数，有
，即
，
在
在是增函数，且
∴当
时，
在上也有
∴
为所求 6分
（2）由（1）知时，在是增函数，
∴当时，
8分
当
时，令
，得
∴当
时，，当
时，
10分
当时，
11分
故对，当时，
，
当时，
12分
21．（1）由已知得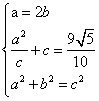
解得
……．3分
即双曲线方程为丁
……4分
（2）设直线CD的方程为
直线MC的方程为
，
设C
D
则由已知得M
由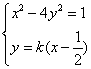
消去y整理得
①………6分
由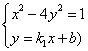
消去y整理得
②……8分
由题意可知
．
是方程①的根，也是方程②的根
③ ④
由③解得
带入④化简整理可得
………10分
即直线MC的方程为：
则直线MC恒过（2．0）点………12分
22．（1）由题意
（2）
