韶关市2006届高三第二次调研考试
数 学
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。第Ⅰ部分1至2页,第Ⅱ部分3至8页。共150分。考试时间120分钟。
参考公式:
如果事件A、B互斥,那么![]() .
.
如果事件A、B相互独立,那么![]() .
.
第一部分 选择题(共50分)
注意事项:每小题选出正确答案后,用钢笔或圆珠笔将答案填在第二部分相应的表格内。
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项符合题目要求的.
(1)复数![]() =
=
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(2)设函数![]() ,如果
,如果![]() ,则
,则![]() 的最小值为
的最小值为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(3)已知集合![]() ,集合
,集合![]()
则![]()
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(4)方程![]() 的根所在的区间是
的根所在的区间是
(A)(1,2) (B)(![]() ,
,![]() ) (C)(
) (C)(![]() ,
,![]() ) (D)(
) (D)(![]() ,
,![]() )
)
(5)下列图象中,有一个是函数![]() 的导函数
的导函数![]() 的图象,
的图象,
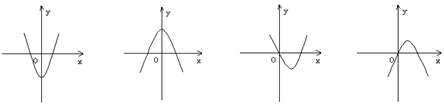
则![]()
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]() 或
或![]()
(6)设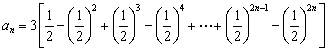 ,则数列
,则数列![]() 是一个
是一个
(A) 无限接近1的递增数列 (B) 是一个各项为0的常数列
(C) 无限接近2的递增数列 (D) 是一个无限接近![]() 的递增数列
的递增数列
(7)已知定义在R上的偶函数f(x)的单调递减区间为[0,+∞![]() ,则不等式
,则不等式
![]() 的解集是
的解集是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(8)已知双曲线![]() 的右顶点为
的右顶点为![]() ,而
,而![]() 是双曲线同一支上的两点,如果
是双曲线同一支上的两点,如果![]() 是正三角形,则
是正三角形,则
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
(9)已知球面上有三点![]() ,
,![]() ,球心到平面
,球心到平面![]() 的距离为
的距离为![]() ,则球的半径为
,则球的半径为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(10)椭圆![]() 上有
上有![]() 个不同的点
个不同的点![]() ,椭圆的右焦点为
,椭圆的右焦点为![]() ,数列
,数列![]() 是公差大于
是公差大于![]() 的等差数列,则n的最大值为
的等差数列,则n的最大值为
(A) 198 (B) 199 (C) 200 (D) 201
韶关市2006届高三第二次调研考试
数 学
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。第Ⅰ部分1至2页,第Ⅱ部分3至8页。共150分。考试时间120分钟。
第二部分 非选择题(共100分)
选择题答案
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
注意事项:
1、第Ⅱ部分共6页,用钢笔或圆珠笔将答案直接写在试卷上。
2、答卷前将密封线内的项目填写清楚。
| 题号 | 一 | 二 | 三 | 总 分 | ||||||||
| 1—10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | ||
| 分数 | ||||||||||||
二、填空题:本大题共4小题,每小题5分,共20分.有两个空的小题,前一个空3分,后一个空2分.
(11)在二项展开式![]() 中,
中,
![]() ______________.
______________.
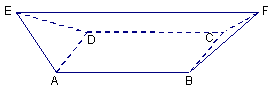 (12)如图,在多面体
(12)如图,在多面体![]() 中,
中,
已知四边形![]() 是边长为
是边长为![]() 的正方
的正方
形,且![]() 和
和![]() 为正三角形,
为正三角形,
![]() ,
,![]() ,则
,则![]() 到平面
到平面
![]() 的距离为_______________.
的距离为_______________.
(13)已知数列![]() 的前
的前![]() 项和
项和![]() ,则
,则![]() ___________;
___________;![]() __________.
__________.
(14)若圆![]() :
: ![]() 与
与![]() 轴相切,则
轴相切,则![]() _______________;圆
_______________;圆![]() 关于直线
关于直线![]() 对称的圆
对称的圆![]() 的方程是____________________.
的方程是____________________.
三、解答题
(15)(本小题满分12分)
在⊿![]() 中,内角
中,内角![]() 的对边分别是
的对边分别是![]() ,已知
,已知![]() .
.
(Ⅰ)试判断⊿![]() 的形状;
的形状;
(Ⅱ)若![]() 求角B的大小.
求角B的大小.
(16)(本小题满分14分)
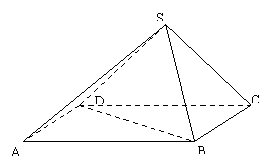
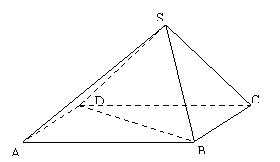
如图所示,在四棱锥![]() 中,底面
中,底面![]() 是矩形,侧面
是矩形,侧面![]() 底面
底面![]() ,且
,且![]() ,
,![]() 。
。
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)设![]() ,
,![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求
,求![]() 的取值范围.
的取值范围.
(17)(本小题满分12分)
假设某批产品的正品率为![]() ,某检验员在检验这批产品时,把正品检验为正品的概率为
,某检验员在检验这批产品时,把正品检验为正品的概率为![]() ,把次品检验为次品的概率为
,把次品检验为次品的概率为![]() .设“该检验员在检验这批产品时恰好将正品都检验为正品, 把次品都检验为次品”为事件A, 求事件A的概率
.设“该检验员在检验这批产品时恰好将正品都检验为正品, 把次品都检验为次品”为事件A, 求事件A的概率![]() .
.
(18)(本小题满分14分)
在平面直角坐标系上,设不等式组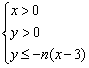 所表示的平面区域为
所表示的平面区域为![]() ,记
,记![]() 内的整点(即横坐标和纵坐标均为整数的点)的个数为
内的整点(即横坐标和纵坐标均为整数的点)的个数为![]() .
.
(Ⅰ)求![]()
(Ⅱ)求数列![]() 的通项公式
的通项公式![]() 和前
和前![]() 项和
项和![]() ;
;
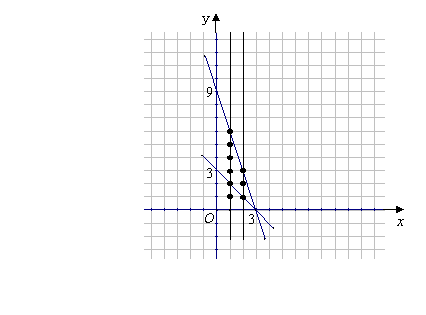 (Ⅲ)设数列
(Ⅲ)设数列![]() 的前
的前![]() 项和为
项和为![]() ,求
,求
![]()
(19)(本小题满分14分)
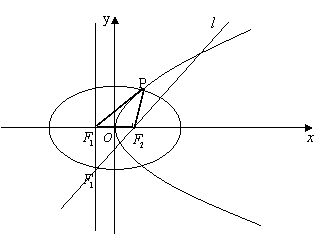
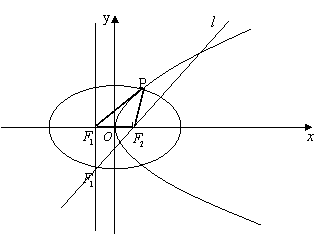
设抛物线![]()
![]() 的准线与
的准线与![]() 轴交于
轴交于![]() ,焦点为
,焦点为![]() ;以
;以![]() 为焦点,离心率
为焦点,离心率![]() 的椭圆
的椭圆![]() 与抛物线
与抛物线![]() 的一个交点为
的一个交点为![]() .
.
(Ⅰ)当![]() 时,直线
时,直线![]() 经过椭圆
经过椭圆![]() 的右焦点
的右焦点![]() ,与抛物线
,与抛物线![]() 交于
交于![]() ,如果弦长
,如果弦长![]() 等于三角形
等于三角形![]() 的周长,求直线
的周长,求直线![]() 的斜率.
的斜率.
(Ⅱ)求最小实数![]() ,使得三角形
,使得三角形![]() 的边长是自然数.
的边长是自然数.
(20)(本小题满分14分)
(Ⅰ)已知函数:![]() 求函数
求函数![]() 的最小值;
的最小值;
(Ⅱ)证明:![]() ;
;
(Ⅲ)定理:若![]() 均为正数,则有
均为正数,则有![]() 成立
成立
(其中![]() .请你构造一个函数
.请你构造一个函数![]() ,证明:
,证明:
当![]() 均为正数时,
均为正数时,![]() .
.
韶关市2006届高三第二次调研考试
数学试题参考答案及评分标准
一、选择题:
(1)A(2)D(3)A(4)B(5)B(6)A(7)B(8)D(9)D(10)C
二、填空题:
(11)512(12)![]() (13)2,18(14)1,
(13)2,18(14)1,![]()
三、解答题:
(15)解:(Ⅰ)由余弦定理得:
![]() …………………..2分
…………………..2分
故:![]() ……………………………………………………………5分
……………………………………………………………5分
所以⊿![]() 是以角C为直角的直角三角形。………………………………6分
是以角C为直角的直角三角形。………………………………6分
另解:由正弦定理得![]()
![]()
![]()
即![]() 从而有
从而有 ![]()
(Ⅱ)![]() …………..8分
…………..8分
故![]() 同理
同理 ![]() ……………………………………10分
……………………………………10分
在![]() ⊿
⊿![]() 中,
中,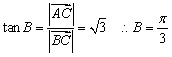 .………………………….12分
.………………………….12分
(16)(Ⅰ)证明:在![]() 中,
中,![]() ,
,![]()
![]() 即
即![]()
![]() 底面
底面![]() 是矩形
是矩形 ![]() ……………3分
……………3分
又![]() 平面
平面![]() 平面
平面![]()
![]() 面
面![]()
![]()
![]() 平面
平面![]() …………………………...……..6分
…………………………...……..6分
![]() 平面
平面![]()
![]() 平面
平面![]() 平面
平面![]() .……………………….7分
.……………………….7分
(Ⅱ)由(Ⅰ)知,![]() 平面
平面![]()
![]() 是
是![]() 在平面
在平面![]() 上的射影
上的射影
![]() 就是
就是![]() 与平面
与平面![]() 所成的的角,即
所成的的角,即![]() …………………….10分
…………………….10分
那么![]()
![]()
![]() ………………………….12分
………………………….12分
由![]() 得
得![]() . ……………………………………...………14分
. ……………………………………...………14分
(17)解:设事件![]() “正品”
“正品” ![]() “次品”
“次品”
![]() “正品检验为正品”
“正品检验为正品” ![]() “次品检验为次品” …………4分
“次品检验为次品” …………4分
则:![]() ,
,![]() ,
,![]() ,
,![]() ……...…6分
……...…6分
![]() ……………………………………………………………….9分
……………………………………………………………….9分
故![]()
![]()
![]() …. 11分
…. 11分
答:事件A的概率为![]() . ………………………………………12分
. ………………………………………12分
(18)解:(Ⅰ)![]() …………………………………………………3分
…………………………………………………3分
(Ⅱ)由![]() 得
得![]() ………………………………4分
………………………………4分
![]() 内的整数点在直线
内的整数点在直线![]() 和
和![]() 上 …………………………………………5分
上 …………………………………………5分
设直线![]() 与直线
与直线![]() 的交点分别为
的交点分别为![]() ,则
,则![]()
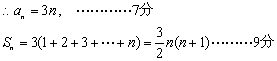 . ……………………………
. ……………………………
(Ⅲ)![]() …………………………………………………11分
…………………………………………………11分
![]() ……………………………13分
……………………………13分
故: ![]() ……………………………………………………………………………14分
……………………………………………………………………………14分
(19)解:(Ⅰ)已知![]() ,
,![]()
故椭圆方程为![]() ,即
,即 ![]() .依题意知直线
.依题意知直线![]() 存在斜率,设
存在斜率,设![]() :
:![]()
联立![]() 得
得 ![]() …………………………3分
…………………………3分
![]() 直线
直线![]() 与抛物线
与抛物线![]() 有两个交点,
有两个交点,![]()
设![]() ,弦
,弦![]() 的中点
的中点![]() ,由韦达定理得
,由韦达定理得
![]() …………………………………………..5分
…………………………………………..5分
则
![]()
![]()
![]() ………………………………………8分
………………………………………8分
三角形![]() 的周长
的周长![]() 由
由 ![]() 解得
解得 ![]() . ………9分
. ………9分
(Ⅱ)设椭圆长半轴为![]() ,半焦距为
,半焦距为![]() ,由题设有
,由题设有![]() .
.
 又设
又设![]() ,有
,有![]()
设![]() ,对于抛物线
,对于抛物线![]() ,
,![]() ;
;
对于椭圆![]() ,
,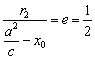 ,
,
即![]() …………………..12分
…………………..12分
由![]() 解得
解得 ![]()
![]() 从而
从而 ![]()
因此,三角形![]() 的边长分别是
的边长分别是![]() .…………………………………13分
.…………………………………13分
使得三角形![]() 的边长是连续的自然数的最小实数
的边长是连续的自然数的最小实数![]() . …….…………14分
. …….…………14分
(20)解:(Ⅰ)令![]()
得![]() ……………………………………2分
……………………………………2分
当![]() 时,
时,![]()
![]() 故
故![]() 在
在![]() 上递减.
上递减.
当![]() 故
故![]() 在
在![]() 上递增.
上递增.
所以,当![]() 时,
时,![]() 的最小值为
的最小值为![]() ….……………………………………..4分
….……………………………………..4分
(Ⅱ)由![]() ,有
,有![]() 即
即![]()
故 ![]() .………………………………………5分
.………………………………………5分
(Ⅲ)证明:要证: ![]()
只要证:![]()
设![]()
![]() …………………7分
…………………7分
则![]()
令![]() 得
得![]() …………………………………………………….8分
…………………………………………………….8分
当![]()
![]() 时,
时,![]()
![]()
![]()
故![]() 上递减,类似地可证
上递减,类似地可证![]() 递增
递增
所以![]() 的最小值为
的最小值为![]() ………………10分
………………10分
而![]() =
=![]()
=![]()
=![]()
由定理知: ![]() 故
故![]()
![]()
故![]()
即: ![]() .…………………………..14分
.…………………………..14分